The ratio of the density of 3 kinds of petrol P1, P2 and P3 is 9 : 7 : 5. The density of P1 is 18 gm/cc and P1, P2 and P3 are mixed in the ratio of 6 : 5 : 4 by weight. If a litre of P3 cost ₹ 40, then find the cost of P3 in 450 kg of mixture of P1, P2 and P3 :
₹ 380
₹ 480
₹ 355
₹ 448
The correct Answer is:B
To solve the problem step by step, we will break it down into manageable parts:
Step 1: Understand the given ratios and densities
The ratio of the densities of petrol P1, P2, and P3 is given as 9:7:5. We know that the density of P1 is 18 gm/cc.
Step 2: Calculate the densities of P2 and P3
Using the ratio of densities:
- Density of P1 = 9 parts = 18 gm/cc
- Density of P2 = (7/9) * 18 gm/cc = 14 gm/cc
- Density of P3 = (5/9) * 18 gm/cc = 10 gm/cc
Step 3: Determine the total weight of the mixture
The petrols are mixed in the ratio of 6:5:4 by weight. The total parts in this mixture = 6 + 5 + 4 = 15 parts.
Step 4: Calculate the weight of each type of petrol in the mixture
Given the total weight of the mixture = 450 kg:
- Weight of P1 = (6/15) * 450 kg = 180 kg
- Weight of P2 = (5/15) * 450 kg = 150 kg
- Weight of P3 = (4/15) * 450 kg = 120 kg
Step 5: Convert the weight of P3 to volume
We know the density of P3 is 10 gm/cc. To convert the weight of P3 to volume:
- Weight of P3 = 120 kg = 120,000 gm
- Volume of P3 = Weight / Density = 120,000 gm / 10 gm/cc = 12,000 cc
Step 6: Convert volume from cc to liters
Since 1 liter = 1000 cc:
- Volume of P3 in liters = 12,000 cc / 1000 = 12 liters
Step 7: Calculate the cost of P3
The cost of P3 is given as ₹40 per liter:
- Total cost of P3 = 12 liters * ₹40/liter = ₹480
Final Answer
The cost of P3 in 450 kg of the mixture of P1, P2, and P3 is ₹480.
---
The ratio of the densities of petrol P1, P2, and P3 is given as 9:7:5. We know that the density of P1 is 18 gm/cc.
Using the ratio of densities:
- Density of P1 = 9 parts = 18 gm/cc
- Density of P2 = (7/9) * 18 gm/cc = 14 gm/cc
- Density of P3 = (5/9) * 18 gm/cc = 10 gm/cc
The petrols are mixed in the ratio of 6:5:4 by weight. The total parts in this mixture = 6 + 5 + 4 = 15 parts.
Given the total weight of the mixture = 450 kg:
- Weight of P1 = (6/15) * 450 kg = 180 kg
- Weight of P2 = (5/15) * 450 kg = 150 kg
- Weight of P3 = (4/15) * 450 kg = 120 kg
We know the density of P3 is 10 gm/cc. To convert the weight of P3 to volume:
- Weight of P3 = 120 kg = 120,000 gm
- Volume of P3 = Weight / Density = 120,000 gm / 10 gm/cc = 12,000 cc
Since 1 liter = 1000 cc:
- Volume of P3 in liters = 12,000 cc / 1000 = 12 liters
The cost of P3 is given as ₹40 per liter:
- Total cost of P3 = 12 liters * ₹40/liter = ₹480
The cost of P3 in 450 kg of the mixture of P1, P2, and P3 is ₹480.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The ratio of density of 3 kinds of petrol P1,P2 and P3 is 9:7:5. The density of P1 is 18 gm/ cc and P1,P2,P3d are mixed in the ratio of 6:5:4 by weight. If a litre of P3 cost Rs. 40, then find the cost of P3 in 450 kg of mixture of P1,P2 and P3
ARs. 380BRs. 480CRs. 355DRs. 448When equal volumes of three liquids of densities p1,p2,p3 are mixed then the resultant density of the mixture will be:
Ap1+p2+p33Bp1+p2+p36Cp21+p22+p236Dp1+p2+p3Consider the planes P1:2x–y+2z=1,P2:x+2y–zand=2
P3:3x+6y−3z=6. Then the number of point(s) where plane P1,P2andP3 intersect is/areA0Bexactly oneCexactly twoDinfinite
If P(A∩B)=12 and P(A'∩B')=13,P(A)=2p and P(B)=p , then the value of 9p is ____
View SolutionLet P1:2x+y−z=3 and P2:x+2y+z=2 be two planes. Then, which of the following statement(s) is (are) TRUE? The line of intersection of P1 and P2 has direction ratios 1, 2, −1 (b) The line 3x−49=1−3y9=z3 is perpendicular to the line of intersection of P1 and P2 (c) The acute angle between P1 and P2 is 60o (d) If P3 is the plane passing through the point (4, 2, −2) and perpendicular to the line of intersection of P1 and P2 , then the distance of the point (2, 1, 1) from the plane P3 is 2√3
View SolutionA cubic polynomial P is such that
P(1)=1,P(2)=2,P(3)=3andP(4)=5. ThenP(6) is
View SolutionA point P is 3units away from line L1=3x+4y+5=0and4 units away from the line L2=8x−by+9=0, The reflection of P on L1, is P1 the reflection of P1 on L2, is P2 the reflection of P3, on L2, is P4, Then the area (in sq. units) of figure formed by joining P1P2P3,andP4, is-
View Solution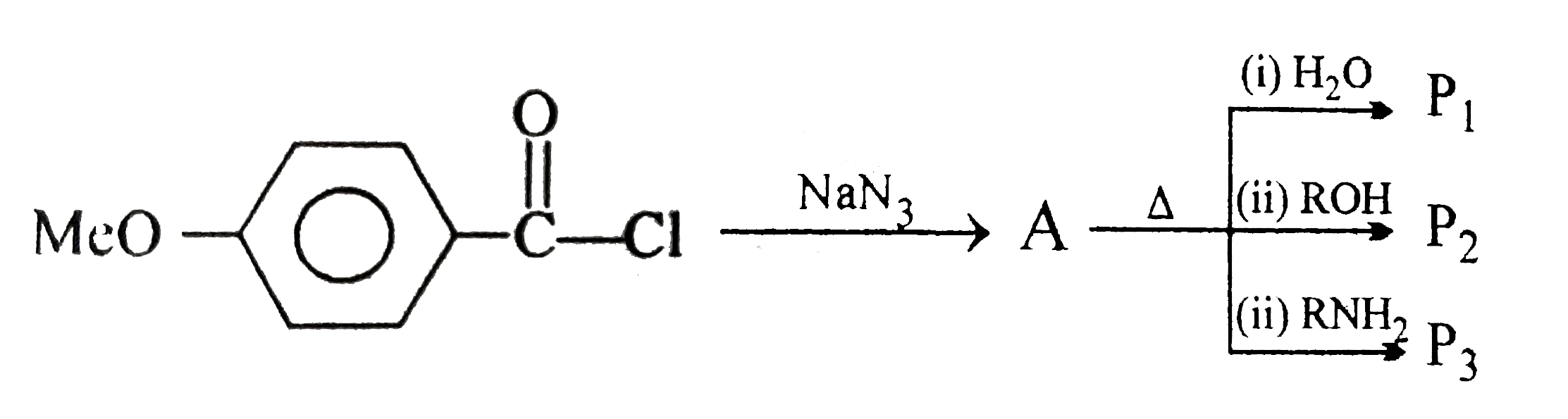
P1,P2,P3,are:
View Solution
