माना f(x)=x−x2+1 है।
कथन - I g(x)=max{f(t):0≤t≤x} है, तो ∫10g(x)dx=2924 होगा।
क्योकि
कथन - II : f(x),(0,12) में वर्धमान तथा (12,1) ओसमान है।
कथन - I सत्य है, कथन - II सत्य है, कथन - II, कथन - I का सही स्पष्टीकरण है।
कथन - I सत्य है, कथन - II सत्य है, कथन - II, कथन - I का सही स्पष्टीकरण नहीं है।
कथन - I सत्य है,परन्तु कथन - II असत्य है
कथन - I असत्य है,परन्तु कथन - II सत्य है
The correct Answer is:A
Step by step video, text & image solution for माना f (x) = x - x^(2) + 1 है। कथन - I g (x) = max {f (t) : 0 le t le x} है, तो int _(0) ^(1) g (x) dx = (29)/(24) होगा। क्योकि कथन - II : f (x), (0, (1)/( 2)) में वर्धमान तथा ((1)/(2), 1) ओसमान है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DEFINITE INTEGRATIONBOOK - ALLEN HINDICHAPTER - DEFINITE INTEGRATIONEXERCISE - Exercise - 03 (गद्यांश आधारित प्रश्न) गद्यांश 1
3 Videos
- DEFINITE INTEGRATIONBOOK - ALLEN HINDICHAPTER - DEFINITE INTEGRATIONEXERCISE - Exercise - 03 (गद्यांश आधारित प्रश्न) गद्यांश 2
3 Videos
- DEFINITE INTEGRATIONBOOK - ALLEN HINDICHAPTER - DEFINITE INTEGRATIONEXERCISE - Exercise - 03 (स्तम्भ सुमेलन)
3 Videos
- CONTINUITY BOOK - ALLEN HINDICHAPTER - CONTINUITY EXERCISE - EXERCISE -05 [B] (JEE-ADVANCED: PREVIOUS YEAR QUESTIONS)
2 Videos
- DETERMINANTBOOK - ALLEN HINDICHAPTER - DETERMINANTEXERCISE - DO YOURSELF -9
1 Videos
Similar Questions
माना g(x)=∫x0f(t)dt, जहाँ f एक फलन है जिसका आरेख दर्शाया गया है।
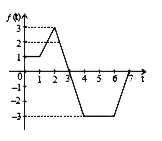
x∈[0,7] में g (x) का अधिकतम मान होगा -
View Solutionफलन f (x) का अन्तराल [ a, b] में, औसत मान संख्या μ=1b−a∫baf(x)dx है |
{1b−a∫ba[f(x)]2dx}1/2 को [a, b] में f का वर्ग माध्य मूल मान कहते है। μ औसत मान प्राप्त करेगा यदि f, [ a, b] का संतत् हो।
अन्तराल [0,π] पर y = sin x की औसत कोटि है -
View Solutionनिम्न प्रश्न में दो स्तम्भ में वत्क्व्य (statements) दिये गए है जिनका सम्मेलन (match) करना है । स्तम्भ - I(Column-I) के वत्क्व्यो को A, B, C तथा D नामित किया गया है जबकि स्तम्भ -II - (Column-II) के वत्क्व्यो को p,q, r तथा s नामित किया ज्ञात है। स्तम्भ- I (Column-I ) में दिए गए कोई एक वत्क्व्य स्तम्भ -II (Column-II ) के एक वत्क्व्य से सही सुमेल करता है।

View Solutionफलन f(x)=⎧⎨⎩e1/x−1e1/x+1जबx≠01जबx=0 का x=0 पर सततता का परीक्षण कीजिए।
View Solutionसमीकरण निकाय λx+y+z=0,−x+λy+z=0,−x−y+λz=0 का एक अशून्य हल होगा यदि λ का वास्तविक मान है
View SolutionLet f(x)=f_1(x)-2f_2 (x), where ,where f_1(x)={((min{x^2,|x|},|x|le 1),(max{x^2,|x|},|x| le 1)) and f_2(x)={((min{x^2,|x|},|x| lt 1),({x^2,|x|},|x| le 1)) and let g(x)={ ((min{f(t):-3letlex,-3 le x le 0}),(max{f(t):0 le t le x,0 le x le 3})) for -3 le x le -1 the range of g(x) is
View SolutionLet f(x)=f1(x)−2f2(x), where
where f(x)={min{x2,|x|},|x|≤1max{x2,|x|},|x|>1
and f2(x)={min{x2,|x|},|x|>1max{x2,|x|},|x|≤1
and let g(x)={min{f(t):−3≤t≤x, −3≤x<0}max{f(t):0≤t≤x, 0≤x≤3}
For x∈(−1,0),f(x)+g(x) is
View SolutionLet f(x)=x3−x2+x+1andg(x) be a function defined by g(x)={Max{f(t):0≤t≤x}0≤x≤13−x1≤x≤2 Then, g(x) is
View SolutionLet f(x)=x3−x2+x+1andg(x)={maxf(t),0≤t≤xfor0≤x≤13−x,1<x≤2 Then, g(x) in [0, 2] is
View SolutionLet f(x)=−x3+x2−x+1andg(x)={min(f(t)),0≤t≤xand0≤x≤1x−1,1<x≤2 Then, the value of limx→1g(g(x)), is........ .
View Solutionमाना f(x)=x3−x2+x+1 और g(x)={max{f(t),0≤t≤x}0≤x≤13−x1<x≤2
फलन g(x) की सततता तथा अवकलनीयता अंतराल (0, 2) पर ज्ञात कीजिए |
View Solutionमाना {−1,−2≤x≤0x2−1,0≤x≤2 तथा g(x)=|f(x)|+f(|x|) तो अंतराल (-2, 2), में फलन g
View SolutionLet f(x)=f1(x)−2f2(x), where ,where f1(x)={(min{x2,|x|}|x|≤1max{x2,|x|}|x|≤1) and f2(x)={(min{x2,|x|}|x|<1{x2,|x|}|x|≤1) and let g(x)={(min{f(t):−3≤t≤x,−3≤x≤0}max{f(t):0≤t≤x,0≤x≤3}) for −3≤x≤−1 the range of g(x) is
View SolutionIf g(x) = int_(0)^(x) f(t)dt whereas 1/2 le f(t) 1 , t in [0,1] And 0 le f(t) le 1/2 , t in (1,2] For then
View SolutionLet f(x)=x3−x2+x+1 g(x) = max I {f(t),0≤t≤x},0≤x≤1=3−x,1<x≤2
Then in [0, 2] the points where g(x) is not differentiable is………
View Solution
