A,B,C are three points
AB=√75,BC=√108
AC=√363.
Check whether these points are on a line or not.Solution in Malayalam
Step by step video & image solution for A,B,C are three points AB=sqrt75,BC=sqrt108 AC=sqrt363. Check whether these points are on a line or not. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Sum of two numbers is 25. The difference is 10. Find the numbers.
View SolutionIn the picture, the square on the hypotenuse of the top most right triangle Is drawn. Calculate the area and the length of a side of the square.
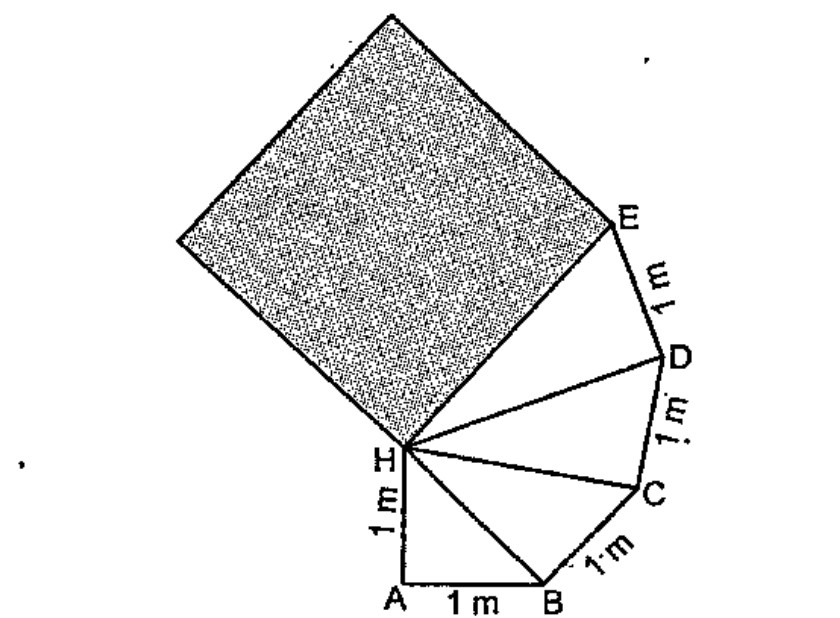 .
.
View SolutionThe value of |[a,a+d,a+2d] , [a+d,a+2d,a+3d] , [a+2d,a+3d,a+4d]|+|[b
View SolutionIf A,B and C are three points on a line and B lies between A and C (as shown in the given figure), then prove that AB+ BC= AC
View Solutionयदि A,B और C तीन बिंदु एक रेखा पर है तथा B,A और C के मध्ये स्थित है तो सिद्ध कीजिएः कि AB+BC=AC.
View Solutionprove that sqrt108 -sqrt75=sqrt3
View Solutionयदि A, B और C एक रेखा पर स्थित तीन बिंदु हैं और B बिंदुओं A और C के बीच में स्थित है ( देखिए आकृति 5.7 ), तो सिद्ध कीजिए कि AB + BC = AC है |

View SolutionIf A, B and C are three points on a line and B is between A and C then prove that AC - BC = AB.
View Solution1) Fragmentation () a) Planaria br 2) Unripe fruits () b) Yeast br 3) Desire () c) Spirogyra br 4) Reproduction () d) Watermelon br
View SolutionIf A,B,C are three points on a line and B lies between A and C, then prove that AC-AB = BC
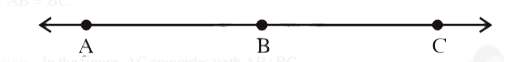
View SolutionIf A,B,C are three points on a line and B lies between A and C, then prove that AC-AB = BC

View SolutionIf A, B and C are three points on a line, and B lies between A and C (see figure), then prove that AB + BC = AC.

View SolutionIf A, B and C are three points on a line, and B lies between A and C (see figure), then prove that AB + BC = AC.

View SolutionA,B,C are three points such that AB=√75,BC=√108,AC=√363.Do they lie on a straight line?
View SolutionA,B,C are three points
AB=√75,BC=√108
AC=√363.
Write these lengths as the product of √3 and as integer.
View Solution
