किसी वक्र सतह पर अपवर्तन के लिए सिद्ध करें कि μ2v−μ1u=μ2−μ1r जहाँ पदों के सामान्य अर्थ है।
माना कि MN एक वक्र सतह है जिसकी वक्रता त्रिज्या R है तथा ये सतह दो माध्यमों को अलग करती है। जिसका अपवर्तनांक क्रमशः μ1 तथा μ2(μ2>μ1)

माना कि i आपतन कोण है तथा OA आपति किरण है। अपवर्तन की घटना के बाद वस्तु O का प्रतिबिम्ब I पर बनता है। r अपवर्तित कोण है।
इसलिए ∠OAN=i,∠IAC=r
माना ∠AOP=α,∠ACP=θ और ∠AIP=β सभी कोणे बहुत छोटी हैं।
∴ समकोण त्रिभुज OPA में tanα=PA−u (∴OP=−u)
समकोण ΔAPC में tanθ=θ=APR
समकोण ΔAPI में tanβ=β=APV
ΔOAC में α+θ=i
θ=i−α ......(i)
ΔIAC
θ=r+β .........(ii)
समीकरण (i) और (ii) से
i−α=r+β,i−r=α+β
स्नेल के नियम से, μ2μ1=ir (∴sinisinr=ir)
μ2μ1r−r=β+α
r(μ1+μ1)=μ1β+μ1α
r का मान समीकरण (ii) से देने पर
(θ−β)(μ2−μ1)=μ1β+μ1α
θ(μ2−μ1)−βμ2+βμ1=μ1β+μ1α
θ(μ2=μ1)=βμ2+μ2α
θ,α तथा β का मान देने पर
(μ2−μ1)APR=μ2APv+μ1AP−u
μ2−μ1R=μ2v−μ1u.μ2v−μ1u=μ2−μ1R
Topper's Solved these Questions
Similar Questions
गॉस के प्रमेय की सहायता से कूलॉम का नियम प्राप्त करें।
11:23View Solutionलगातार बदलनेवाले संकेत को ____ संकेत कहा जाता हैI
02:18View SolutionConsider the situation as shown in the figure. If mu_(1) is the friction coefficient between block A and incline and mu_(2) is the friction coefficient between block B and incline. Find the acceleration of block A if (a) mu_(1) = (1)/(5) , mu_(2) =(2)/(5) and (b) mu_(1) = (2)/(5) , mu_(2) = (1)/(5) .
01:52View SolutionThe observer 'O' sees the distance AB as infinitely large. If refractive index of liquid is mu_(1) and that of glass is mu_(2) , then (mu_(1))/(mu_(2)) is : .
10:55View Solution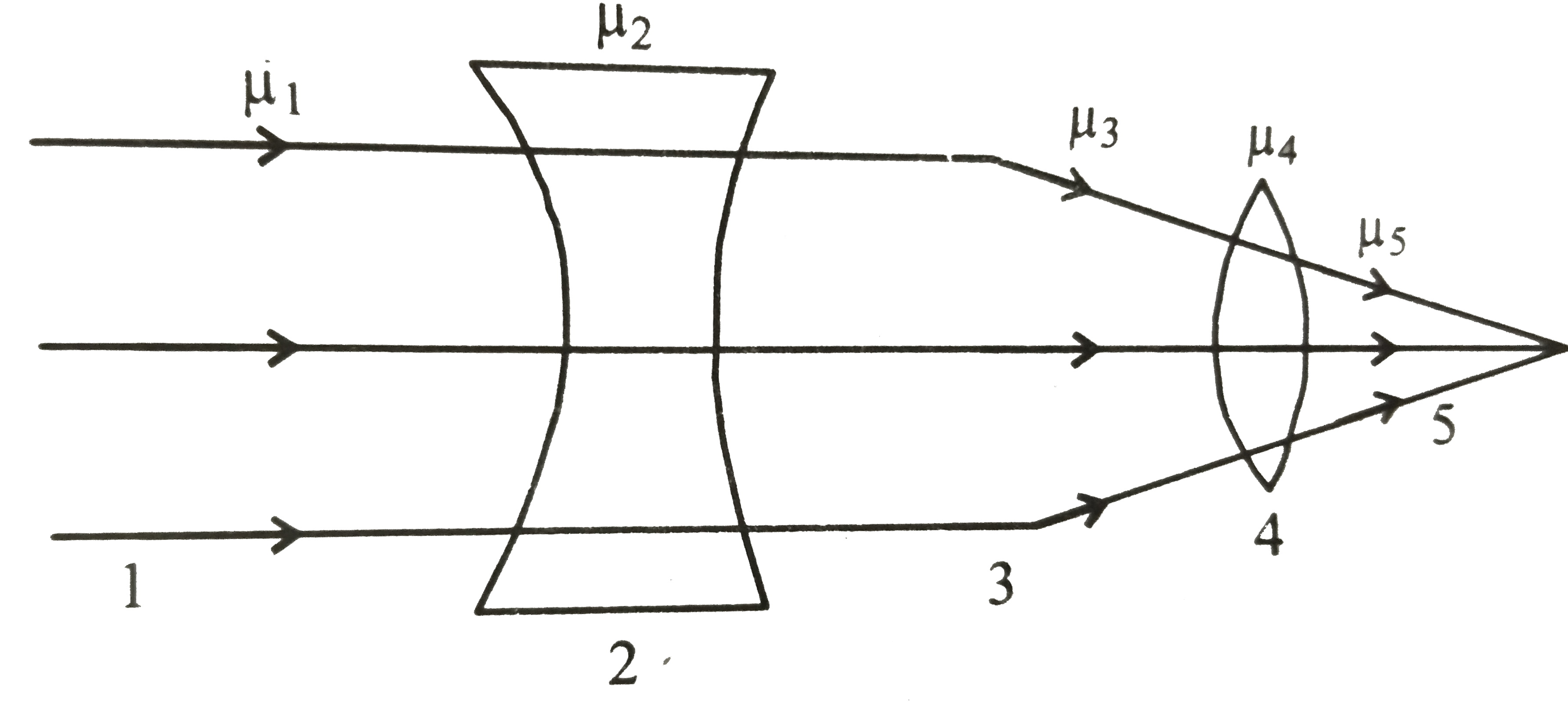
In the figure shown μ1,μ2,μ3,μ4andμ5 are the refractive
indices of the mediums 1,2,3,4 and 5 respectively. Consider
the following:
(1) μ1=μ2 (2) μ3=μ4=μ5
(3) μ2<μ3 (4) μ4>μ5
Which of the above are correct?04:06View Solutionकिसी गोलीय सतह से अपवर्तन के लिए सूत्र μ2v−μ1u=μ2−μ1r निकालें।
02:26View Solutionसदिशों μ1=(1,2,3),μ2=(2,3,1),μ3=(1,3,2) और μ4=(4,6,2) के विषम में निम्नलिखित कथनो पर विचार कीजिये।
I.μ1,μ4 के समान्तर है II. μ2,μ4 के समान्तर है III.μ2,μ3 के समान्तर है
उपरोक्त कथनो में से कोण-सा/से कथन सही है/है?01:38View SolutionThe correct expression for refraction at single convex spherical surface separating two media of refractiv eindices mu_(1) and mu_(2) ( mu_(2) gt mu_(1)) and radius of curvature R is ( u and v are object, image distane respectively )
06:01View SolutionThe reciprocalof ((mu_(2)-mu_(1))/(R)) gives the value of
02:54View Solutionसिद्ध कीजिए कि 1μ2=12μ1.
04:31View SolutionThe refractive indices of a medium for two light waves are μ1andμ2. If μ1>μ2, then which wave will move faster in the medium?
11:54View SolutionThe refractive indices of three media 1,2 and 3 and mu_(1),mu_(2) and mu_(3) respectively (mu_(1) gt mu_(2) gt mu_(3)) . Which of the following statements are correct?
03:51View Solutionसम्बन्ध μ1v−μ2u=μ1−μ2R निकालें जब अवतल गोलीय पृष्ठ से अपेक्षाकृत सघन से अपेक्षाकृत विरल माध्यम (μ2>μ1) में अपवर्तन हो और बनने वाला प्रतिबिम्ब, वास्तविक हो | चिन्ह परिपाटी और अपनाई गई अभिधारणाएँ बताएँ |
01:38View SolutionThe correct expression for refraction at single convex spherical surface separating two media of refractive indices μ1andμ2(μ2>μ1) and radius of curvature R is ( u and v are object, image distane respectively )
06:08View SolutionThe reciprocalof (μ2−μ1R) gives the value of
02:46View SolutionObtain an expression for refraction at a single convex spherical surface separating the two media having refractive indices mu_(1) (rarer medium) and mu_(2) (denser medium) i.e., a relation between u, v, mu_(1),mu_(2) and R.
View Solution
