The correct expression for refraction at single convex spherical surface separating two media of refractiv eindices μ1andμ2(μ2>μ1) and radius of curvature R is ( u and v are object, image distane respectively )
μ1u−μ2v=(μ1−μ2)R
μ1v−μ2u=(μ1−μ2)R
μ2u−μ1v=(μ2−μ1)R
μ2v−μ1u=(μ2−μ1)R
The correct Answer is:D
Step by step video, text & image solution for The correct expression for refraction at single convex spherical surface separating two media of refractiv eindices mu_(1) and mu_(2) ( mu_(2) gt mu_(1)) and radius of curvature R is ( u and v are object, image distane respectively ) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RAY OPTICSBook:TARGET PUBLICATIONChapter:RAY OPTICSExercise:CRITICALTHINKING
Explore 34 Videos
- RAY OPTICSBook:TARGET PUBLICATIONChapter:RAY OPTICSExercise:COMPETITIVE THINKING
Explore 60 Videos
- MEASUREMENTSBook:TARGET PUBLICATIONChapter:MEASUREMENTSExercise:EVALUATION TEST
Explore 17 Videos
- REFRACTION OF LIGHT Book:TARGET PUBLICATIONChapter:REFRACTION OF LIGHT Exercise:EVALUATION TEST
Explore 12 Videos
Similar Questions
A spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?
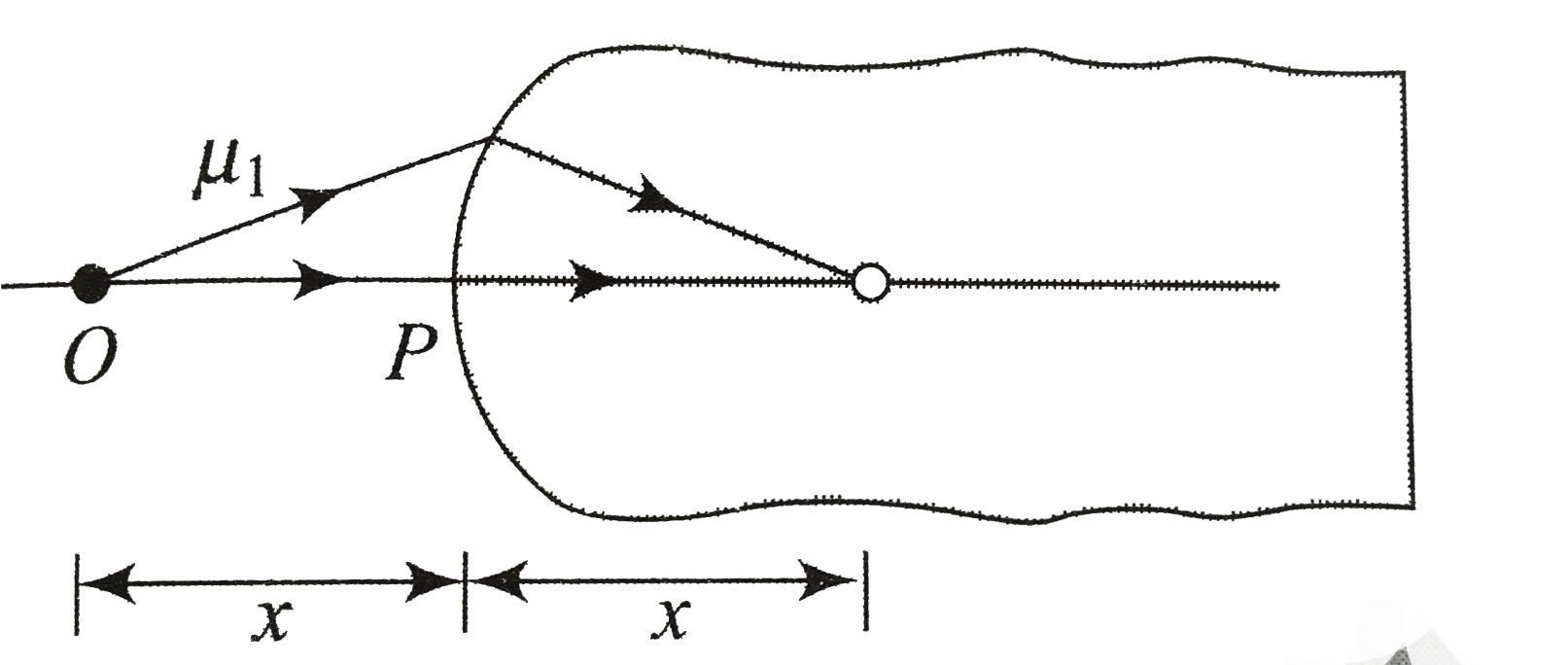
View SolutionWhat is the relation between the refractive indicesμ,μ1 and μ2 if the behaviour of light rays is shown in Figure.
View Solution
Knowledge Check
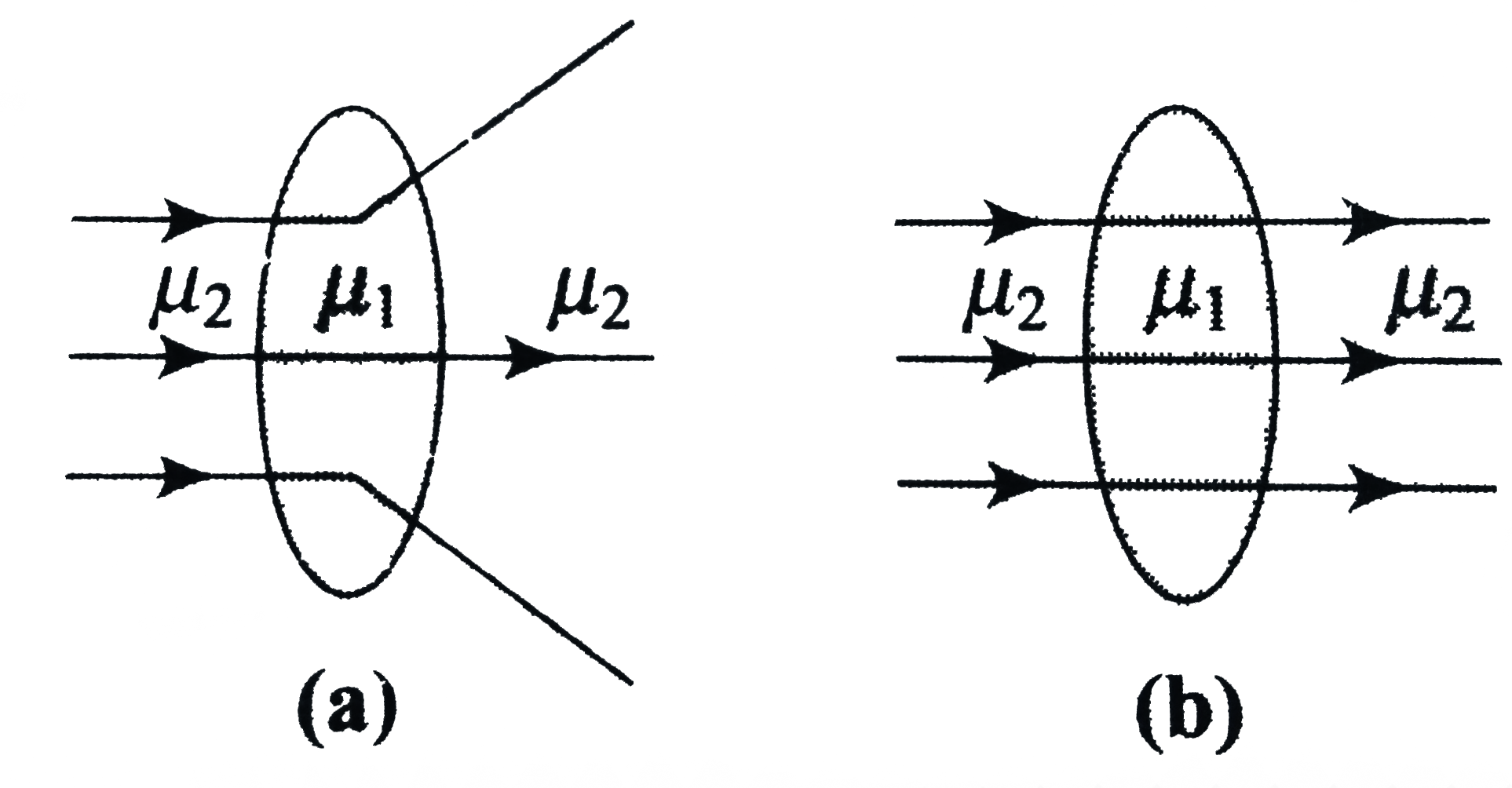
If the behaviour of light rays is as shown in the figure. The relation between refractive indices μ,μ1 "and" μ2 is
 Aμ>μ2>μ1Bμ<μ2<μ1Cμ<μ2,μ=μ1Dμ2<μ1,μ=μ2
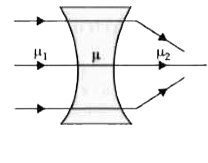
Aμ>μ2>μ1Bμ<μ2<μ1Cμ<μ2,μ=μ1Dμ2<μ1,μ=μ2Two optical media of refractive indices μ1 and μ2 contain x and y waves of same colour in the same thickness. Their refractive indices ratio is equal to
A(x−y)xB(x+y)xCxy−xDyxTwo optical media of refractive indices μ1 and μ2 contain x and y waves of same colour in the same thickness. Their refractive indices ratio is equal to
Ax−yxB(x+Y)xCxy−xDyx
A monochromatic light is incident on the plane interface AB between two media of refractive indices μ1 and (μ2>μ1) at an angle of incidence θ as shown in Fig.
The angle θ is infinitesimally greater than the critical angle for the two media so that total internal reflection takes place. Now, if a transparent slab DEFG of uniform thickness and of refractive index μ3 is introduced on the interface (as shown in the figure), show that for any value of μ3 all light will ultimately be reflected back into medium II.

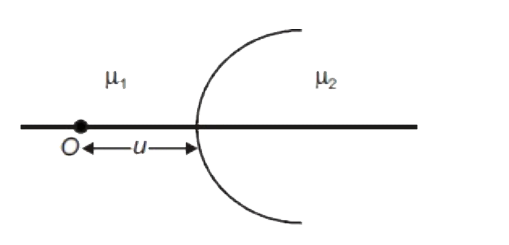
View SolutionThe diagram shows a spherical surface which separates two media of refractive index, μ1andμ2. Respectively. Now, a point object is placed on the principal axis as shown in the figure. Then
View SolutionThe length of the optical path of two media in contact of length d1 and d2 of refractive indices μ1 and μ2 respectively, is
View SolutionThe length of the optical path of two media in contact of length d1 and d2 of refractive indices μ1 and μ2 respectively, is
View SolutionA thin plano-convex lens fits exactly into a thin plano-concave lens. Their plane surfaces are parallel to each other. The lenses are made of different material of refractive indices μ1 and μ2 and R is the radius of curvature of the curved surfaces of the lenses, if rays are incident parallel to principal axis on lens of refractive index.
View Solution

