ABC is a right angled triangle with AB = 4, BC = 3, AC = 5. P is mid point of AB. Q is a point on AC such that ⌊PQA=90∘. Then BA.
43√13
54√13
34√12
None
The correct Answer is:a
Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBook:AAKASH SERIESChapter:PROPERTIES OF TRIANGLESExercise:LECTURE SHEET EXERCISE - IV (More than one correct answer Type Questions)
Explore 3 Videos
- PROPERTIES OF TRIANGLESBook:AAKASH SERIESChapter:PROPERTIES OF TRIANGLESExercise:LECTURE SHEET EXERCISE - IV (Matrix Matching Type Questions)
Explore 2 Videos
- PROPERTIES OF TRIANGLESBook:AAKASH SERIESChapter:PROPERTIES OF TRIANGLESExercise:LECTURE SHEET EXERCISE - III (Straight Objective Type Question)
Explore 62 Videos
- PLANESBook:AAKASH SERIESChapter:PLANESExercise:ADVANCED SUBJECTIVE TYPE QUESTIONS
Explore 30 Videos
- PROPERTIES OF VECTORSBook:AAKASH SERIESChapter:PROPERTIES OF VECTORSExercise:PRACTICE EXERCISES
Explore 55 Videos
Similar Questions
ABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
View SolutionABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:
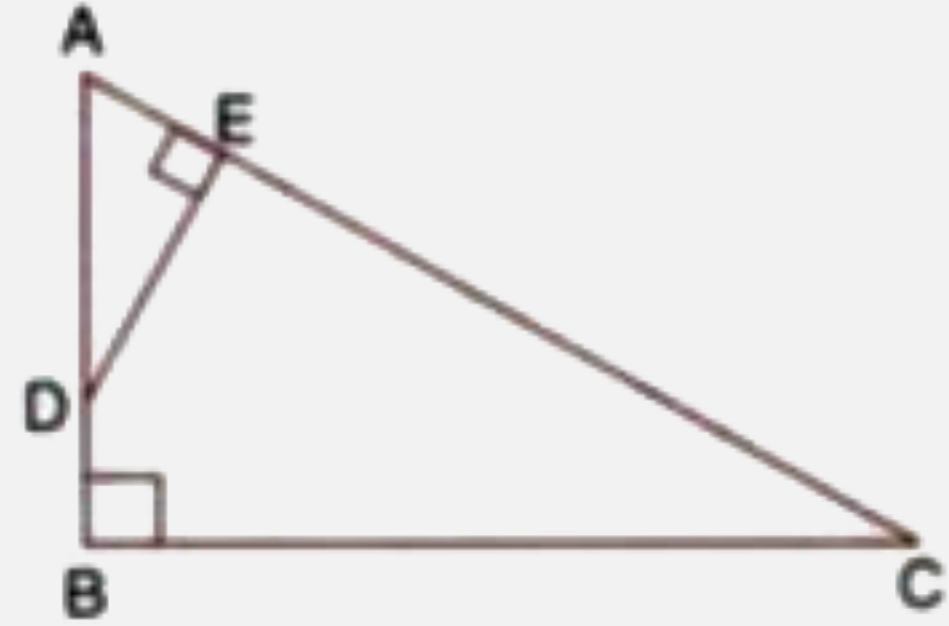
ΔADE~ΔACB.
View Solution
Knowledge Check
ABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :
 A1 cmB1.25 cmC1.5 cmDnone of these
A1 cmB1.25 cmC1.5 cmDnone of theseABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :
A1 cmB1.25 cmC1.5 cmD2 cmIf ABC is a right angled triangle at B and M, N are the mid-points of AB and BC, then 4(AN2+CM2) is equal to :
A4AC2B6AC2C5AC2D54AC2
ABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :

View SolutionIn a right-angled triangle ABC,∠ABC=90∘ and D is mid-point of AC. Prove that BD=12AC.
View SolutionIn a right-angled triangle ABC, if angle B=90°, BC = 3 cm and AC = 5 cm, then the length of side AB is
View SolutionABC is a right angled triangle with ∠ABC=90∘, D is any point on AB and DE is perpendicular to AC.
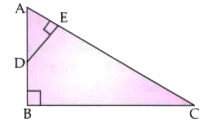
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
View SolutionABC is a right triangle with ∠B=90∘ and AC - AB = 1. If BC=√n then AB is
View Solution

