कथन-I : यदि 2a + 3b + 6c = 14, जहाँ a, b व c∈R हो, तो a2+b2+c2 का न्यूनतम मान 4 होगा। क्योंकि
कथन-II : समतल px+qy+rz=1 की मूल बिन्दु से लम्बवत् दूरी 1√p2+q2+r2 होगी।
कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण है।
कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण नहीं है।
कथन-I सत्य है परन्तु कथन-II असत्य है।
कथन-I असत्य है परन्तु कथन-II सत्य है।
The correct Answer is:A
Step by step video, text & image solution for कथन-I : यदि 2a + 3b + 6c = 14, जहाँ a, b व c in R हो, तो a^(2) + b^(2) + c^(2) का न्यूनतम मान 4 होगा। क्योंकि कथन-II : समतल px + qy + rz = 1 की मूल बिन्दु से लम्बवत् दूरी 1/sqrt(p^(2) + q^(2) + r^(2)) होगी। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- 3D-COORDINATE GEOMETRY BOOK - ALLEN HINDICHAPTER - 3D-COORDINATE GEOMETRY EXERCISE - EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) गद्यांश आधारित प्रश्न (Comprehension Based Questions) गद्यांश # 1:
3 Videos
- 3D-COORDINATE GEOMETRY BOOK - ALLEN HINDICHAPTER - 3D-COORDINATE GEOMETRY EXERCISE - EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) गद्यांश आधारित प्रश्न (Comprehension Based Questions) गद्यांश # 2:
3 Videos
- 3D-COORDINATE GEOMETRY BOOK - ALLEN HINDICHAPTER - 3D-COORDINATE GEOMETRY EXERCISE - EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) स्तम्भ सुमेलन (Match the column)
3 Videos
- AREA UNDER THE CURVEBOOK - ALLEN HINDICHAPTER - AREA UNDER THE CURVEEXERCISE - Exercise-05 [B]
21 Videos
Similar Questions
चार बिन्दु A(2, 1, 0), B(1, 0, 1), C(3, 0, 1) तथा D(0, 0, 2) दिए गए हैं। बिन्दु D, रेखा L पर स्थित है, जो बिन्दु A,B तथा C से बने समतल के लम्बकोणीय हैं। उपरोक्त जानकारी के आधार पर, निम्न प्रश्नों के उत्तर दीजिए :
समतल ABC का समीकरण है:
View Solutionयदि कोई रेखा P(x1,y1,z1) से गुजरती है तथा जिसके दिक् अनुपात a, b, c हों, तो रेखा का समीकरण x−x1a=y−y1b=z−z1c होगा तथा इसके लम्बवत् एवं P से गुजरने वाले समलत का समीकरण a(x−x1)+b(y−y1)+c(z−z1)=0 होगा और दो समतलों a1x+b1y+c1z+d1=0 तथा a2x+b2y+c2z+d2=0 के प्रतिच्छेद से गुजरने वाले समतल की समीकरण (a1x+b1y+c1z+d1)+k(a2x+b2y+c2z+d2)=0 होगी।
उपरोक्त जानकारी के आधार पर, निम्न प्रश्नों के उत्तर दीजिए:
बिन्दु (1, -2, 3) की समतल x-y+z= 5 से, रेखा x2=y3=z−3−4 के समान्तर मापी गई दूरी होगी -
View Solutionनिम्न प्रश्नों में दो स्तम्भ में क्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है। स्तम्भ-I (Column-I) के वक्तव्यों कोA, B,C तथाD नामित किया गया है जबकिस्तम्भ-II (Column-II) के वक्तव्यों को, q, r तथा 5 नामित किया गया है। स्तम्भ-I(Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Columm-II) के एक वक्तव्य से सही सुमेल करता है।
निम्न समतल युग्म को उनकी प्रतिच्छेदी रेखाओं से सुमेलित कीजिए।
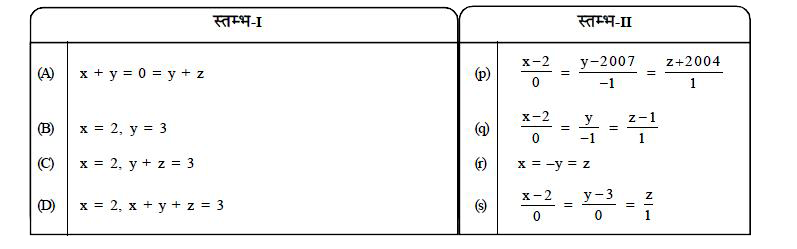
View Solutionवक्र f(x)=x2+bx−b के बिन्दु (1,1) पर स्पर्श रेखा तथा निर्देशी अक्षो से बना त्रिभुज प्रथम चतुर्थांश में स्थित है | यदि इसका क्षेत्रफल 2 है, तो b का मान है -
View Solutionस्तम्भ(A)स्तम्भ(B)(1) बिन्दु (3,4) की मूल बिन्दु से दुरी होगी (a)37(2)यदि बिन्दु (3,5) ,(6,9) तथा (x,3) संरेख हो, तो का x मान होगा: (b)3(3)बिंदुओं (3,5) तथा (-4,2) को मिलाने वाली रेखा की प्रवणता होगी :(b)72(4)kके किस मान के लिए रेखाएँ y=x+1,y=2+3 तथा संगामी होंगी?(c)5(5)रेखा की x+sqrt(3)y+7=0 मुलबिन्दु से लाम्बिक दुरी होगी (d)4
View Solutionरेखायें l1 व l2 प्रतिच्छेदी है तो उनके बीच की न्यूनतम दूरी होगी -
View Solutionयदि O मूल बिन्दु तथा A(a,b,c) है तो A से जाने वाले एवं OA लम्ब समतल का समीकरण है -
View Solutionमाना p,q∈R, यदि 2−√3 द्विघाती समीकरण x2+px+q=0 का एक मूल है, तो
View Solutionयदि समीकरण x2+2mx+m2−2m+6=0 के मूल बराबर हो, तो m का मान होगा।
View Solutionयदि समीकरण ix2−2(i+1)x+(2−i)=0 का एक मूल 2-i हो तो समीकरण का दूसरा मूल होगा।
View Solutionजहाँ ∣∣α2−β2∣∣=74 जहाँ α,β समीकरण 2x2+7x+c=0 के मूल हो, तो c का मान है।
View Solutionयदि बिन्दु (x+1,2),(1,x+2),(1x+1,2x+1) समरेखीय हो तो x का मान है
View Solutionयदि m1 व m2 अतिपरवलय x225−y216=1 की स्पर्श रेखाओं की प्रवणताएं हो, जो बिन्दु (6,2) से गुजरती है , तो
View Solutionयदि समीकरण x2+x+1=0 के मूल a,b हैं तथा x2+px+q=0 के मूल हैं, ab,ba तो p+q का मान है
View Solutionयदि 1x3−2x2−x+2=Ax−1+Bx+1+Cx−2 हो, तो A+B+C का मान ज्ञात कीजिए।
View Solution
