कथन-I : यदि एक समतल, बिन्दु kA(→a) रखता है तथा सदिश b तथा c: के समान्तर है, तो इसकी सदिश समीकरण →r=→a+λ→b+μ→c होगी, जहाँ λ व μ प्राचल हैं तथा →b/→c है। क्योंकि
कथन-II : यदि तीन सदिश समतलीय हैं, तो कोई एक को अन्य दो के रेखीय संयोजन के रूप में लिखा जा सकता है।
कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण है।
कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण नहीं है।
कथन-I सत्य है परन्तु कथन-II असत्य है।
कथन-I असत्य है परन्तु कथन-II सत्य है।
The correct Answer is:C
Step by step video, text & image solution for कथन-I : यदि एक समतल, बिन्दु kA(veca) रखता है तथा सदिश b तथा c: के समान्तर है, तो इसकी सदिश समीकरण vecr = veca + lambda vecb + mu vecc होगी, जहाँ lambda व mu प्राचल हैं तथा vecb//vecc है। क्योंकि कथन-II : यदि तीन सदिश समतलीय हैं, तो कोई एक को अन्य दो के रेखीय संयोजन के रूप में लिखा जा सकता है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- 3D-COORDINATE GEOMETRY BOOK - ALLEN HINDICHAPTER - 3D-COORDINATE GEOMETRY EXERCISE - EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) गद्यांश आधारित प्रश्न (Comprehension Based Questions) गद्यांश # 1:
3 Videos
- 3D-COORDINATE GEOMETRY BOOK - ALLEN HINDICHAPTER - 3D-COORDINATE GEOMETRY EXERCISE - EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) गद्यांश आधारित प्रश्न (Comprehension Based Questions) गद्यांश # 2:
3 Videos
- 3D-COORDINATE GEOMETRY BOOK - ALLEN HINDICHAPTER - 3D-COORDINATE GEOMETRY EXERCISE - EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) स्तम्भ सुमेलन (Match the column)
3 Videos
- AREA UNDER THE CURVEBOOK - ALLEN HINDICHAPTER - AREA UNDER THE CURVEEXERCISE - Exercise-05 [B]
21 Videos
Similar Questions
चार बिन्दु A(2, 1, 0), B(1, 0, 1), C(3, 0, 1) तथा D(0, 0, 2) दिए गए हैं। बिन्दु D, रेखा L पर स्थित है, जो बिन्दु A,B तथा C से बने समतल के लम्बकोणीय हैं। उपरोक्त जानकारी के आधार पर, निम्न प्रश्नों के उत्तर दीजिए :
समतल ABC का समीकरण है:
View Solutionयदि कोई रेखा P(x1,y1,z1) से गुजरती है तथा जिसके दिक् अनुपात a, b, c हों, तो रेखा का समीकरण x−x1a=y−y1b=z−z1c होगा तथा इसके लम्बवत् एवं P से गुजरने वाले समलत का समीकरण a(x−x1)+b(y−y1)+c(z−z1)=0 होगा और दो समतलों a1x+b1y+c1z+d1=0 तथा a2x+b2y+c2z+d2=0 के प्रतिच्छेद से गुजरने वाले समतल की समीकरण (a1x+b1y+c1z+d1)+k(a2x+b2y+c2z+d2)=0 होगी।
उपरोक्त जानकारी के आधार पर, निम्न प्रश्नों के उत्तर दीजिए:
बिन्दु (1, -2, 3) की समतल x-y+z= 5 से, रेखा x2=y3=z−3−4 के समान्तर मापी गई दूरी होगी -
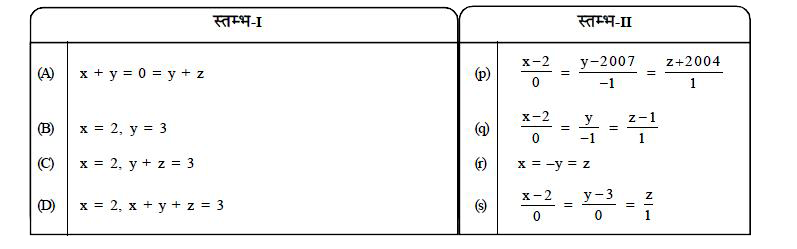
View Solutionनिम्न प्रश्नों में दो स्तम्भ में क्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है। स्तम्भ-I (Column-I) के वक्तव्यों कोA, B,C तथाD नामित किया गया है जबकिस्तम्भ-II (Column-II) के वक्तव्यों को, q, r तथा 5 नामित किया गया है। स्तम्भ-I(Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Columm-II) के एक वक्तव्य से सही सुमेल करता है।
निम्न समतल युग्म को उनकी प्रतिच्छेदी रेखाओं से सुमेलित कीजिए।
View Solutionवक्र f(x)=x2+bx−b के बिन्दु (1,1) पर स्पर्श रेखा तथा निर्देशी अक्षो से बना त्रिभुज प्रथम चतुर्थांश में स्थित है | यदि इसका क्षेत्रफल 2 है, तो b का मान है -
View Solutionयदि →a,→b,→c तीन असमतलीय एकांक सदिश है तथा →a×(→c×→b)=→b+→c√2 तो →a और →b के मध्य कोण है -
View Solutionयदि →a.→b=0 तथा →a+→b,→b के साथ 60° का कोण बनाते हैं तो |→a| बराबर है
View Solutionमाना कि △PQR एक त्रिभुज है तथा →a=−−→QR,→b=−−→RP तथा →c=−−→PQ है | यदि |→a|=12,∣∣→b∣∣=4√3 तथा →b.→c=24 तो निम्न में से कोण-सा (से) सही है
View Solutionयदि [→a×→b→b×→c→c×→a]=λ[→a→b→c]2 तो λ बराबर है |
View Solutionयदि बिंदु A जिसका स्थिति सदिश ¯a+2¯b है तथा सदिश ¯a,AB को 2:3 के अनुपात में विभाजित करता है तो B का स्थिति सदिश है:
View Solutionमाना ¯a,¯b,¯c तीन शून्येतर सदिश है जिनमें कोई भी दो संरेखीय नहीं हैं | यदि सदिश ¯a+2¯b तथा ¯c एक रेखीय हों, तो ¯a+2¯b+6¯c=
View Solution→a,→b,→c क्रमश 3,4,5 परिमाण के सदिश है। यदि प्रत्येक सदिश अन्य दो सदिशो के योग पर लम्ब हो, तो सदिश →a+→b+→c का परिमाण ज्ञात किजिए।
View Solutionयदि →a,→b,→c समान परिमाण के परस्पर लम्ब सदिश हो तो सिद्ध कीजिए कि सदिश →a+→b+→c सदिशों →a,→b और →c के साथ बराबर कोण बनाता है।
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solutionयदि →a,→b,→c इस प्रकार कि इकाई सदिश है कि →a.→b=0=→a.→c तथा →b और →c के मध्य का कोण π6 है , तब सिद्ध कीजिए कि →a=±2(→b×→c)
View Solutionयदि →a,→b तथा →c समबाहु त्रिभुज के शीर्ष के स्थिति सदिश हो जिसका लम्ब केंद्र मूलबिंदु है , तो →a+→b+→c का मान ज्ञात कीजिए।
View Solutionसदिशों (→a−→b) और (→c−→b) दोनों के लंबवत एक मात्रक सदिश ज्ञात कीजिए जहाँ →a=ˆi+2ˆj+ˆk,→b=2ˆi+ˆj तथा →c=3ˆi−4ˆj−ˆk.
View Solution
