An idal coil of 10 is connected in series with a resitance of 5Ω and a battery of 5V. After 2s, after the connection is made, the current flowing ( in ampere) in the circuit is
(1-e)
e
e−1
(1−e−1)
The correct Answer is:D
To solve the problem, we need to find the current flowing in the circuit after 2 seconds. We will use the formula for the current in an LR circuit, which is given by:
I(t)=I0(1−e−tτ)
where:
- I(t) is the current at time t,
- I0 is the maximum current (steady-state current),
- e is the base of the natural logarithm,
- τ is the time constant of the circuit.
1. Identify the given values:
- Inductance L=10H
- Resistance R=5Ω
- Voltage E=5V
- Time t=2s
2. Calculate the maximum current I0:
The maximum current I0 can be calculated using Ohm's law:
I0=ER=5V5Ω=1A
3. Calculate the time constant τ:
The time constant τ is given by:
τ=LR=10H5Ω=2s
4. Substitute the values into the current equation:
Now we can substitute I0, t, and τ into the current equation:
I(t)=I0(1−e−tτ)=1(1−e−22)=1(1−e−1)
5. Calculate e−1:
The value of e−1 is approximately 0.3679:
I(t)=1(1−0.3679)≈1×0.6321≈0.6321A
Final Answer:
The current flowing in the circuit after 2 seconds is approximately 0.6321A.
- I(t) is the current at time t,
- I0 is the maximum current (steady-state current),
- e is the base of the natural logarithm,
- τ is the time constant of the circuit.
- Inductance L=10H
- Resistance R=5Ω
- Voltage E=5V
- Time t=2s
The maximum current I0 can be calculated using Ohm's law:
I0=ER=5V5Ω=1A
The time constant τ is given by:
τ=LR=10H5Ω=2s
Now we can substitute I0, t, and τ into the current equation:
I(t)=I0(1−e−tτ)=1(1−e−22)=1(1−e−1)
The value of e−1 is approximately 0.3679:
I(t)=1(1−0.3679)≈1×0.6321≈0.6321A
The current flowing in the circuit after 2 seconds is approximately 0.6321A.
Topper's Solved these Questions
- SOLVED PAPERS 2018BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - Assertion and Reasons
10 Videos
- SOLVED PAPERS 2018BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - JIPMER
22 Videos
- SOLVED PAPERS 2018BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - JIPMER
22 Videos
- SOLVED PAPER 2017BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPER 2017EXERCISE - Solved papers 2017(JIPMER)
32 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced E. Integer Type Questions
13 Videos
Similar Questions
An ideal coil of 10 henry is joined in series with a resistance of 5 ohm and a battery of 5 volt. 2 second after joining, the current flowing in ampere in the circuit will be
View SolutionA coil of 40H inductance is connected in series with a resistance of 8 ohm and the combination is joined to the terminals of a 2V battery. The time constant of the circuit
View SolutionFind the voltage drop across a capacitor connected with a resistance and a battery of 60 V in series after a long time.
View SolutionAn inductor of 10mH is connected to a 18V battery through a resistor of 10kΩ and a switch After a long time, when the maximum current is set up in the circuit, the current is switched off. Calculate the cur- rent in the circuit after 2 μs.
View SolutionAn inductor of inducance 5.0 H, having a negligible resistance, is connected in series with a 100Ω resistor and a battery of emf 2.0 V. Find the potential difference across the resistor 20 ms after the circuit is switched on.
View SolutionAn inductor of 10mH is connected to a 18V battery through a resistor of 10kΩ and a switch. After a long time, when the maximum current is set up in the circuit, the battery is disconnected from the circuit. Calculate the current in the circuit after 15μs
View SolutionA 6 V, 12 W lamp is connected in series with a resistor R and a source of voltage 12 V.
What is the current flowing through the circuit?
View SolutionFor resistances are connected by an ideal battery of emf 15 V, the circuit is in steady - state then the current (in ampere) in wire AB is :
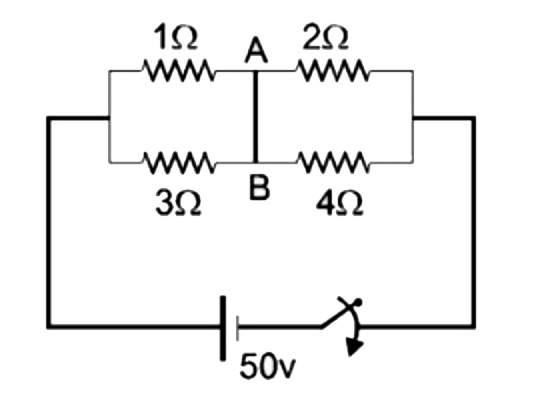
View SolutionTwo cells having emf's of 10 V and 8 V, respectively, are connected in series with a resistance of 24Ω In the external circuit. Their internal resistances are 2Ω/V (proportional to their emf's). Find the current in the circuit

View Solutionn identical cells each of emf 6 V , connected in series with an external resistor of 5Ω, carry a current of 10A. If two cells are connected wrongly in series with the same external resistor, the current flowing through the cells will be 8A. Find the value of n and r the internal resistance of each cell.
View Solution