In a YDSE green light of wavelength 500 nm is used. Where will be the second bright fringe be formed for a set up in which separation between slits is 4 mm and the screen is placed 1 m from the slits?
To solve the problem of finding the position of the second bright fringe in a Young's Double Slit Experiment (YDSE) using green light, we can follow these steps:
Step 1: Identify the given values
- Wavelength of light, λ=500nm=500×10−9m
- Distance between the slits, d=4mm=4×10−3m
- Distance from the slits to the screen, D=1m
Step 2: Use the formula for the position of bright fringes
The position of the n-th bright fringe in a YDSE is given by the formula:
yn=nλDd
where:
- yn is the position of the n-th bright fringe,
- n is the order of the fringe (for the second bright fringe, n=2),
- λ is the wavelength,
- D is the distance from the slits to the screen,
- d is the separation between the slits.
Step 3: Substitute the values into the formula
For the second bright fringe (n=2):
y2=2×(500×10−9m)×(1m)4×10−3m
Step 4: Calculate the position
Calculating y2:
y2=2×500×10−9×14×10−3=1000×10−94×10−3=10004×10−6=250×10−6m
Converting this to millimeters:
y2=250×10−6m=0.25mm
Step 5: Final Answer
The position of the second bright fringe is:
0.25mm
- Wavelength of light, λ=500nm=500×10−9m
- Distance between the slits, d=4mm=4×10−3m
- Distance from the slits to the screen, D=1m
The position of the n-th bright fringe in a YDSE is given by the formula:
yn=nλDd
where:
- yn is the position of the n-th bright fringe,
- n is the order of the fringe (for the second bright fringe, n=2),
- λ is the wavelength,
- D is the distance from the slits to the screen,
- d is the separation between the slits.
For the second bright fringe (n=2):
y2=2×(500×10−9m)×(1m)4×10−3m
Calculating y2:
y2=2×500×10−9×14×10−3=1000×10−94×10−3=10004×10−6=250×10−6m
Converting this to millimeters:
y2=250×10−6m=0.25mm
The position of the second bright fringe is:
0.25mm
Topper's Solved these Questions
Similar Questions
A source emitting light of wavelengths 480 nm and 600 nm is used in a double slit interference experiment. The separation between the slits is 0.25 mm and the interference is observed on a screen placed at 150 cm from the slits. Find the linear separation between the first maximum (next to the central maximum) corresponding to the two wavelengths.
View SolutionWhat is the value of angular fringe width if fringe width is = 0.4 nm and separation between slit and screen is 2m.
View Solution
Knowledge Check
A beam of light consisting of two wavelengths 650nm and 520nm is used to obtain interference fringes in a Young's double slit experiment.
(a) Find the distance of the third bright fringe on the screen from the central maximum for the wavelength 650nm.
(b) What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide? The distance between the slits is 2mm and the distance between the plane of the slits and screen is 120cm.A1.17 mmB2.52 mmC1.56 mmD3.14 mmIn double slit experiment using light of wavelength 600nm, the angular width of a fringe formed on a distant screen is 0.1∘. What is the spacing between the two slits ?
A3.44×10−4mB1.54×10−4mC1.54×10−3mD1.44×10−3m
White coheral light (400 nm 700 nm ) is sent through the slit of a Young.s double slit experiment. The separation between the slits is 0.5 mm and the screen is 50 away from the slits . There is a hole in the screen at a point 1.0 mm away (along the width of the fringes) from the central line. Which wavelengths (s) will be absent in the light coming from the hole ?
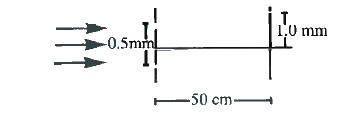
View SolutionIn Young’s double slit experiment, using light of wavelength 600 nm, 10th bright fringe is obtained on a screen, 3mm from the centre of the pattern. If the screen is 120 cm away from the slits, calculate:
(i) Distance between the two slits,
(ii) Fringe width, i.e. fringe separation.
View SolutionIn a Young's double slit experiment , the slits are Kept 2mm apart and the screen is positioned 140cm away from the plane of the slits. The slits are illuminatedd with light of wavelength 600nm. Find the distance of the third brite fringe. From the central maximum . in the interface pattern obtained on the screen frings from the central maximum. 3
View SolutionIn double slit experiment using light of wavelength 600nm, the angular width of a fringe formed on a distant screen is 0.1∘. What is the spacing between the two slits ?
View SolutionA beam of light consisting of two wavelengths, 650 nm and 520 nm is used to obtain interference fringes in Young's double-slit experiment. What is the least distance (in m) from a central maximum where the bright fringes due to both the wavelengths coincide ? The distance between the slits is 3 mm and the distance between the plane of the slits and the screen is 150 cm.
View SolutionWhite light of wavelength in range 400 nm to 700 nm is incident normaly on a young's double slit experiment apparatus. The distance betweenn slits is d=1 mm and distance between plane of the slits and screen in 0.8 m. At a point on the screen just in front of one of the slits the missing wavelength is (are)
View Solution
