A diver at a depth of 12 m in water (μ=4/3) sees the sky in a cone of semi-vertical angle
sin−1(43)
tan−1(43)
sin−1(34)
90∘
The correct Answer is:C
To solve the problem, we need to determine the semi-vertical angle of the cone in which a diver at a depth of 12 meters in water sees the sky. The refractive index of water is given as μ=43.
1. Understanding the Problem:
- The diver is at a depth of 12 meters in water.
- The refractive index of water μwater=43.
- The refractive index of air μair=1.
- We need to find the semi-vertical angle θ of the cone of light that the diver can see.
2. Using Snell's Law:
- According to Snell's law, we have:
μwatersin(θ)=μairsin(r)
- Here, r is the angle of refraction when light exits the water into the air. Since the light emerges at the critical angle, we can consider r=90∘.
3. Substituting Values:
- Substituting the known values into Snell's law:
43sin(θ)=1⋅sin(90∘)
- Since sin(90∘)=1, we can simplify this to:
43sin(θ)=1
4. Solving for sin(θ):
- Rearranging the equation gives:
sin(θ)=34
5. Finding θ:
- Now, we can find θ by taking the inverse sine:
θ=sin−1(34)
6. Conclusion:
- The semi-vertical angle θ of the cone in which the diver sees the sky is sin−1(34).
Final Answer:
θ=sin−1(34)
- The diver is at a depth of 12 meters in water.
- The refractive index of water μwater=43.
- The refractive index of air μair=1.
- We need to find the semi-vertical angle θ of the cone of light that the diver can see.
- According to Snell's law, we have:
μwatersin(θ)=μairsin(r)
- Here, r is the angle of refraction when light exits the water into the air. Since the light emerges at the critical angle, we can consider r=90∘.
- Substituting the known values into Snell's law:
43sin(θ)=1⋅sin(90∘)
- Since sin(90∘)=1, we can simplify this to:
43sin(θ)=1
- Rearranging the equation gives:
sin(θ)=34
- Now, we can find θ by taking the inverse sine:
θ=sin−1(34)
- The semi-vertical angle θ of the cone in which the diver sees the sky is sin−1(34).
θ=sin−1(34)
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - medical entrance special format question
23 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.7
10 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
A water tank has the shape of an inverted right circular cone, whose semi-vertical angle is tan−1(12). Water is poured into it at a constant rate of 5 cu m/min. Then, the rate (in m/min) at which the level of water is rising at the instant when the depth of water in the tank is 10 m is
View SolutionA ship is salling in river. An observe is situated at a depth h in water (μw). If x>>h, find the angle made form vertical, of the line of slight of ship.

View Solution
Knowledge Check
A fish which is at a depth of 12 cm in water (μ=43) is viewed by an observer on the bank of a lake. Its apparent depth as observed by the observer is :
A3 cmB9 cmC12 cmD16 cm
A ring of mass m and radius R rests in equilibrium on a smooth cone of semi-vertical angle 45∘ as shown. The radius of the cone is 2R. the radius of circular cross section of the ring is r(r<<R).
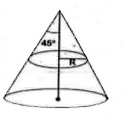
What will be the tension in the ring?
View SolutionWater is dropped at the rate of 2 m3/s into a cone of semi-vertical angle is 45∘ . If the rate at which periphery of water surface changes when the height of the water in the cone is 2m is d. Then the value of 5d is _____ m/sec
View SolutionWater is dropped at the rate of 2 m3/s into a cone of semi-vertical angle is 45∘ . If the rate at which periphery of water surface changes when the height of the water in the cone is 2m is d. Then the value of 5d is _____ m/sec
View SolutionA coin is placed at the bottom of a beaker containing water (refractive index=4/3) at a depth of 12cm. By what height the coin appears to be raised when seen from vertical above ?
View SolutionA bell tent consists of a conical portion above a cylindrical portion near the ground. For a given volume and a circular base of a given radius, the amount of the canvas used is a minimum when the semi-vertical angle of the cone is cos−123 (b) sin−123 cos−113 (d) none of these
View SolutionA chain of mass 'm' and radius 'r' is placed onto a cone of semi vertical angle θ. Cone rotated with angular velocity ω. Find the tension in the chain if it does not slide on the cone.
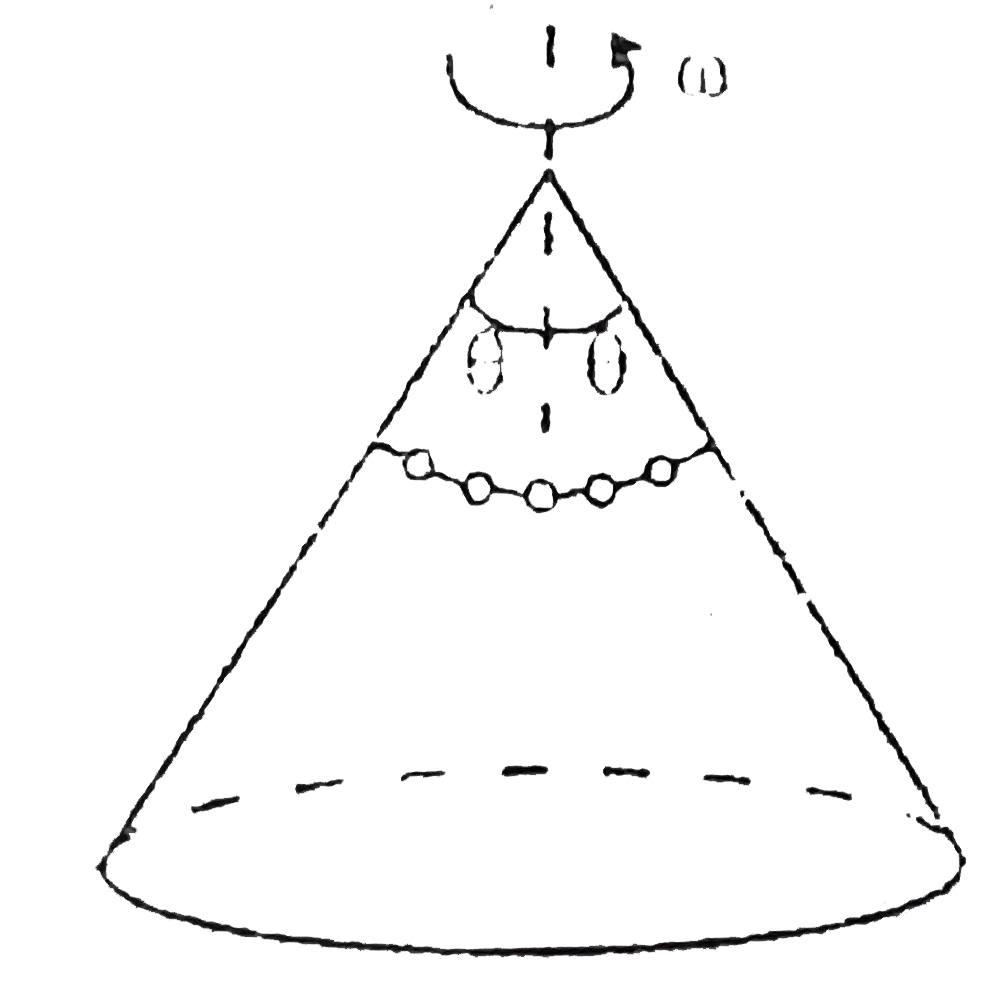
View SolutionThe volume of the greatest cylinder which can be inscribed in a cone of height 30 cm and semi-vertical angle 300 is (a)4000π√3 (b) 4000π3cm3 (c) 4000π√3cm3 (d) none of these
View Solution
