When a lens of refractive index , then the lens looks to be dissapeared only, if
The correct Answer is:C
To determine when a lens of refractive index n1 appears to disappear, we can analyze the situation using the lens maker's formula and the concept of optical power.
1. Understanding the Concept of Disappearance:
- A lens appears to disappear when it does not refract light, which means its optical power is zero.
2. Using the Lens Maker's Formula:
- The lens maker's formula relates the focal length f of a lens to its refractive indices and radii of curvature:
1f=(n1−n2)(1r1−1r2)
- Here, n1 is the refractive index of the lens, and n2 is the refractive index of the surrounding medium.
3. Setting the Power to Zero:
- For the lens to appear to disappear, its power must be zero, which implies:
f→∞(or equivalently, 1f=0)
- Therefore, we set the right-hand side of the lens maker's formula to zero:
(n1−n2)(1r1−1r2)=0
4. Analyzing the Equation:
- The equation can be satisfied if either:
- n1−n2=0 (which means n1=n2)
- or 1r1−1r2=0 (which means r1=r2, indicating a plano-convex or plano-concave lens).
5. Conclusion:
- Since we are interested in the case where the lens disappears due to the refractive index, we focus on the first condition:
n1=n2
- Therefore, the lens will appear to disappear when the refractive index of the lens n1 is equal to the refractive index of the surrounding medium n2.
6. Final Answer:
- The correct option is:
Option 3: n1=n2
- A lens appears to disappear when it does not refract light, which means its optical power is zero.
- The lens maker's formula relates the focal length f of a lens to its refractive indices and radii of curvature:
1f=(n1−n2)(1r1−1r2)
- Here, n1 is the refractive index of the lens, and n2 is the refractive index of the surrounding medium.
- For the lens to appear to disappear, its power must be zero, which implies:
f→∞(or equivalently, 1f=0)
- Therefore, we set the right-hand side of the lens maker's formula to zero:
(n1−n2)(1r1−1r2)=0
- The equation can be satisfied if either:
- n1−n2=0 (which means n1=n2)
- or 1r1−1r2=0 (which means r1=r2, indicating a plano-convex or plano-concave lens).
- Since we are interested in the case where the lens disappears due to the refractive index, we focus on the first condition:
n1=n2
- Therefore, the lens will appear to disappear when the refractive index of the lens n1 is equal to the refractive index of the surrounding medium n2.
- The correct option is:
Option 3: n1=n2
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - medical entrance special format question
23 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.7
10 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
A lens is made of flint glass (refractive index =1.5). When the lens is immersed in a liquid of refractive index 1.25 , the focal length:
View SolutionAn equiconvex lens of refractive index n2 is placed such that the refractive index of the surrouding media is as shown. The lens :
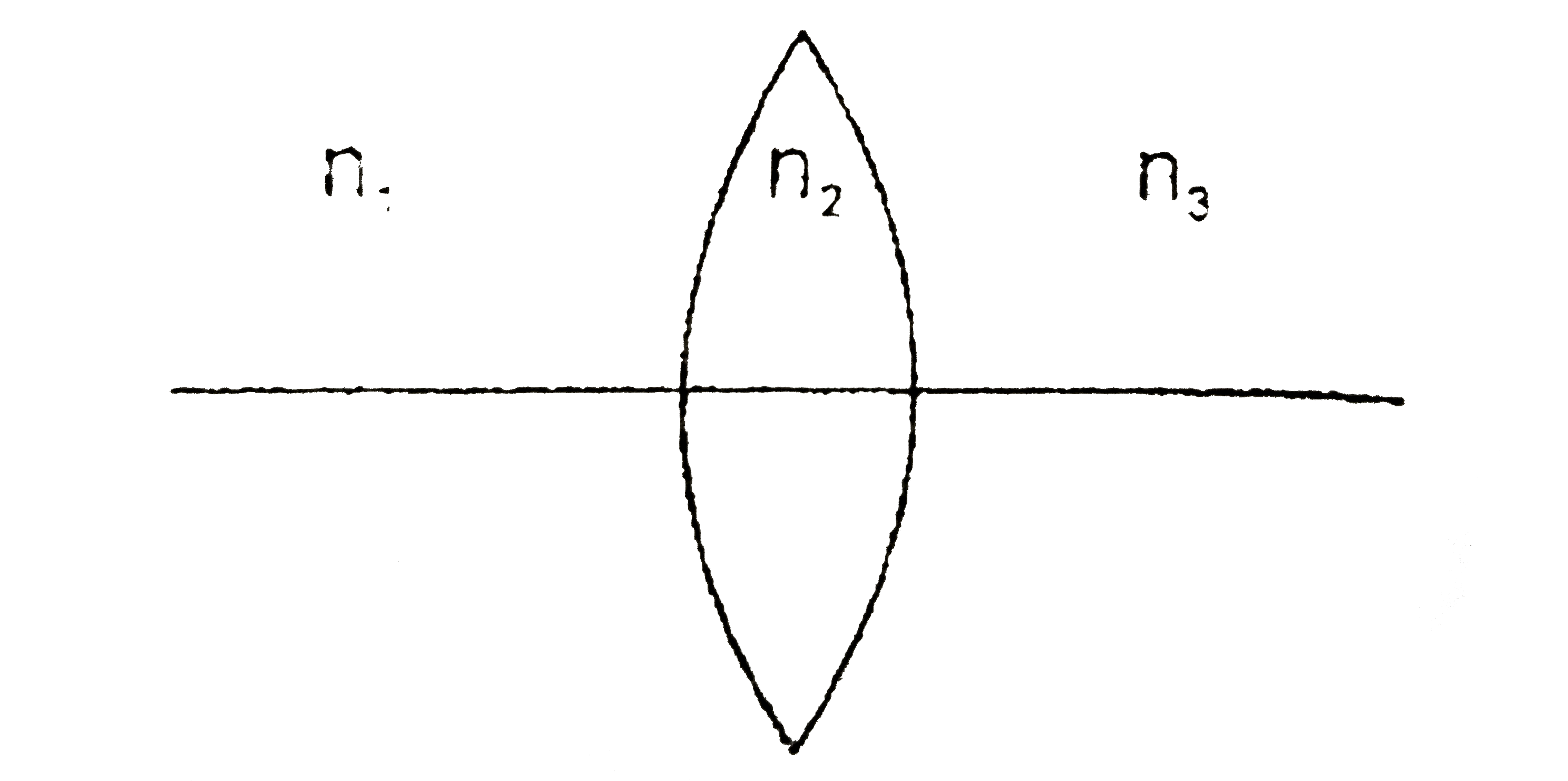
View SolutionFocal length of a convex lens of refractive index 1.5 is 2 cm. Focal length of lens when immersed in a liquid of refractive index 1.25 will be
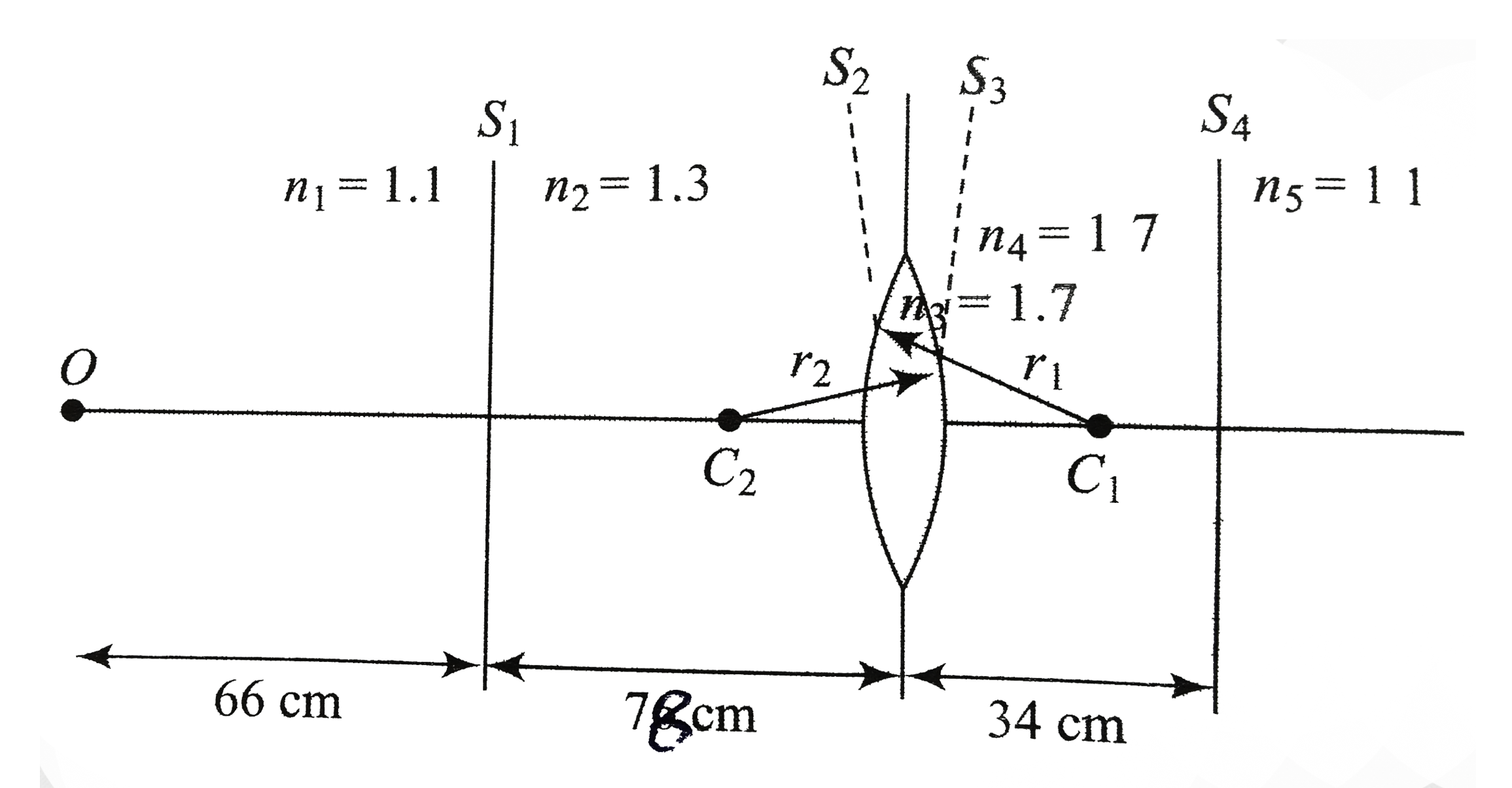
View SolutionA biconvex lens separates two media of refractive indices 1.3 and 1.7. the refractive index of the lens is 1.5 and the radii of curvature of the two sides of the lens are r1=10cm and r2=60cm .
The medium of refractive index 1.3 extends to 78 cm from the lens and that of refractive index 1.7 extends of 34 cm from the lens. A luminous object O is at a distance of 144 cm from the lens. Find the position of the final image from the lens.
View SolutionThe focal length of lens of refractive index 1.5 in air is 30cm When it is immersed in water of refractive index 43 ,then its focal length will be
View SolutionA plano-convex lens is made of refractive index of 1.6. The focal length of the lens is
View SolutionA bi-convex lens is cut from the middle as shown in figure. Refractive index of material of lens is 32. Now lens-1 (as shown in figure) is immersed in a liquid of refractive index μ0. By doing so it is observed that its focal length becomes equal to lens-2. What is the value of μ0 ?

View SolutionA glass lens of refractive index 1.45 when immersed in a transparent liquid becomes invisible. Under what condition does it happen ?
View SolutionA biconcave lens made of a transparent material of refractive index 1.25 is immersed in water of refractive index 1.33. Will the lens behave as a converging or a diverging lens? Give reason.
View SolutionA biconcave lens made of a transparent material of refractive index 1.5 is immersed in water of refractive index 1.33. Will the lens behave as a converging or a diverging lens? Give reason.
View Solution
