An object has image thrice of its original size when kept at and from a convex lens. Focal length of the lens is
less than 8 cm
8 cm
16 cm
between 8 and 16 cm
The correct Answer is:D
To find the focal length of the convex lens given that the image is thrice the size of the object when placed at distances of 8 cm and 16 cm, we can use the lens formula and the magnification formula.
1. Understand the Magnification Formula:
The magnification (M) produced by a lens is given by:
M=VU
where V is the image distance and U is the object distance. Given that the image is thrice the size of the object, we have:
M=3
2. Set Up the Object Distances:
For the two cases, the object distances are:
- Case 1: U1=−8cm (negative because the object is on the same side as the incoming light)
- Case 2: U2=−16cm
3. Apply the Magnification Formula for Both Cases:
For Case 1:
3=V1−8
Rearranging gives:
V1=−24cm
For Case 2:
3=V2−16
Rearranging gives:
V2=−48cm
4. Use the Lens Formula:
The lens formula is given by:
1F=1V−1U
We will apply this for both cases.
For Case 1:
1F=1−24−1−8
Simplifying:
1F=−124+324=224=112
Therefore, F=12cm.
For Case 2:
1F=1−48−1−16
Simplifying:
1F=−148+348=248=124
Therefore, F=12cm.
5. Conclusion:
The focal length of the convex lens is:
F=12cm
The magnification (M) produced by a lens is given by:
M=VU
where V is the image distance and U is the object distance. Given that the image is thrice the size of the object, we have:
M=3
For the two cases, the object distances are:
- Case 1: U1=−8cm (negative because the object is on the same side as the incoming light)
- Case 2: U2=−16cm
For Case 1:
3=V1−8
Rearranging gives:
V1=−24cm
3=V2−16
Rearranging gives:
V2=−48cm
The lens formula is given by:
1F=1V−1U
We will apply this for both cases.
1F=1−24−1−8
Simplifying:
1F=−124+324=224=112
Therefore, F=12cm.
1F=1−48−1−16
Simplifying:
1F=−148+348=248=124
Therefore, F=12cm.
The focal length of the convex lens is:
F=12cm
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - medical entrance special format question
23 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.7
10 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
A pin of length 2.0 cm lies along the principal axis of a converging lens, the centre being at a distance of 11 cm from the lens. The focal length of the lens is 6 cm. Find the size of the image.
View SolutionGraph of position of image vs position of point object from a convex lens is shown. Then, focal length of the lens is
_E01_287_Q01.png)
View SolutionAn object is placed in front of two convex lenses one by one at a distance u from the lens. The focal lengths of the lenses are 30 cm and 15 cm respectively. If the size of image formed in the two cases is same, then u is
View SolutionA point object is placed at a distance of 12cm from a convex lens of focal length 10cm. On the other side of the lens, a convex mirror is placed at a distance of 10cm from the lens such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
nature of the image
View SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cm
View SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cm
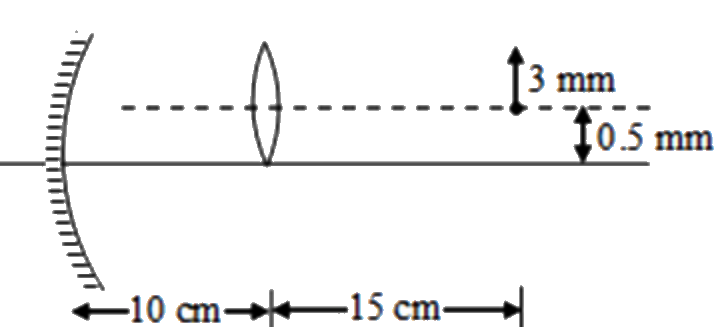
View SolutionA concave mirror of focal length 20 cm and a convex lens of focal length 10 cm are kept with their optic axes parallel but separated by 0.5 mm as shown in the figure. The distance between the the lens and mirror in 10 cm. An object of height 3 mm is placedon the optic axis of lens at a distnace between the lens and mirror is 10 cm. An object of height 3 mm is placed on the optic axis of lens at a distance 15 cm from the lens. Find the length of the image formed the mirror in mm.
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View SolutionWhen an object is placed 40cm from a diverging lens, its virtual image is formed 20cm from the lens. The focal length and power of lens are
View Solution
