An AC voltage source of variable angular frequency (ω) and fixed amplitude V0 is connected in series with a capacitance C and an electric bulb of resistance R (inductance zero). When (ω) is increased
The bulb glows dimmer
The bulb glows brighter
Total impedance of the circuit is unchanged
Total impedance of the circuit increases
The correct Answer is:B
To solve the problem, we need to analyze the behavior of the circuit as the angular frequency (ω) is increased. The circuit consists of a capacitor C and a resistor R in series with an AC voltage source of fixed amplitude V0.
1. Understanding Impedance in the Circuit:
The total impedance Z of a series circuit with a resistor and a capacitor is given by the formula:
Z=√R2+(1ωC)2
Here, R is the resistance, C is the capacitance, and ω is the angular frequency.
Hint: Remember that impedance combines resistance and reactance (due to capacitance) in a right triangle.
2. Effect of Increasing ω:
As ω increases, the term 1ωC decreases. This means that the capacitive reactance XC=1ωC decreases. Therefore, the total impedance Z will also decrease because:
Z = \sqrt{R^2 + X_C^2} \quad \text{(where X_C = \frac{1}{\omega C})}
Hint: Consider how changes in frequency affect capacitive reactance.
3. Calculating RMS Current:
The RMS current Irms in the circuit can be calculated using Ohm's law for AC circuits:
Irms=VrmsZ
Since Vrms=V0√2 for a fixed amplitude V0, we can express it as:
Irms=V0/√2Z
As Z decreases (due to increasing ω), Irms will increase.
Hint: Remember that a decrease in impedance leads to an increase in current.
4. Effect on the Bulb:
The brightness of the bulb is directly related to the power dissipated in the resistor, which can be expressed as:
P=I2rmsR
Since Irms increases as ω increases, the power P will also increase, causing the bulb to glow brighter.
Hint: Consider how power is related to current and resistance.
5. Conclusion:
Therefore, when the angular frequency (ω) is increased, the bulb will glow brighter.
Final Answer:
The correct option is: The bulb glows brighter.
The total impedance Z of a series circuit with a resistor and a capacitor is given by the formula:
Z=√R2+(1ωC)2
Here, R is the resistance, C is the capacitance, and ω is the angular frequency.
As ω increases, the term 1ωC decreases. This means that the capacitive reactance XC=1ωC decreases. Therefore, the total impedance Z will also decrease because:
Z = \sqrt{R^2 + X_C^2} \quad \text{(where X_C = \frac{1}{\omega C})}
The RMS current Irms in the circuit can be calculated using Ohm's law for AC circuits:
Irms=VrmsZ
Since Vrms=V0√2 for a fixed amplitude V0, we can express it as:
Irms=V0/√2Z
As Z decreases (due to increasing ω), Irms will increase.
The brightness of the bulb is directly related to the power dissipated in the resistor, which can be expressed as:
P=I2rmsR
Since Irms increases as ω increases, the power P will also increase, causing the bulb to glow brighter.
Therefore, when the angular frequency (ω) is increased, the bulb will glow brighter.
The correct option is: The bulb glows brighter.
Similar Questions
An alternating voltage, of angular frequency ω is induced in electric circuit consistin of inductance L and capacitance C, connected in parallel. Then across the inductance coil
View SolutionThe power factor of an AC circuit having resistance (R) and inductance (L) connected in series and an angular velocity ω is
View SolutionFor an LCR series circuit with an ac source of angular frequency ω.
View SolutionA box P and a coil Q are connected in series with an ac source of variable frequency. The emf of the source is constant at 10 V. Box P contains a capacitance 1μf and a resistance of 32Ω. Coil Q has a self inductance of 4.9 mH and a resistance of 68Ω in series. The frequency is adjusted so that maximum current flows in P and Q.
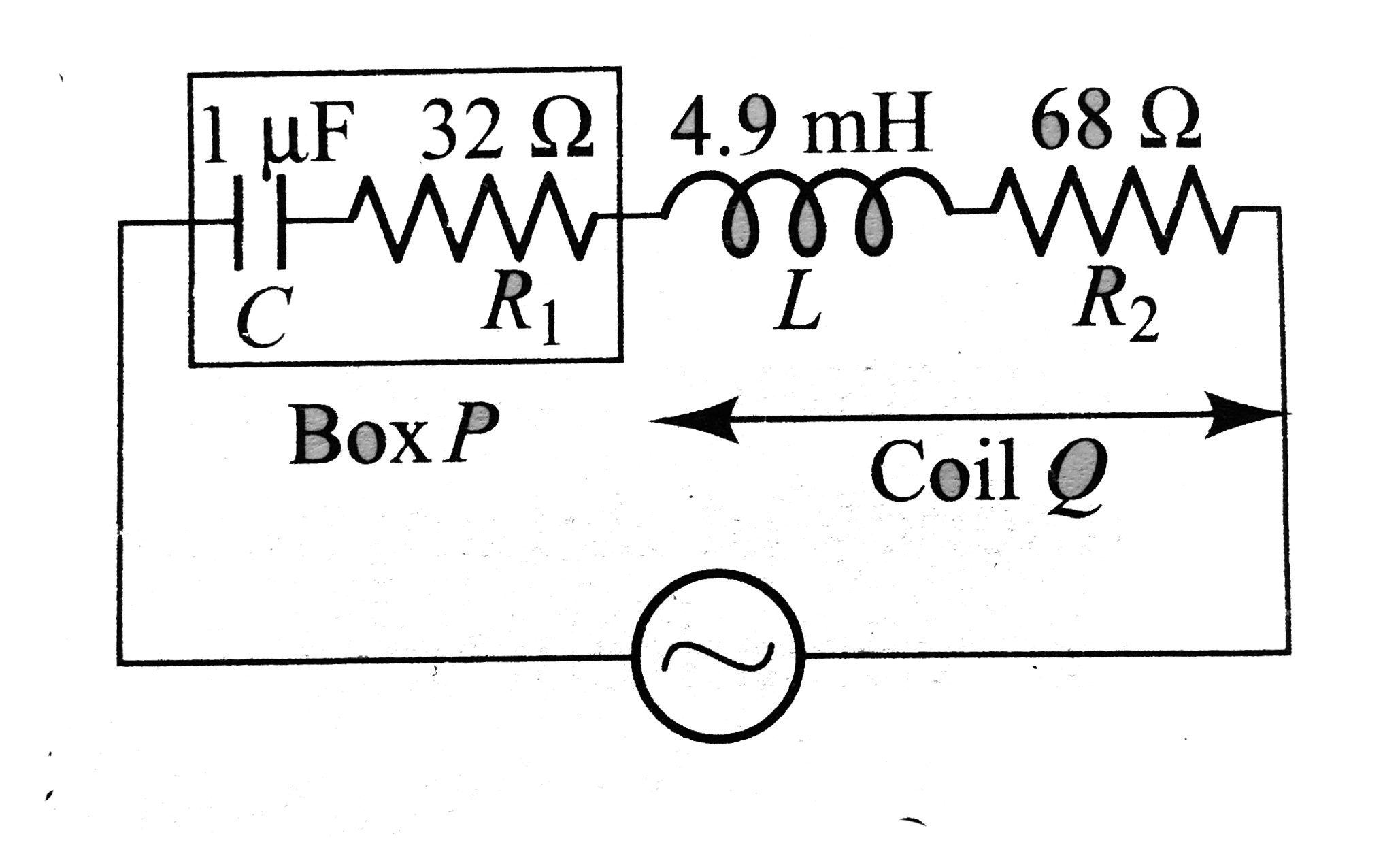
The voltage across P is
View SolutionA coil of self-inductance L is connected in series with a bulb B and an AC source. Brightness of the bulb decreases when
View SolutionA box P and a coil Q are connected in series with an AC source of variable frequency.The EMF of source is constant at 10V.Box P contains a capacitance of 1μF in series with a resistance of 32Ω.Coil Q has a self inductance 4.9mH and a resistance of 68Ω.The frequency is adjusted so that the maximum current flows in P and Q.Find the impedance of P and Q at this frequency.Also find the voltage across P and Q respectively.
View SolutionThree bulbs of 40W,60Wand100W are connected in series with a 240V source.
View SolutionA 6 V, 12 W lamp is connected in series with a resistor R and a source of voltage 12 V.
What is the purpose of the resistor R?
View SolutionAn AC voltage source is applied across an R-C circuit. Angular frequency of the source is ω, resistance is R and capacitance is C. The current registered is I. If now the frequency of source is changed to ω2 (but maintaining the same voltage), the current in the circuit is found to be two third. calculate the ratio of reactance to resistance at the original frequency ω .
View SolutionThe current in a circuit containing a capacitance C and a resistance R in series leads over the applied voltage of frequency ω2π by.
View Solution
