In a circuit containing R and L , as the frequency of the impressed AC increase, the impedance of the circuit
decreases
increases
remains unchanged
first increases and then decreases
The correct Answer is:B
To solve the question regarding the impedance of a circuit containing a resistor (R) and an inductor (L) as the frequency of the impressed AC increases, we can follow these steps:
1. Understanding Impedance:
The impedance (Z) of an R-L circuit is given by the formula:
Z=√R2+X2L
where XL is the inductive reactance.
2. Inductive Reactance:
The inductive reactance XL is defined as:
XL=ωL=2πfL
where f is the frequency of the AC source and L is the inductance.
3. Substituting Inductive Reactance:
By substituting XL into the impedance formula, we get:
Z=√R2+(2πfL)2
4. Analyzing the Effect of Frequency:
As the frequency f increases, the term 2πfL also increases. Therefore, the expression for impedance becomes:
Z=√R2+(2πfL)2
This indicates that as f increases, the value of (2πfL)2 increases, leading to an increase in the overall impedance Z.
5. Conclusion:
Since the impedance Z increases with an increase in frequency f, we can conclude that the impedance of the circuit increases as the frequency of the impressed AC increases.
Final Answer:
The impedance of the circuit increases as the frequency of the impressed AC increases.
The impedance (Z) of an R-L circuit is given by the formula:
Z=√R2+X2L
where XL is the inductive reactance.
The inductive reactance XL is defined as:
XL=ωL=2πfL
where f is the frequency of the AC source and L is the inductance.
By substituting XL into the impedance formula, we get:
Z=√R2+(2πfL)2
As the frequency f increases, the term 2πfL also increases. Therefore, the expression for impedance becomes:
Z=√R2+(2πfL)2
This indicates that as f increases, the value of (2πfL)2 increases, leading to an increase in the overall impedance Z.
Since the impedance Z increases with an increase in frequency f, we can conclude that the impedance of the circuit increases as the frequency of the impressed AC increases.
The impedance of the circuit increases as the frequency of the impressed AC increases.
Similar Questions
As the frequency of an alternating current increases, the impedance of the circuit
View SolutionWhen the frequency of AC is doubled, the impedance of an LCR series circuit
View SolutionAn AC of frequency f is flowing in a circuit containing a resistance R and capacitance C in series. The impedance of the circuit is equal to
View SolutionIn an AC circuit containing only capacitance the current
View SolutionIn the circuit shown in the figure, find:
(a) the reactance of the circuit
(b) impedance of the circuit
(c )the current
(d) readings of the ideal AC voltmeters(these are hot wire instruments and read rms values)
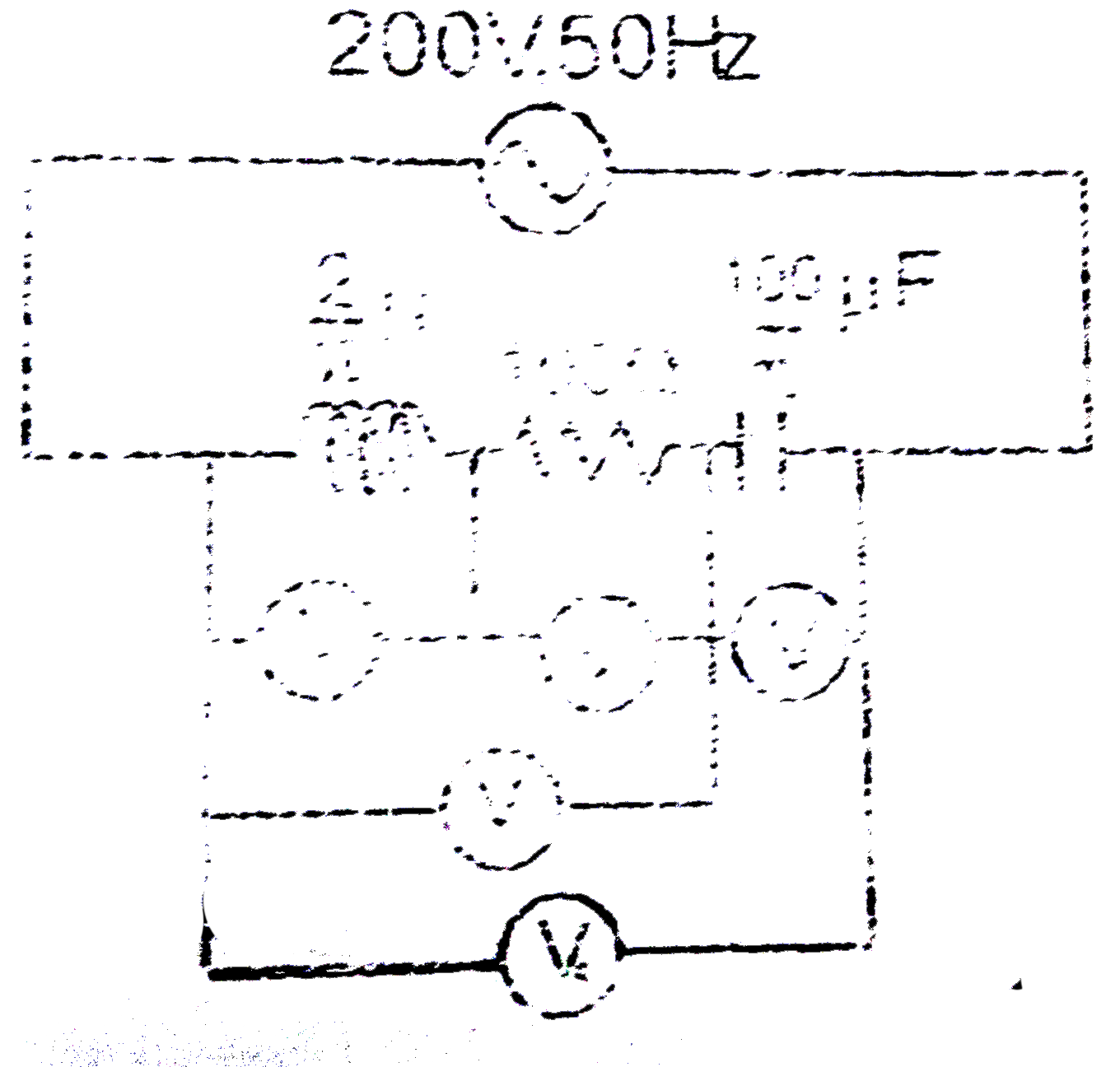
View SolutionAssertion: In L-C-R series AC circut, XL=XC=R at a given frequency. When frequency is doubled, the impedance of the circuit is √132 R.
Reason: The given frequency is resonance frequency.
View SolutionWhich increase in frequency of an AC supply , the impedance of an L-C-R series circuit
View SolutionSame current is flowing in two alternating circuits. The first circuit contains only inductances and the other contains only a capacitor, if the frequency of the e.m.f of AC is increased, the effect on the value of the current will be
View SolutionSame current is flowing in two alternating circuits. The first circuit contains only inductances and the other contains only a capacitor, if the frequency of the e.m.f of AC is increased, the effect on the value of the current will be
View SolutionIf frequency of R- L circuit is f then impedence will be
View Solution