Question

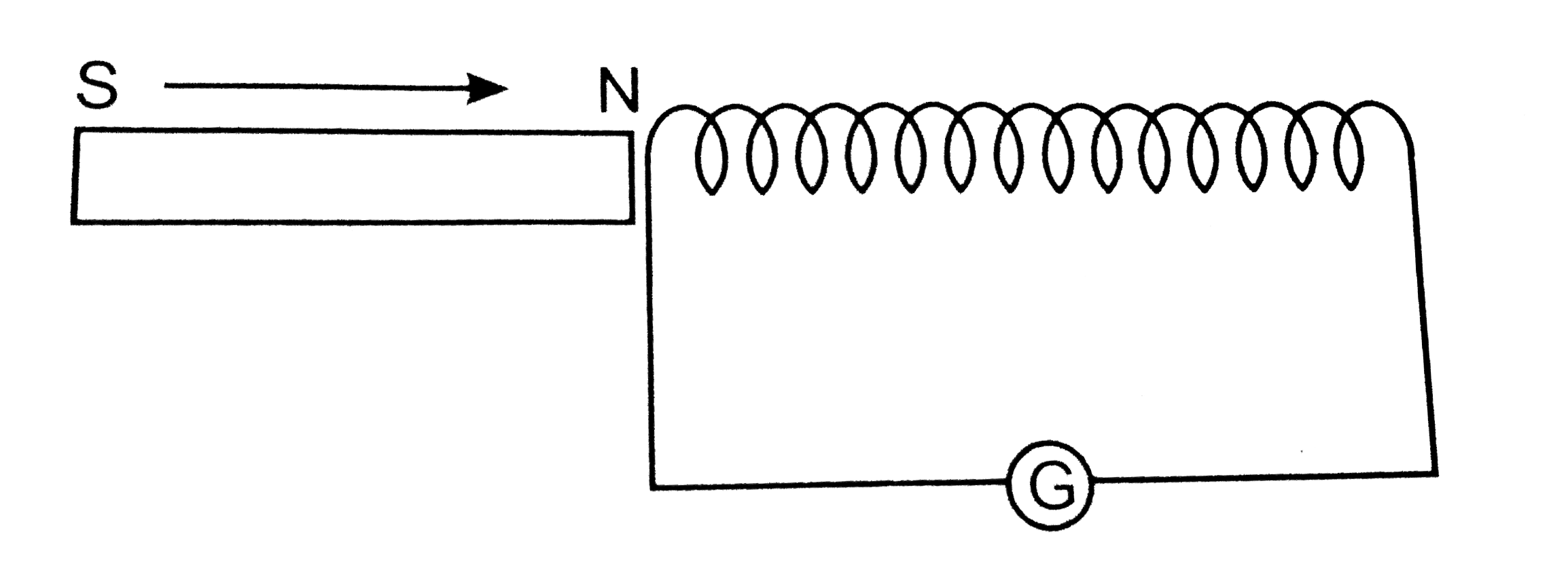
A magnet is brought towards a coil (i) speedily (ii) slowly then the induced e.m.f.//induced charge will be respectively

Options

A. more in first case/more in first case
B. more in first case/equal in both case
C. less in first case/more in second case
D. less in first case/equal in both case

Answer

B

Explanation

To solve the problem, we need to analyze the situation where a magnet is brought towards a coil at two different speeds: speedily and slowly. We will determine the induced electromotive force (e.m.f.) and the induced charge in each case.

1. Understanding Faraday's Law of Electromagnetic Induction:
- According to Faraday's law, the induced e.m.f. (ε) in a coil is given by the formula:
\( \varepsilon = -\frac{d\Phi}{dt} \)
where \( \Phi \) is the magnetic flux through the coil.

2. Magnetic Flux Change:
- Magnetic flux (\( \Phi \)) is defined as:
\( \Phi = B \cdot A \cdot \cos(\theta) \)
where \( B \) is the magnetic field strength, \( A \) is the area of the coil, and \( \theta \) is the angle between the magnetic field and the normal to the coil's surface.

3. Case (i): Magnet Brought Speedily:
- When the magnet is brought towards the coil speedily, the rate of change of magnetic flux (\( \frac{d\Phi}{dt} \)) is large. This results in a larger induced e.m.f.:
\( \varepsilon_{\text{speedy}} > \varepsilon_{\text{slow}} \)
- Therefore, the induced e.m.f. is greater when the magnet is brought speedily.

4. Case (ii): Magnet Brought Slowly:
- When the magnet is brought towards the coil slowly, the rate of change of magnetic flux is smaller, leading to a smaller induced e.m.f.:
\( \varepsilon_{\text{slow}} < \varepsilon_{\text{speedy}} \)

5. Induced Charge Calculation:
- The induced charge (Q) can be calculated using the formula:
\( Q = \frac{\varepsilon \cdot t}{R} \)
where \( R \) is the resistance of the coil, and \( t \) is the time for which the e.m.f. acts.
- Since the charge depends on the e.m.f. and the time, we need to consider the time taken in both cases.

6. Induced Charge for Both Cases:
- In the case of a speedy approach, the time taken is shorter, but the induced e.m.f. is higher. In the case of a slow approach, the time taken is longer, but the induced e.m.f. is lower.
- However, the total induced charge will be the same in both cases because the product of e.m.f. and time will yield the same result:
\( Q_{\text{speedy}} = Q_{\text{slow}} \)

Conclusion:
- Induced e.m.f. when the magnet is brought speedily: Greater
- Induced e.m.f. when the magnet is brought slowly: Lesser
- Induced charge in both cases: Equal

Final Answer:
- Induced e.m.f.: Greater (speedily), Lesser (slowly)
- Induced charge: Equal in both cases