The average velocity of molecules of a gas of molecular weight (M) at temperature (T) is
√3pp
√γpp
√2pp
√8pπp
The correct Answer is:D
Average speedof molecfule is the arithmetic mean of speed of molecules in a gas at given temperatures is
vav=v1+v2+v3+...N
From kinetic theory of gases,
√8pπp=√8RTπM=√8π=KTM
Topper's Solved these Questions
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Check point 14.4
25 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - A Tacking it together
55 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Check point 14.2
20 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective
8 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Subjective
9 Videos
Similar Questions
The average velocity of the molecules in a gas in equilibrium is
View SolutionRoot mean square velocity of gas molecules is 300m/sec. The r.m.s velocity of molecules of gas with twice the molecular weight and half the absolute temperature is :
View SolutionThe average kinetic energy of a molecule of a gas at absolute temperature T is proportional to
View SolutionExpress the average kinetic energy per mole of a monoatomic gas of molar mass M, at temperature T K in terms of the average speed of the molecules Uavg :
View SolutionThe ratio of root mean square velocity to average velocity of a gas molecule at a particular temperature is
View SolutionThe ratio of root mean square velocity of average velocity of a gas molecule at a particular temperture is
View SolutionThe average velocity of gas molecules is 400 m/sec calculate its rms velocity at the same temperature.
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
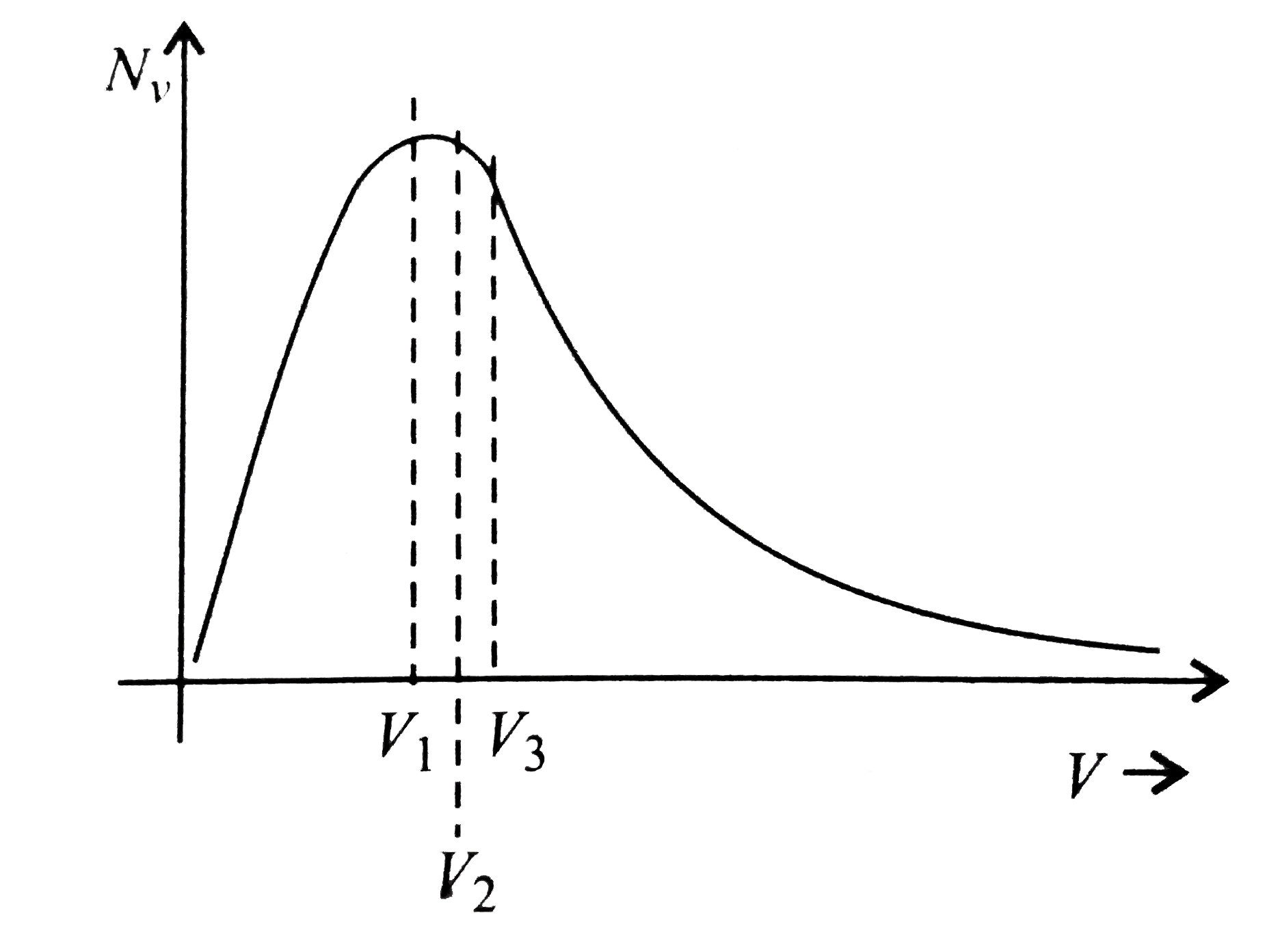
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of a are
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
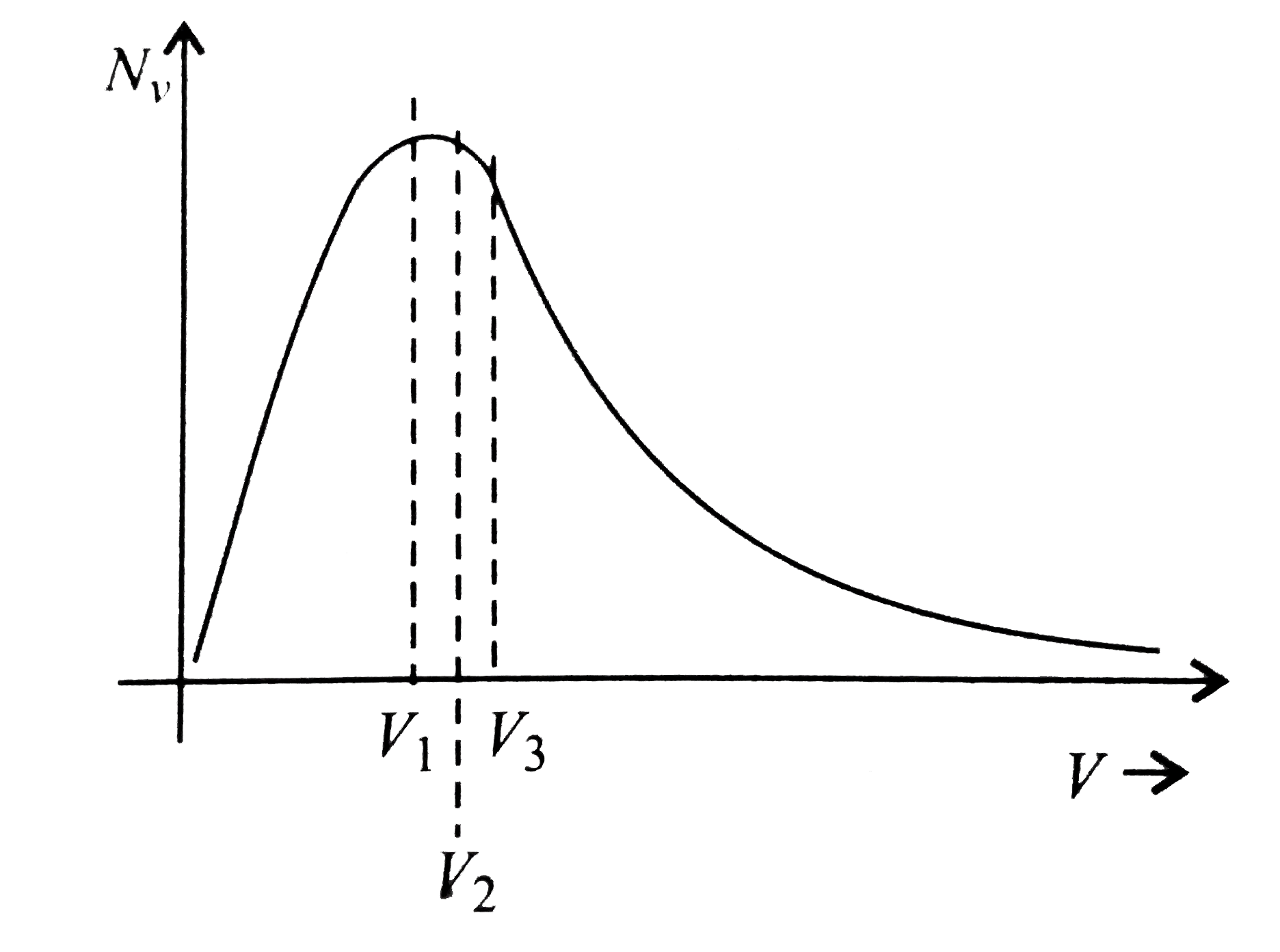
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of b are
View SolutionIf the average kinetic energy of a molecule of hydrogen gas at 300 K is E , then the average kinetic energy of a molecule of nitrogen gas at the same temperature is
View Solution
