A wooden block of mass 8 kg is tied to a string attached to the bottome of the tank. In the equilibrium the block is completely immersed in water. If relative density of wood is 0.8 and g=10ms−2, the tension T, in the string is
120 N
100 N
80 N
20 N
The correct Answer is:D
To solve the problem, we need to find the tension T in the string holding a wooden block submerged in water. Here’s a step-by-step solution:
Step 1: Identify the forces acting on the block
In equilibrium, the forces acting on the block are:
- The buoyant force Fb acting upwards.
- The weight of the block W acting downwards.
- The tension T in the string acting downwards.
Step 2: Write the equilibrium condition
Since the block is in equilibrium, the sum of the upward forces must equal the sum of the downward forces:
Fb=W+T
Step 3: Calculate the weight of the block
The weight W of the block can be calculated using the formula:
W=m⋅g
where m=8kg (mass of the block) and g=10m/s2 (acceleration due to gravity).
W=8kg×10m/s2=80N
Step 4: Calculate the volume of the block
The relative density (specific gravity) of the wood is given as 0.8. This means the density of the wood ρb can be calculated as:
ρb=relative density×density of water=0.8×1000kg/m3=800kg/m3
Now, using the formula for density:
ρb=mV⟹V=mρb
Substituting the values:
V=8kg800kg/m3=0.01m3
Step 5: Calculate the buoyant force
The buoyant force Fb can be calculated using Archimedes' principle:
Fb=ρl⋅V⋅g
where ρl=1000kg/m3 (density of water).
Fb=1000kg/m3×0.01m3×10m/s2=100N
Step 6: Substitute values into the equilibrium equation
Now substituting Fb and W into the equilibrium equation:
100N=80N+T
Step 7: Solve for tension T
Rearranging the equation to solve for T:
T=100N−80N=20N
Final Answer
The tension T in the string is 20N.
---
In equilibrium, the forces acting on the block are:
- The buoyant force Fb acting upwards.
- The weight of the block W acting downwards.
- The tension T in the string acting downwards.
Since the block is in equilibrium, the sum of the upward forces must equal the sum of the downward forces:
Fb=W+T
The weight W of the block can be calculated using the formula:
W=m⋅g
where m=8kg (mass of the block) and g=10m/s2 (acceleration due to gravity).
W=8kg×10m/s2=80N
The relative density (specific gravity) of the wood is given as 0.8. This means the density of the wood ρb can be calculated as:
ρb=relative density×density of water=0.8×1000kg/m3=800kg/m3
Now, using the formula for density:
ρb=mV⟹V=mρb
Substituting the values:
V=8kg800kg/m3=0.01m3
The buoyant force Fb can be calculated using Archimedes' principle:
Fb=ρl⋅V⋅g
where ρl=1000kg/m3 (density of water).
Fb=1000kg/m3×0.01m3×10m/s2=100N
Now substituting Fb and W into the equilibrium equation:
100N=80N+T
Rearranging the equation to solve for T:
T=100N−80N=20N
The tension T in the string is 20N.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A silver block of mass 3.1 kg is connected to a string and is then immersed in a liquid of relative density 0.82 . Find the tension in the string , if relative density of silver is 10.5
View SolutionA block of silver of mass 4kg hanging from a string is immersed in a liquid of relative density 0.72. If relative density of silver is 10, then tension in the string will be
View SolutionA block of silver of mass 4kg hanging from a string is immersed in a liquid of relative density 0.72. If relative density of silver is 10, then tension in the string will be
View SolutionCalculate the volume of wood of mass 6000 kg, when density of wood is 0.8 g cm−3
View SolutionA solid wooden cone has been supported by a string inside water as shown in the figure. The radius of the circular base of the cone is R and the volume of the cone is V. In equilibrium the base of the cone is at a depth H below the water surface. Density of wood is d(<ρ, density of water) Then tension in the string is
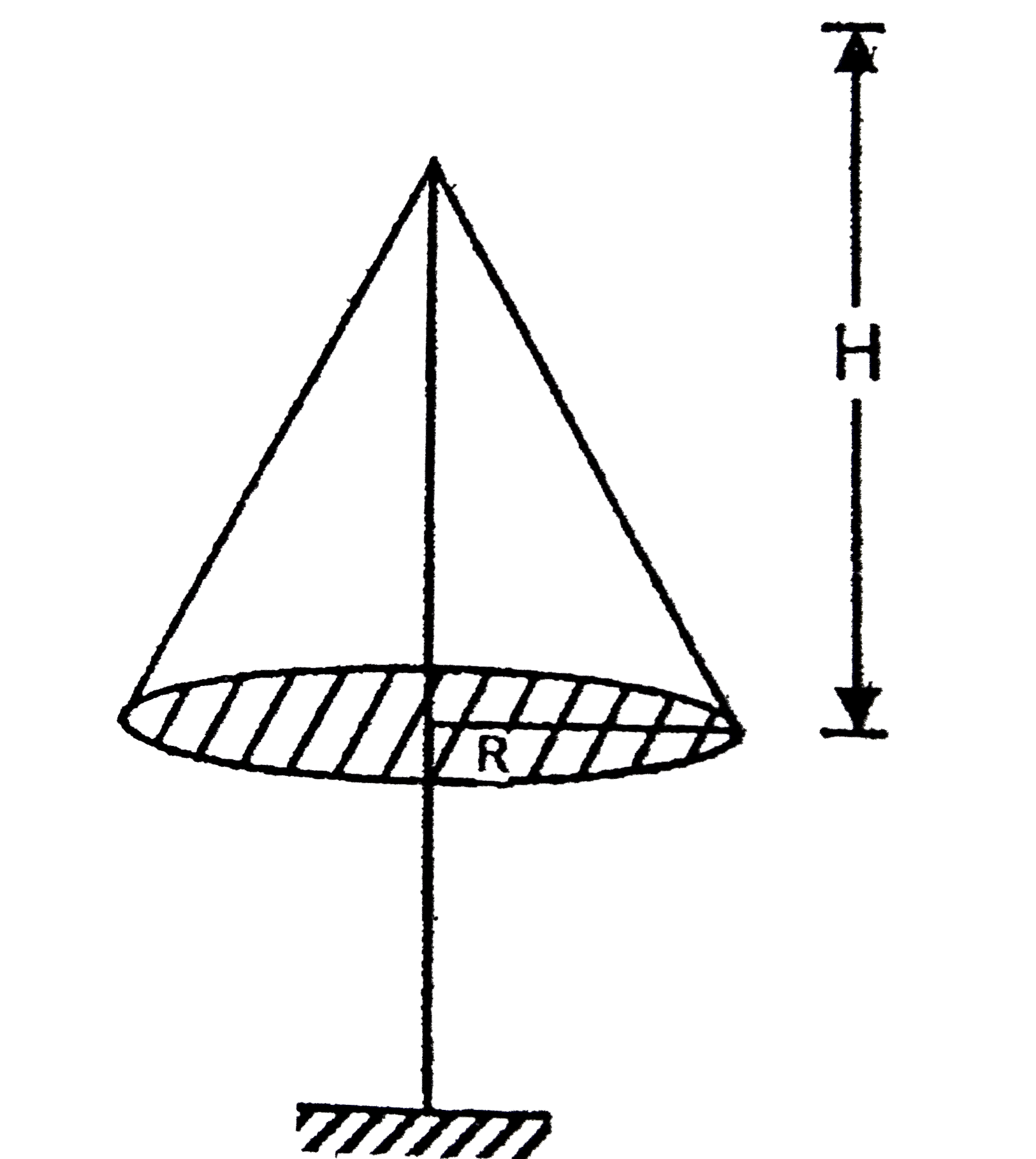
View SolutionA block of wood weighing 71.2N and of specific gravity 0.75 is tied by a string to the bottom of a tank of water in order to have the block totally immersed, What is the tension in the string?
View SolutionA metallic sphere of mass 3 kg in air is held by a string so as to be completely immersed in a liquid of relative density 0.8. The relative density of metallic sphere is 10. The tension in the string is :-
View SolutionThe mass of a wooden block is 56 g. If the density of wood is 0.8gcm−3 , find the volume of block.
View SolutionA block of mass 10 kg is suspended by three strings as shown in figure . Tension T2 is

View SolutionA block of wood of mass 24 kg floats on water. The volume of wood is 0.032m3 Find
a.the volume of block below the surface of water,
b.the density of wood.
(Denstiy of water =1000kgm−3)
View Solution
