The correct curve between the height or depression h of liquid in a capillary tube and its radius is
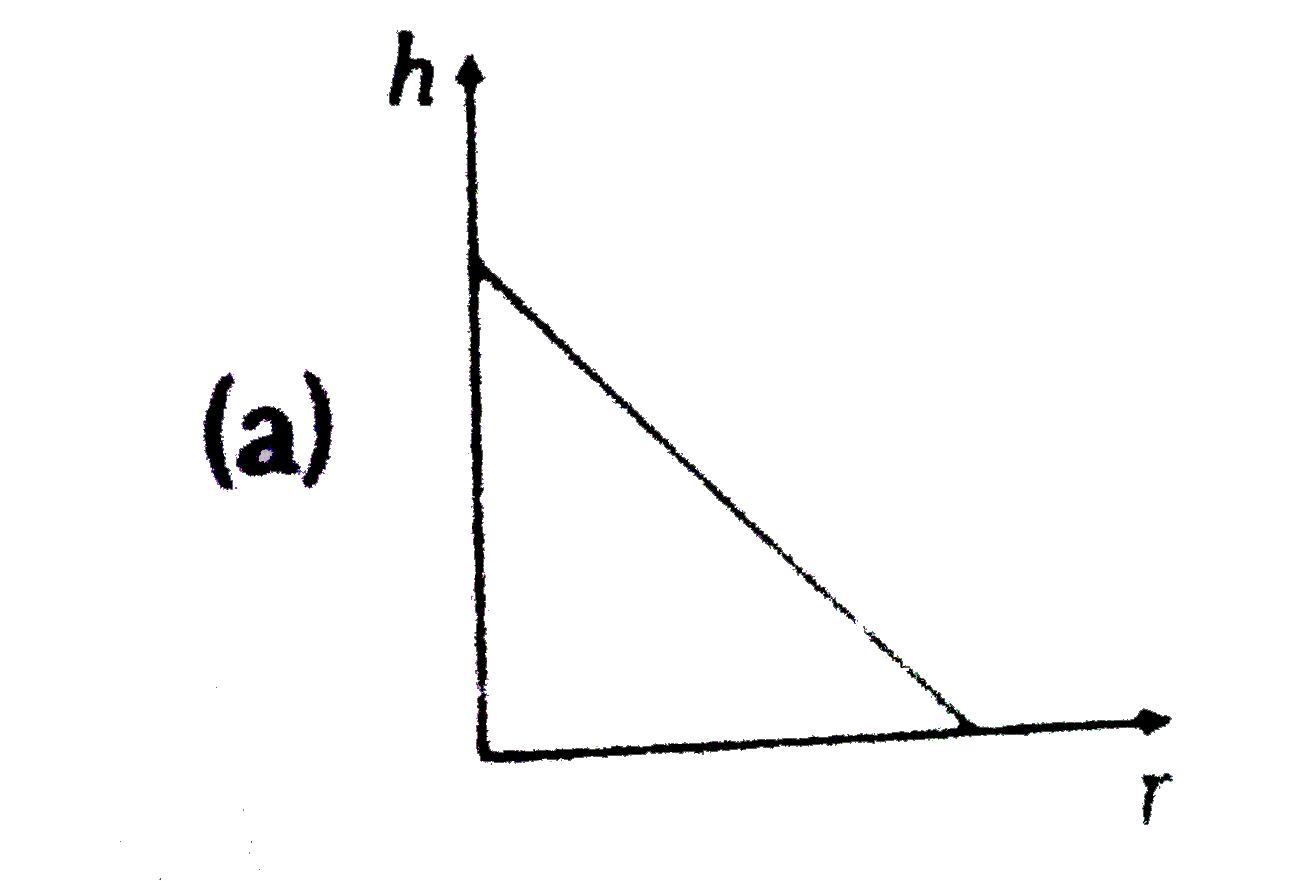
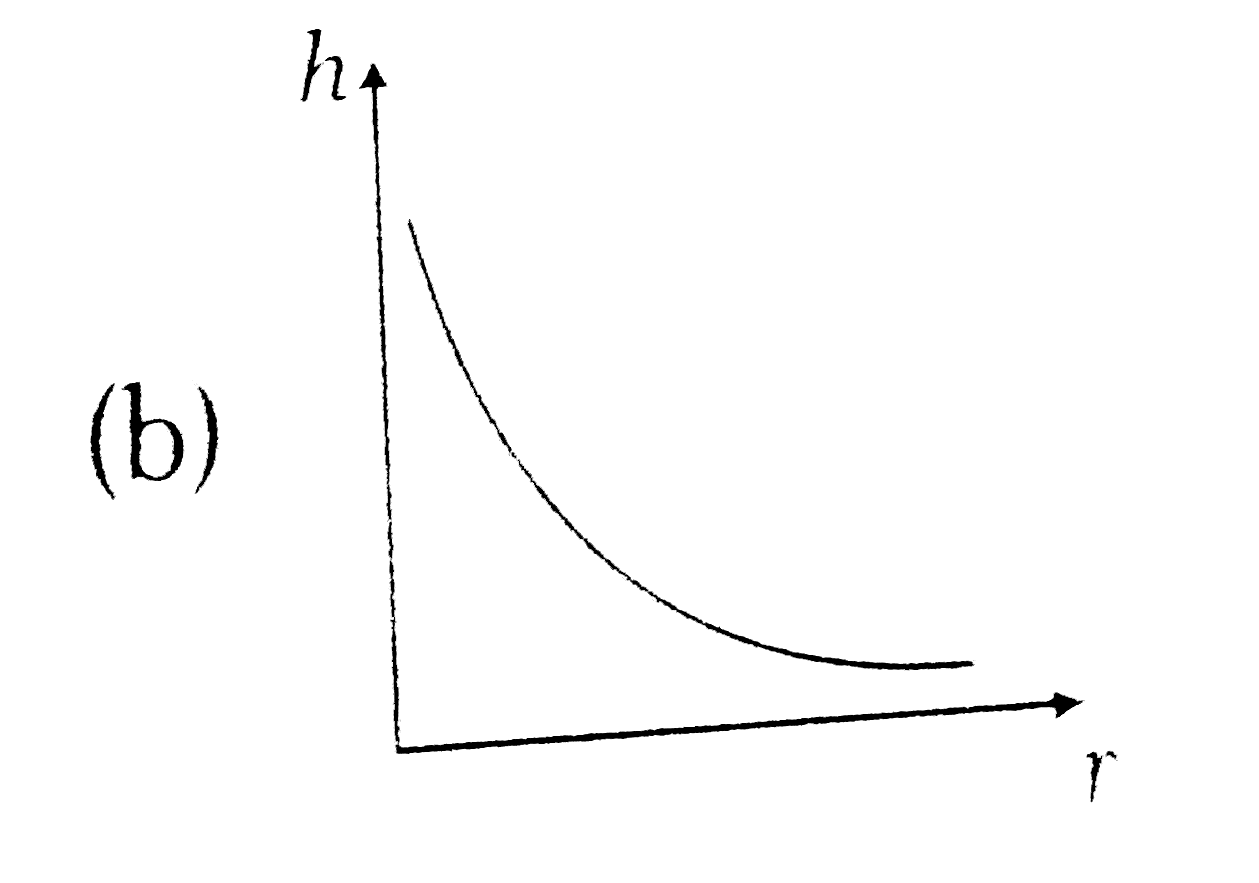
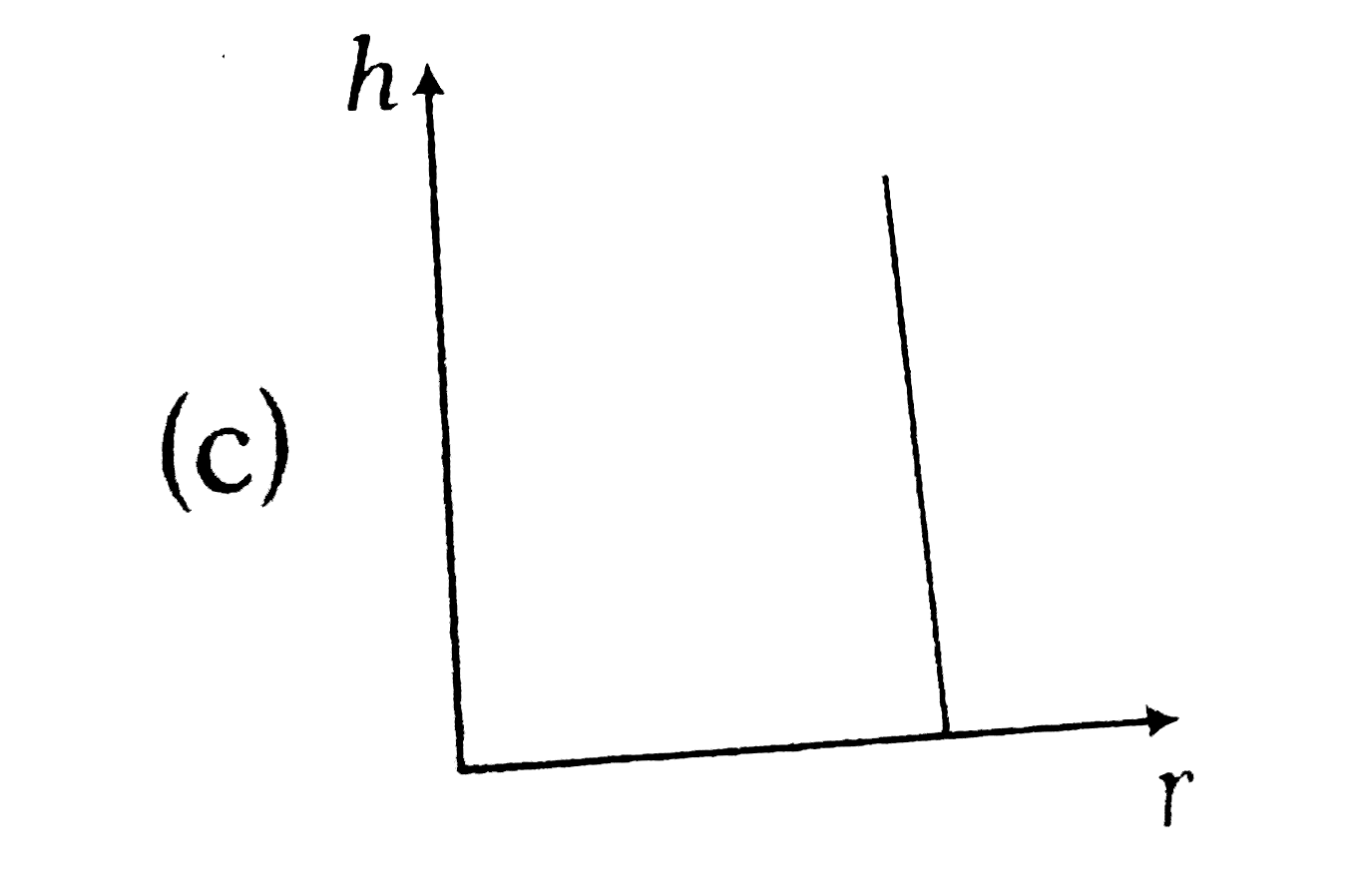
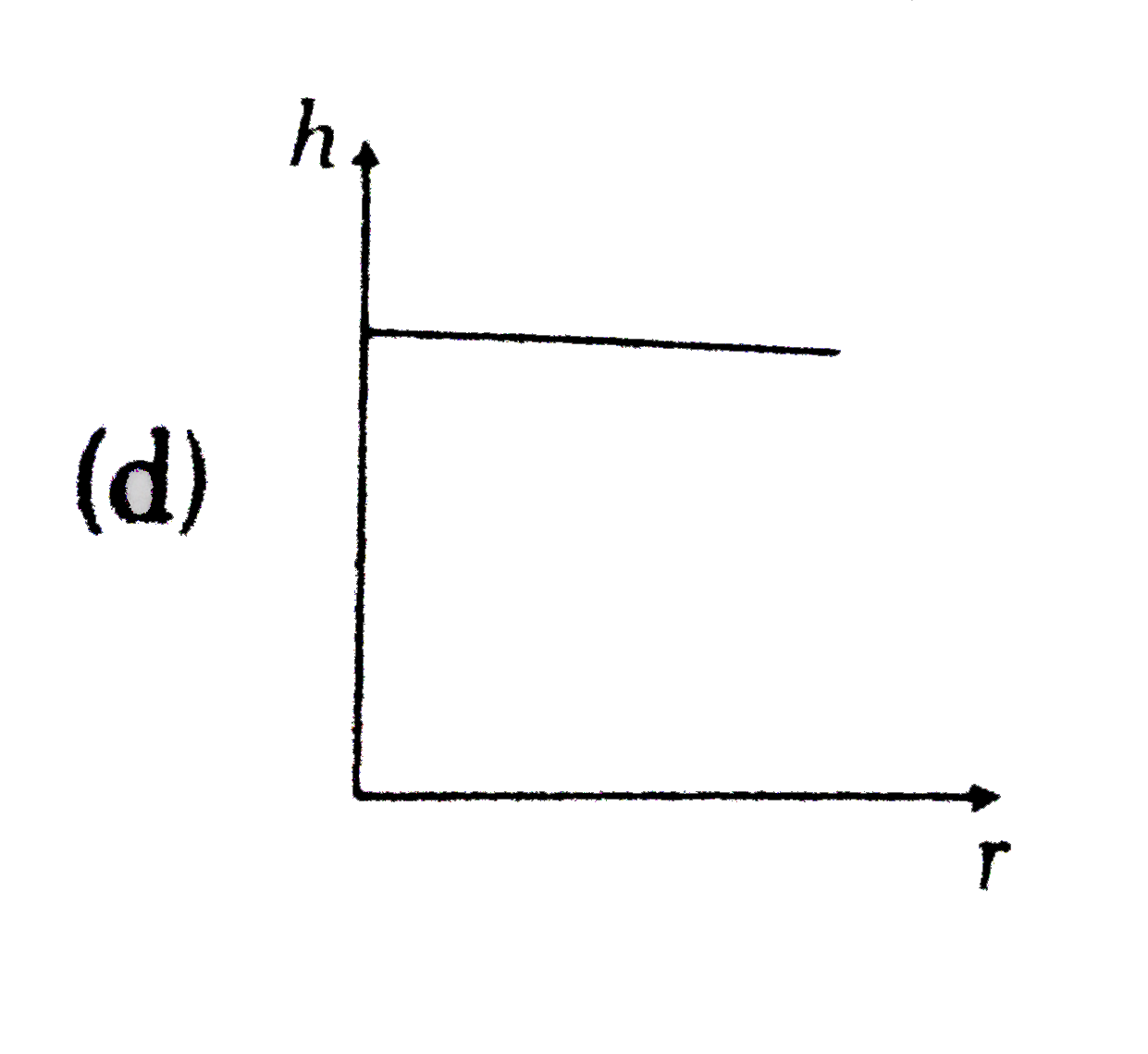
The correct Answer is:B
To solve the question regarding the relationship between the height of liquid depression h in a capillary tube and its radius r, we can follow these steps:
Step 1: Understand Capillary Action
Capillary action is the ability of a liquid to flow in narrow spaces without the assistance of external forces. It occurs due to the adhesive and cohesive forces between the liquid and the solid surface of the tube.
Step 2: Use the Capillary Rise Formula
The height of capillary rise (or depression) can be expressed using the formula:
h=2Tcosθρgr
Where:
- h = height of the liquid column (capillary rise or depression)
- T = surface tension of the liquid
- θ = contact angle
- ρ = density of the liquid
- g = acceleration due to gravity
- r = radius of the capillary tube
Step 3: Analyze the Relationship
From the formula, we can see that h is inversely proportional to r:
h∝1r
This means that as the radius r of the capillary tube increases, the height h of the liquid column decreases.
Step 4: Identify the Correct Curve
Since h is inversely proportional to r, we can conclude that the relationship between h and r can be represented graphically as a hyperbola. Specifically, if you plot h against r, you will get a curve that decreases as r increases.
Conclusion
The correct curve between the height or depression h of the liquid in a capillary tube and its radius r is a hyperbolic curve, indicating that h decreases as r increases.
---
Capillary action is the ability of a liquid to flow in narrow spaces without the assistance of external forces. It occurs due to the adhesive and cohesive forces between the liquid and the solid surface of the tube.
The height of capillary rise (or depression) can be expressed using the formula:
h=2Tcosθρgr
Where:
- h = height of the liquid column (capillary rise or depression)
- T = surface tension of the liquid
- θ = contact angle
- ρ = density of the liquid
- g = acceleration due to gravity
- r = radius of the capillary tube
From the formula, we can see that h is inversely proportional to r:
h∝1r
This means that as the radius r of the capillary tube increases, the height h of the liquid column decreases.
Since h is inversely proportional to r, we can conclude that the relationship between h and r can be represented graphically as a hyperbola. Specifically, if you plot h against r, you will get a curve that decreases as r increases.
The correct curve between the height or depression h of the liquid in a capillary tube and its radius r is a hyperbolic curve, indicating that h decreases as r increases.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
The rise of a liquid in a capillary tube is due to :
View SolutionThe rise of a liquid in a capillary tube depends on
View SolutionThere is a depression in the surface of the liquid in a capillary when
View SolutionThe graph between the mass of liquid inside the capillary and radius of capillary is
View SolutionA liquid rises in a capillary tube when the angle of contact is:
View SolutionIf Q is the rate of flow of liquid through a capillary tube of length l and radius r at constant pressure P, then the rate of flow of liquid through a capillary tube when radius is reduced to one third and length of tube is doubled
View SolutionWhat do you mean by capillarity. Derive relation for the rise of liquid in a capillary tube on the basis of balancing force and explain the rise of liquid in a tube of insufficient length.
View SolutionA liquid of density ρ and surface tension σ rises in a capillary tube of diameter d. Angle of contact between the tube and liquid is zero. The weight of the liquid in the capillary tube is:
View SolutionIf a liquid neither rises nor depresses in a capillary then it means that
View Solution
A container is partially filled with a liquid of density ρ2 A capillary tube of radius r is vertically inserted in this liquid. Now another liquid of density ρ1(ρ1<ρ2) is slowly poured in the container to a height h as shown. There is only denser liquid in the capillary tube. The rise of denser liquid in the capillary tube is also h. Assuming zero contact angle, the surface tension of heavier liquid is
View Solution
