In order that the resultant path on superimposing two mutually perpendicular SHM be a circle, the conditions are that
the amplitudes on both SHM should be equal and they should have a phase difference of π2
the amplitude should be in the ratio 1:2 and the phase difference should be zero
the amplitude should be in the ratio 1:2 and the phase difference should be π2
the amplitudes should be equal and the phase difference should be zero
The correct Answer is:A
To determine the conditions under which the resultant path of two mutually perpendicular simple harmonic motions (SHM) is a circle, we can follow these steps:
1. Define the SHM Equations:
Let's consider two simple harmonic motions along the x and y axes:
- For the x-axis: x=Asin(ωt)
- For the y-axis: y=Acos(ωt)
2. Square and Add the Equations:
To find the resultant motion, we can square both equations and add them:
x2+y2=(Asin(ωt))2+(Acos(ωt))2
3. Use the Pythagorean Identity:
Applying the Pythagorean identity sin2(θ)+cos2(θ)=1:
x2+y2=A2(sin2(ωt)+cos2(ωt))=A2
4. Resultant Motion:
The equation x2+y2=A2 represents a circle with radius A. This shows that the resultant path is indeed a circle.
5. Conditions for Circular Motion:
- Same Amplitude: The amplitudes of both SHMs must be equal, i.e., Ax=Ay=A.
- Phase Difference: The phase difference between the two SHMs must be 90∘ or π2 radians. This means if one SHM is represented by sin(ωt), the other must be represented by cos(ωt).
Conclusion:
For the resultant path of two mutually perpendicular SHMs to be a circle, the conditions are:
- The amplitudes of both SHMs must be equal.
- The phase difference between the two SHMs must be 90∘ (or π2 radians).
Let's consider two simple harmonic motions along the x and y axes:
- For the x-axis: x=Asin(ωt)
- For the y-axis: y=Acos(ωt)
To find the resultant motion, we can square both equations and add them:
x2+y2=(Asin(ωt))2+(Acos(ωt))2
Applying the Pythagorean identity sin2(θ)+cos2(θ)=1:
x2+y2=A2(sin2(ωt)+cos2(ωt))=A2
The equation x2+y2=A2 represents a circle with radius A. This shows that the resultant path is indeed a circle.
- Same Amplitude: The amplitudes of both SHMs must be equal, i.e., Ax=Ay=A.
- Phase Difference: The phase difference between the two SHMs must be 90∘ or π2 radians. This means if one SHM is represented by sin(ωt), the other must be represented by cos(ωt).
For the resultant path of two mutually perpendicular SHMs to be a circle, the conditions are:
- The amplitudes of both SHMs must be equal.
- The phase difference between the two SHMs must be 90∘ (or π2 radians).
Similar Questions
The square of the resultant of two forces 4N and 3 N exceeds the square of the resultant of the two forces by 12 when they are mutually perpendicular. The angle between the vectors is
View SolutionIf eight distinct points can be found on the curve |x|+|y|=1 such that from eachpoint two mutually perpendicular tangents can be drawn to the circle x2+y2=a2, then find the range of a.
View SolutionForces F1andF2 act on a point mass in two mutually perpendicular directions. The resultant force on the point mass will be
View SolutionForces F1andF2 act on a point mass in two mutually perpendicular directions. The resultant force on the point mass will be
View SolutionAn iron rod of length 2l is sliding on two mutually perpendicular lines . Find the locus of the midpoint of the rod.
View SolutionThree identical spheres each of mass M are placed at corners of right angle triangle with mutually perpendicular sides equal to 2m. Taking point of intersection of two mutually perpendicular sides as origin find position vector center of mass
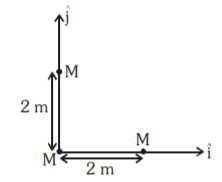
View SolutionA point moves in the xy-plane such that the sum of its distance from two mutually perpendicular lines is always equal to 3. The area of the locus of the point is
View SolutionThe resultant of two equal forces is 141.4N when they are mutually perpendicular. When they are inclined at an angle 120°, then the resultant force will be
View SolutionA tangent is drawn to each of the circles x2+y2=a2 and x2+y2=b2. Show that if the two tangents are mutually perpendicular, the locus of their point of intersection is a circle concentric with the given circles.
View SolutionA stick of length l slides with its ends on two mutually perpendicular lines. Find the locus of the middle point of the stick.
View Solution