An iron rod of length 2l is sliding on two mutually perpendicular lines . Find the locus of the midpoint of the rod.
The correct Answer is:x2+y2=l2
To find the locus of the midpoint of an iron rod of length 2L sliding on two mutually perpendicular lines, we can follow these steps:
1. Define the Coordinate System:
Let the two mutually perpendicular lines be the X-axis and Y-axis. The origin (0,0) is where these two axes intersect.
2. Position the Rod:
Consider the rod of length 2L sliding in such a way that its endpoints are on the axes. Let the endpoints of the rod be at points (0, A) on the Y-axis and (B, 0) on the X-axis.
3. Identify the Midpoint:
The midpoint M of the rod can be represented as M(X, Y). The coordinates of the endpoints of the rod are (0, A) and (B, 0).
4. Use the Midpoint Formula:
The coordinates of the midpoint M can be calculated using the midpoint formula:
M(X,Y)=(0+B2,A+02)=(B2,A2)
Therefore, we have:
X=B2andY=A2
5. Relate the Length of the Rod:
The length of the rod is given as 2L. The distance between the endpoints (0, A) and (B, 0) can be calculated using the distance formula:
Length=√(B−0)2+(0−A)2=√B2+A2
Setting this equal to the length of the rod, we have:
√B2+A2=2L
6. Square Both Sides:
Squaring both sides gives:
B2+A2=(2L)2=4L2
7. Substitute for B and A:
Since we have B=2X and A=2Y, substituting these into the equation gives:
(2X)2+(2Y)2=4L2
Simplifying this, we find:
4X2+4Y2=4L2
8. Divide by 4:
Dividing the entire equation by 4 results in:
X2+Y2=L2
Conclusion:
The locus of the midpoint of the rod is a circle with radius L centered at the origin (0,0).
Let the two mutually perpendicular lines be the X-axis and Y-axis. The origin (0,0) is where these two axes intersect.
Consider the rod of length 2L sliding in such a way that its endpoints are on the axes. Let the endpoints of the rod be at points (0, A) on the Y-axis and (B, 0) on the X-axis.
The midpoint M of the rod can be represented as M(X, Y). The coordinates of the endpoints of the rod are (0, A) and (B, 0).
The coordinates of the midpoint M can be calculated using the midpoint formula:
M(X,Y)=(0+B2,A+02)=(B2,A2)
Therefore, we have:
X=B2andY=A2
The length of the rod is given as 2L. The distance between the endpoints (0, A) and (B, 0) can be calculated using the distance formula:
Length=√(B−0)2+(0−A)2=√B2+A2
Setting this equal to the length of the rod, we have:
√B2+A2=2L
Squaring both sides gives:
B2+A2=(2L)2=4L2
Since we have B=2X and A=2Y, substituting these into the equation gives:
(2X)2+(2Y)2=4L2
Simplifying this, we find:
4X2+4Y2=4L2
Dividing the entire equation by 4 results in:
X2+Y2=L2
The locus of the midpoint of the rod is a circle with radius L centered at the origin (0,0).
Similar Questions
A rod of length l slides with its ends on two perpendicular lines. Find the locus of its midpoint.
View SolutionA rod of length l slides with its ends on two perpendicular lines. Find the locus of its midpoint.
View SolutionThe ends of a rod of length l move on two mutually perpendicular lines. Find the locus of the point on the rod which divides it in the ratio 1 : 2.
View SolutionA stick of length l slides with its ends on two mutually perpendicular lines. Find the locus of the middle point of the stick.
View SolutionA rod of length / slides with its ends on two perpendicular lines. Find the locus of its mid-point.
View SolutionThe ends of a rod of length l move on two mutually perpendicular lines. The locus of the point on the rod which divides it in the ratio 1 : 2 is
View SolutionA straight line segment of length/moves with its ends on two mutually perpendicular lines. Find the locus of the point which divides the line segment in the ratio 1:2
View Solution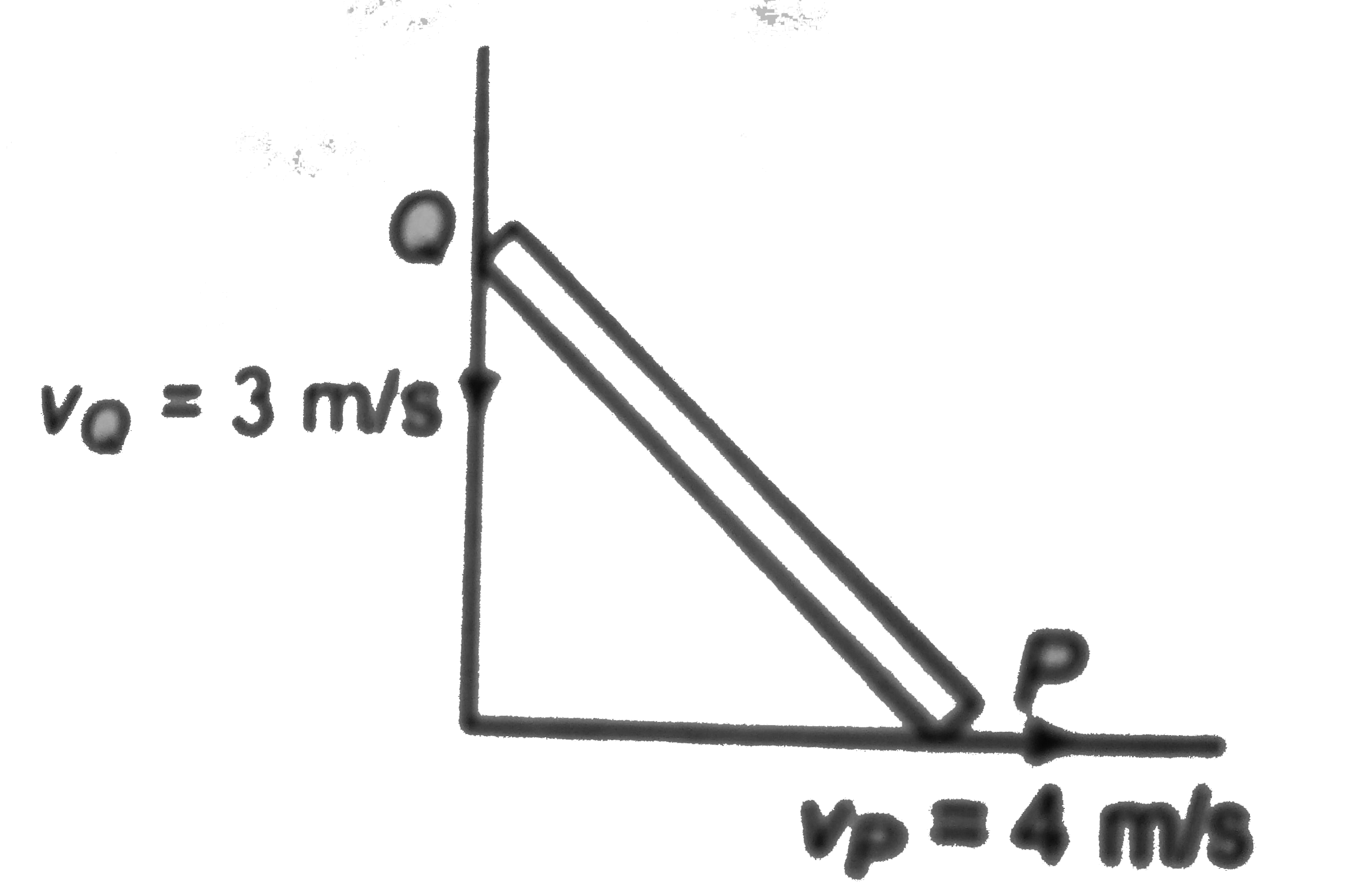
A uniform rod of mass m=2kg and length l=0.5m is sliding along two mutually perpendicular smooth walls with the two ends P and Q having velocities UP=4m/s and vQ=3m/s as shown then
View SolutionIf the extremities of a line segment of length l moves in two fixed perpendicular straight lines, then the locus of the point which divides this line segment in the ratio 1 : 2 is-
View SolutionThe ends of 20 cm long rod moves on two mutually perpendicular lines. If a point on this rod at 4 cm distance from end then from the eccentricity of the ellipse formed by moving that point.

View Solution

