In the case of sustained force oscillations the amplitude of oscillations
decreases linearly
decreases sinusodially
dereases exponentially
always remains constant
The correct Answer is:D
To solve the question regarding the amplitude of oscillations in the case of sustained force oscillations, we can follow these steps:
1. Understanding the System:
- We have a block attached to a spring with a spring constant k and mass M.
- The system experiences an external periodic force that drives it into oscillation.
2. Forces Acting on the System:
- The forces acting on the block include:
- The spring force, which is given by Hooke's Law as Fs=−kx (where x is the displacement from the equilibrium position).
- The damping force, which is proportional to the velocity of the block and is given as Fd=−bv (where b is the damping coefficient and v is the velocity).
- The external periodic force, which we can denote as Fext(t).
3. Net Force on the System:
- The net force acting on the block can be expressed as:
Fnet=Fext(t)+Fd+Fs
- This net force leads to the motion of the block.
4. Forced Oscillations:
- In sustained forced oscillations, the external force is applied in such a way that it compensates for the damping force and the spring force, allowing the system to oscillate at a constant amplitude.
5. Amplitude of Oscillation:
- The amplitude of oscillation in a forced oscillation system is determined by the balance between the driving force and the damping force.
- If the external force is constant and periodic, it can maintain a steady amplitude despite the damping effects.
6. Conclusion:
- In sustained force oscillations, the amplitude of oscillations remains constant over time. Therefore, the correct answer to the question is that the amplitude "always remains constant".
Final Answer:
The amplitude of oscillations in the case of sustained force oscillations always remains constant.
---
- We have a block attached to a spring with a spring constant k and mass M.
- The system experiences an external periodic force that drives it into oscillation.
- The forces acting on the block include:
- The spring force, which is given by Hooke's Law as Fs=−kx (where x is the displacement from the equilibrium position).
- The damping force, which is proportional to the velocity of the block and is given as Fd=−bv (where b is the damping coefficient and v is the velocity).
- The external periodic force, which we can denote as Fext(t).
- The net force acting on the block can be expressed as:
Fnet=Fext(t)+Fd+Fs
- This net force leads to the motion of the block.
- In sustained forced oscillations, the external force is applied in such a way that it compensates for the damping force and the spring force, allowing the system to oscillate at a constant amplitude.
- The amplitude of oscillation in a forced oscillation system is determined by the balance between the driving force and the damping force.
- If the external force is constant and periodic, it can maintain a steady amplitude despite the damping effects.
- In sustained force oscillations, the amplitude of oscillations remains constant over time. Therefore, the correct answer to the question is that the amplitude "always remains constant".
The amplitude of oscillations in the case of sustained force oscillations always remains constant.
Similar Questions
A mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200Nm−1 . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
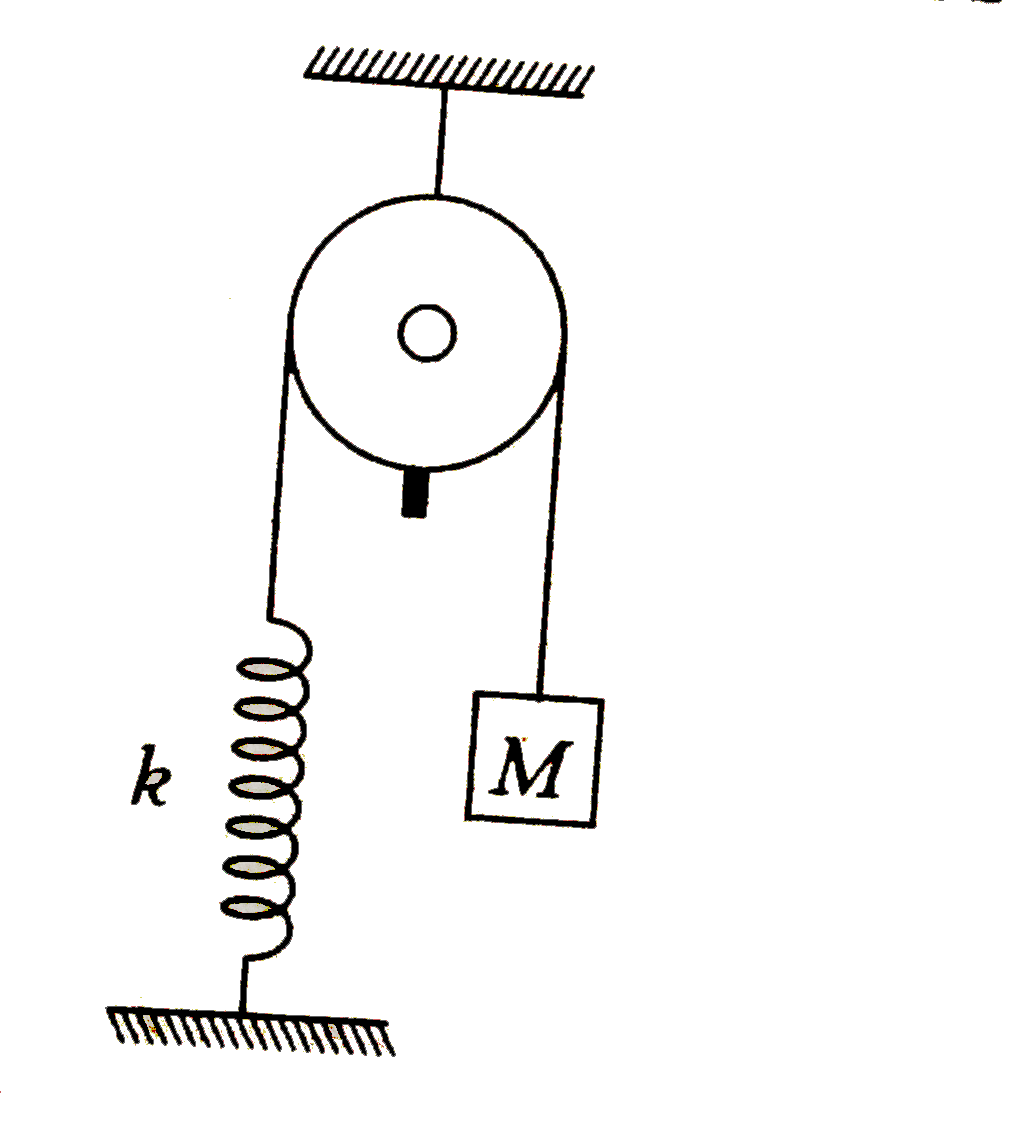
View SolutionA particle performing SHM is found at its equilibrium position at t = 1s and it is found to have a speed 0.25 = m//s at t=2s. If the period of oscillation is 6. Calculate amplitude of oscillation.
View Solution
Knowledge Check
At resonance, the amplitude of forced oscillations is
AminimumBmaximumCzeroDnone of theseIn case of force oscillations of a body
Adriving force is constant throughout.Bdriving force is to be applied only momentarilyCdriving force has to be periodic and continuousDdriving force is not required.
A body executing shm completes 120 oscillations per minute. If the amplitude of oscillations is 6 cm, find the velocity and acceleration of the particle when it is at a distance of 4 cm from the mean position?
View SolutionIn case of damped oscillation frequency of oscillation is
View SolutionA 2kg mass is attached to a spring of force constant 600N/m and rests on a smooth horizontal surface. A second mass of 1kg slides along the surface toward the first at 6m/s.
(a) Find the amplitude of oscillation if the masses make a perfectly inelastic collision and remain together on the spring. what is the period of oscillation ?
(b) Find the amplitude and period of oscillation if the collision is perfectly elastic.
( c) For each case , write down the position x as a function of time t for the mass attached to the spring, assuming that the collision occurs at time t=0. What is the impulse given to the 2kg mass in each case ?
View SolutionIn damped oscillations, the amplitude is reduced to one-third of its initial value a0 at the end of 100 oscillations. When the oscillator completes 200 oscillations ,its amplitude must be
View SolutionLength of a stretched wire is 2m. It is oscillating in its fourth overtone mode. Maximum amplitude of oscillations is 2mm. Find amplitude of oscillation at a distance of 0.2m from one fixed end.
View SolutionA particle executes simple harmonic oscillation with an amplitudes a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is
View Solution
