A wooden box of mass 8kg slides down an inclined plane of inclination 30∘ to the horizontal with a constant acceleration of 0.4ms−2 What is the force of friction between the box and inclined plane ? (g=10m/s2) .
12.2 BN
24.4 N
36.8 N
48.8 N
The correct Answer is:C
To solve the problem step by step, we will analyze the forces acting on the wooden box as it slides down the inclined plane.
Step 1: Identify the forces acting on the box
The forces acting on the box are:
1. The gravitational force (weight) acting downwards, W=mg.
2. The normal force (N) acting perpendicular to the inclined plane.
3. The frictional force (Ff) acting opposite to the direction of motion (up the incline).
Given:
- Mass of the box, m=8kg
- Acceleration due to gravity, g=10m/s2
- Inclination angle, θ=30∘
- Acceleration of the box, a=0.4m/s2
Step 2: Calculate the weight of the box
The weight of the box is calculated as:
W=mg=8kg×10m/s2=80N
Step 3: Resolve the weight into components
The weight can be resolved into two components:
1. The component parallel to the incline:
W∥=Wsinθ=80sin30∘=80×12=40N
2. The component perpendicular to the incline:
W_{\perpendicular} = W \cos \theta = 80 \cos 30^\circ = 80 \times \frac{\sqrt{3}}{2} = 40\sqrt{3} \, \text{N}
Step 4: Apply Newton's second law along the incline
According to Newton's second law, the net force acting on the box along the incline is equal to the mass times its acceleration:
Net force=m⋅a
The net force acting down the incline is given by:
W∥−Ff=m⋅a
Substituting the known values:
40N−Ff=8kg×0.4m/s2
40N−Ff=3.2N
Step 5: Solve for the frictional force
Rearranging the equation to find Ff:
Ff=40N−3.2N=36.8N
Conclusion
The force of friction between the box and the inclined plane is 36.8N.
---
The forces acting on the box are:
1. The gravitational force (weight) acting downwards, W=mg.
2. The normal force (N) acting perpendicular to the inclined plane.
3. The frictional force (Ff) acting opposite to the direction of motion (up the incline).
- Mass of the box, m=8kg
- Acceleration due to gravity, g=10m/s2
- Inclination angle, θ=30∘
- Acceleration of the box, a=0.4m/s2
The weight of the box is calculated as:
W=mg=8kg×10m/s2=80N
The weight can be resolved into two components:
1. The component parallel to the incline:
W∥=Wsinθ=80sin30∘=80×12=40N
2. The component perpendicular to the incline:
W_{\perpendicular} = W \cos \theta = 80 \cos 30^\circ = 80 \times \frac{\sqrt{3}}{2} = 40\sqrt{3} \, \text{N}
According to Newton's second law, the net force acting on the box along the incline is equal to the mass times its acceleration:
Net force=m⋅a
The net force acting down the incline is given by:
W∥−Ff=m⋅a
Substituting the known values:
40N−Ff=8kg×0.4m/s2
40N−Ff=3.2N
Rearranging the equation to find Ff:
Ff=40N−3.2N=36.8N
The force of friction between the box and the inclined plane is 36.8N.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns
7 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
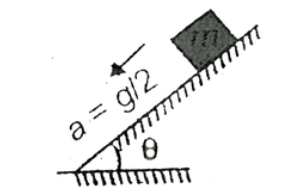
A block of mass m slides down a rough inclined plane with an acceleration g2
View SolutionA block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal. Calculate the acceleration of the block. The coefficient of friction between the block and surface is 0.6. (Take g=10m/s2)
View Solution
Knowledge Check
A body of mass 100 g is sliding from an inclined plane of inclination 30∘. What is the frictional force experienced if μ=1.7 ?
A1.7×√2×(1/√3)NB1.7×√3×(1/2)NC1.7×√3 ND1.7×√2×(1/3) N
A block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal . Calculate the acceleration of the block . The coefficient of friction between the block and surface is 0⋅6 ( Take g = 10m/s2)
View SolutionA block slides down on inclined plane (angle of inclination 60∘ ) with an accelration g/2 Find the coefficient friction

View SolutionA block slides down a frictionless, inclined plane that makes a 30∘ angle with the horizontal. Find the acceleration of this block.
View SolutionA block of mass 5.0 kg slides down an incline of inclination 300 and length 10 m. find the work done by the force of gravity.
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
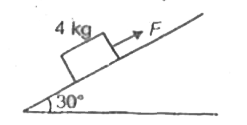
View SolutionA block of mass 4 kg is pulled along a smooth inclined plane of inclination 30∘ with constant velocity 3 m/s as shown, power delivered by the force is
View SolutionA box of mass 8kg placed on a rough inclined plane of inclination θ its downward motion can be prevented by applying an upward pull F and it can be made to slide upward appliying a force 2F .The coefficient of friction between the box and the inclined plane is
View Solution
