A coin is dropped in a lift. It takes time t1 to reach the floor when lift is stationary. It takes time t2 when lift is moving up with costant acceleration. Then
t1=t2
t1>t2
t2>t1
t1>>t2
The correct Answer is:B
To solve the problem, we need to analyze the motion of the coin in two different scenarios: when the lift is stationary and when the lift is moving upwards with constant acceleration.
1. Understanding the Scenario:
- When the lift is stationary, the only force acting on the coin is gravity.
- When the lift is moving upwards with constant acceleration, the effective acceleration acting on the coin changes.
2. Time Calculation when Lift is Stationary:
- Let the height from which the coin is dropped be h.
- The time taken t1 for the coin to reach the floor when the lift is stationary can be derived from the equation of motion:
h=12gt21
- Rearranging this gives:
t1=√2hg
3. Time Calculation when Lift is Moving Upwards:
- When the lift is moving upwards with a constant acceleration a, the effective acceleration acting on the coin becomes g+a (since the coin is falling downwards while the lift is accelerating upwards).
- The time taken t2 for the coin to reach the floor in this case can be calculated using the same equation of motion:
h=12(g+a)t22
- Rearranging this gives:
t2=√2hg+a
4. Comparing t1 and t2:
- We have:
t1=√2hgandt2=√2hg+a
- To compare t1 and t2, we can square both sides:
t21=2hgandt22=2hg+a
- Since g+a>g, it follows that:
2hg+a<2hg
- Therefore, we conclude that:
t22<t21⟹t2<t1
5. Conclusion:
- Thus, the time taken for the coin to reach the floor when the lift is moving upwards with constant acceleration is less than the time taken when the lift is stationary:
t1>t2
Final Answer:
The correct option is that t1 is greater than t2.
---
- When the lift is stationary, the only force acting on the coin is gravity.
- When the lift is moving upwards with constant acceleration, the effective acceleration acting on the coin changes.
- Let the height from which the coin is dropped be h.
- The time taken t1 for the coin to reach the floor when the lift is stationary can be derived from the equation of motion:
h=12gt21
- Rearranging this gives:
t1=√2hg
- When the lift is moving upwards with a constant acceleration a, the effective acceleration acting on the coin becomes g+a (since the coin is falling downwards while the lift is accelerating upwards).
- The time taken t2 for the coin to reach the floor in this case can be calculated using the same equation of motion:
h=12(g+a)t22
- Rearranging this gives:
t2=√2hg+a
- We have:
t1=√2hgandt2=√2hg+a
- To compare t1 and t2, we can square both sides:
t21=2hgandt22=2hg+a
- Since g+a>g, it follows that:
2hg+a<2hg
- Therefore, we conclude that:
t22<t21⟹t2<t1
- Thus, the time taken for the coin to reach the floor when the lift is moving upwards with constant acceleration is less than the time taken when the lift is stationary:
t1>t2
The correct option is that t1 is greater than t2.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns
7 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A coin is released inside a lift at a height of 2m from the floor of the lift. The height of the lift is 10 m. The lift is moving with an acceleration of 9m/s2downwards. The time after which the coin will strike with the lift is : (g=10m/s2)
View SolutionA person is standing at the floor of lift drops a coin The coin reaches the floor of lift in time t1. if elevator is stationary and in time t2, if it is moving uniformly then
View SolutionA spring balance is attached to the ceiling of a lift. A man hangs his bag on the spring and the spring reads 49N, when the lift is stationary. If the lift moves downward with an acceleration of 5m/22, the reading of the spring balance will be
View SolutionA spring balance is attached to the ceiling of a lift. A man hangs his bag on the spring and the spring reads 49N, when the lift is stationary. If the lift moves downward with an acceleration of 5m/22, the reading of the spring balance will be
View SolutionA spring balance is attached to the ceiling of a lift. A man hangs his bag on the spring and the spring reads 49N, when the lift is stationary. If the lift moves downward with an acceleration of 5m/22, the reading of the spring balance will be
View SolutionThe mass of man when standing on the lift is 60 kg. The weight when the lift is moving upwards with acceration 4.9ms−2 is
View SolutionThe apparent weight of a man in a lift is W1 when lift moves upwards with some acceleration and is W2 when it is accerating down with same acceleration. Find the true weight of the man and acceleration of lift .
View SolutionA lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string T1. Two masses of m1andm2 are connected with inextensible light string and tension in this string T2 as shown in figure. Read the questionbs carefully and answer
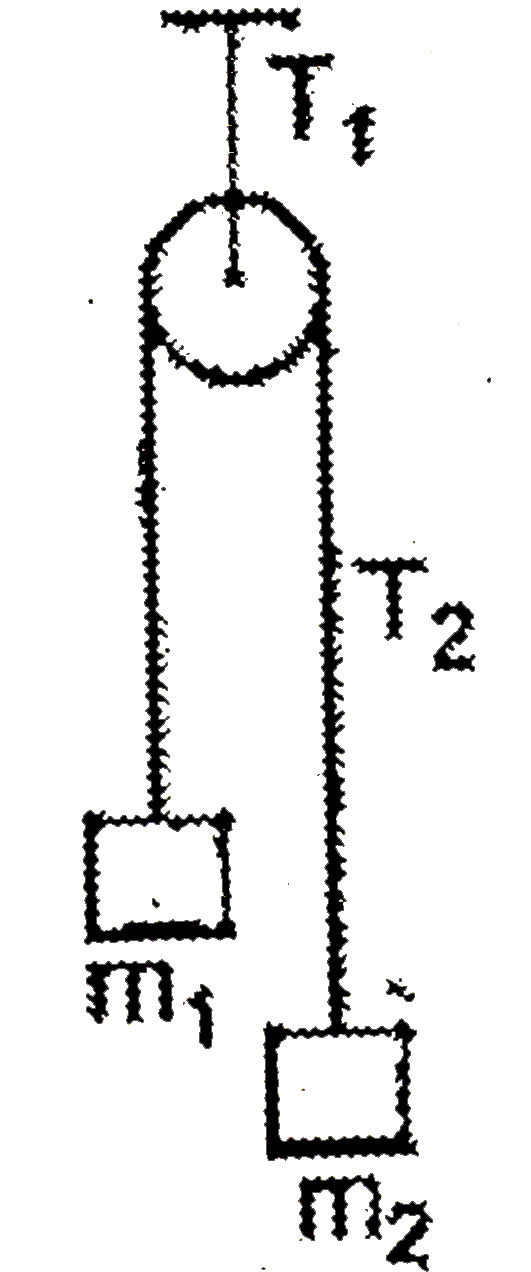
If m1=m2andm1 is moving at a certain instant with velocity v upward with respect to lift and the lift is moving in upward direction with constant acceleration (a<g) then speed of m2 with respect to lift :
View SolutionA ball after falling a distance of 5 meter rest hits elastically the floor of a lift and rebounds. At the time of impact the lift was moving up with a velocity of 1m/sec. The velocity with which the ball rebounds just after impact is : (g=10m/sec2)
View SolutionA body is thrown up in a lift with a velocity u relative to the lift, and returns to the lift in time t. Show that the lift's upward acceleration is (2u-gt)/t
View Solution
