A weight w is suspended from the midpoint of a rope, whose ends are at the same level. In order to make the rope perfectly horizontal, the force applied to each of its ends must be
less than w
equal to w
equal to 2w
infinitely large
The correct Answer is:D
To solve the problem of determining the force applied to each end of a rope in order to make it perfectly horizontal when a weight W is suspended from its midpoint, we can follow these steps:
1. Understand the Setup:
- We have a rope with a weight W suspended at its midpoint. The ends of the rope are at the same level.
- The goal is to make the rope perfectly horizontal.
2. Identify the Forces:
- When the rope is not horizontal, the tension T in the rope creates two components: a vertical component Tcosθ and a horizontal component Tsinθ.
- The vertical components of the tension from both sides must balance the weight W.
3. Set Up the Equilibrium Condition:
- Since the system is in equilibrium, the sum of the vertical forces must equal zero. Therefore, we can write:
2Tcosθ=W
- This equation states that the total upward force (from both sides of the rope) equals the downward force (the weight).
4. Solve for Tension T:
- Rearranging the equation gives:
T=W2cosθ
5. Consider the Case of a Perfectly Horizontal Rope:
- For the rope to be perfectly horizontal, the angle θ must approach 90∘.
- The cosine of 90∘ is 0, which leads to:
T=W2⋅0
- This implies that T approaches infinity.
6. Conclusion:
- Therefore, to make the rope perfectly horizontal, the force applied to each end must be infinitely large.
Final Answer:
The force applied to each of its ends must be infinitely large.
- We have a rope with a weight W suspended at its midpoint. The ends of the rope are at the same level.
- The goal is to make the rope perfectly horizontal.
- When the rope is not horizontal, the tension T in the rope creates two components: a vertical component Tcosθ and a horizontal component Tsinθ.
- The vertical components of the tension from both sides must balance the weight W.
- Since the system is in equilibrium, the sum of the vertical forces must equal zero. Therefore, we can write:
2Tcosθ=W
- This equation states that the total upward force (from both sides of the rope) equals the downward force (the weight).
- Rearranging the equation gives:
T=W2cosθ
- For the rope to be perfectly horizontal, the angle θ must approach 90∘.
- The cosine of 90∘ is 0, which leads to:
T=W2⋅0
- This implies that T approaches infinity.
- Therefore, to make the rope perfectly horizontal, the force applied to each end must be infinitely large.
The force applied to each of its ends must be infinitely large.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.3
20 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.4
20 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.1
20 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
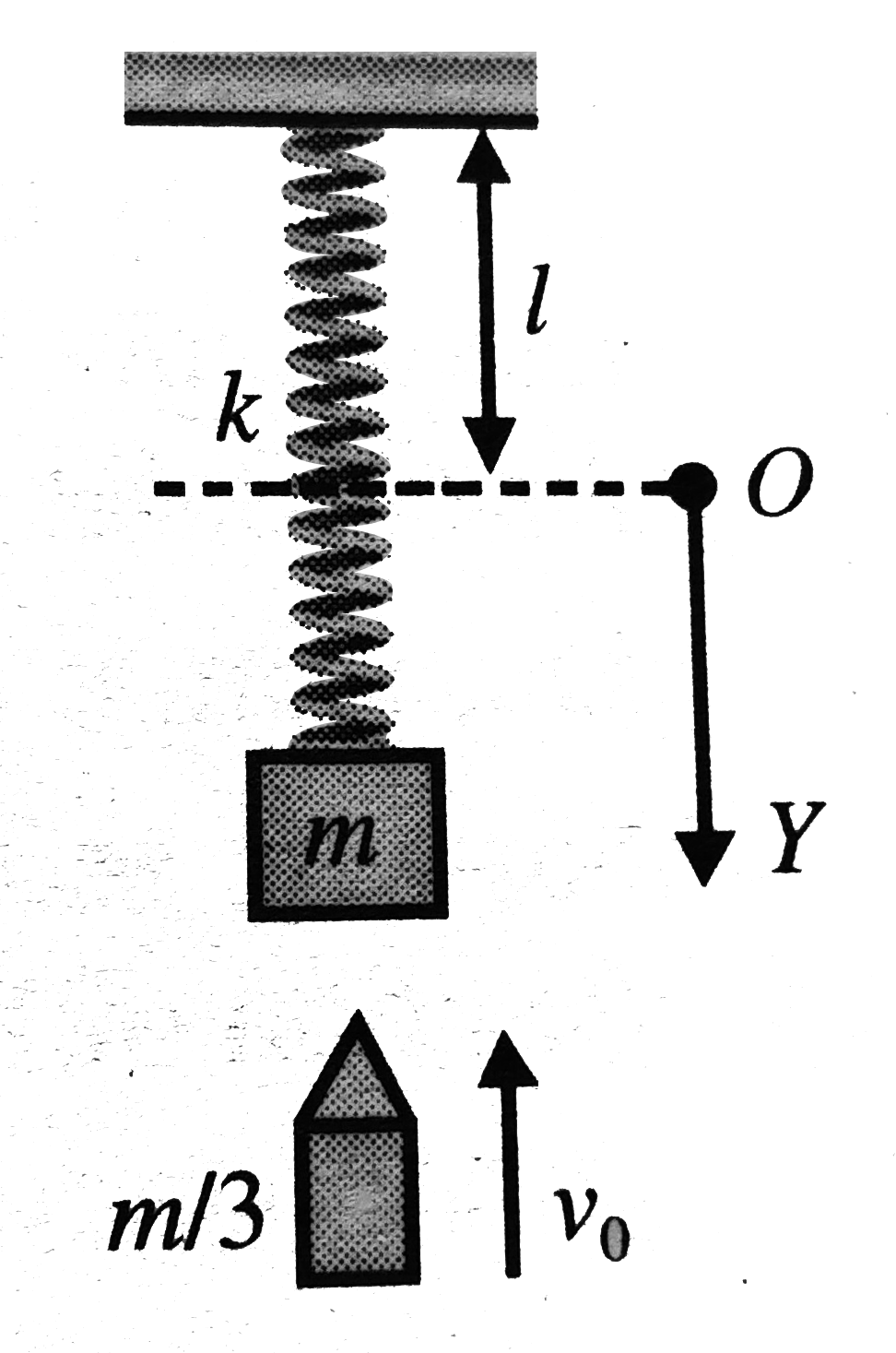
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The time taken by the block bullet system to move from y=mgk (initial equilibrium position) to y=0 (natural length of spring) is (A represents the amplitude of motion)
View SolutionA weight mg is suspended from the middle of a rope whose ends are at the same level. The rope is no longer horizontal. Find the minimum tenstion required to completely straighten the rope.
View Solution
Knowledge Check
A wire is suspended from the ceiling and stretched under the action of weight F suspended from its other end. The force exerted by the ceiling on it is equal and opposite to the weight.
ATensile stress at any cross section A of the wire is FA.BTensile stress at any cross section is zero.CTensile stress at any cross section A of the wire is 2FA.DTension at any cross section A of the wire is 2F.
A heavy rope is suspended from a rigid support A wave pulse is set up at the lower end, then
View SolutionA heavy rope is suspended from a rigid support A wave pulse is set up at the lower end, then
View SolutionA 10 kg body is suspended by a rope is pulled by means of a horizontal force to make 60° by rope to vertical. The horizontal force is
View SolutionThe Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
View SolutionA wire is suspended from the ceiling and stretched under the action of weight F suspended from its other end. The force exerted by the ceiling on it is equal and opposite to the weight.
View SolutionA uniform bar of square cross-section is lying along a frictionless horizontal surface. A horizontal force is applied to pull it from one of its ends then

View SolutionA mass M is suspended by a rope from a rigid support at A as shown in figure. Another rupe is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
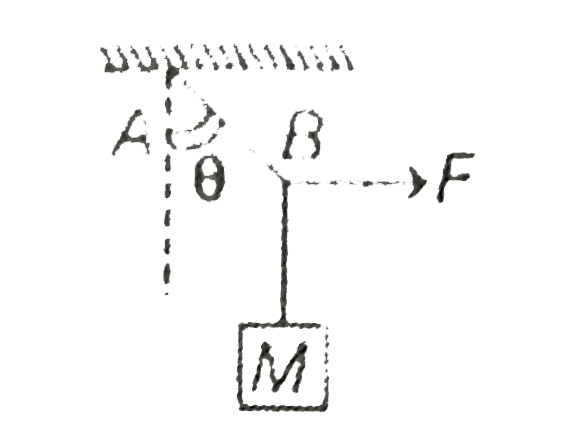
View Solution