An object is resting at the bottom of two strings which are inclined at an angle of 120∘ with each other. Each string can withstand a tension of 20 N. The maximum weight of the object that can be sustained without breaking the string is
10 N
20 N
20√2
40 N
The correct Answer is:B
To solve the problem, we need to determine the maximum weight of the object that can be sustained by the two strings without breaking them. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have two strings inclined at an angle of 120∘ with each other, supporting an object at the bottom. Each string can withstand a maximum tension of 20N.
Step 2: Identify Forces Acting on the Object
The forces acting on the object include:
- The gravitational force (weight) acting downwards, denoted as W (or mg).
- The tension forces in the strings acting upwards at an angle.
Step 3: Analyze the Tension Components
Since the strings are inclined, we need to resolve the tension into its components. Let T be the tension in each string. The angle between each string and the vertical is 60∘ (since 120∘ is the angle between the two strings, each string makes a 60∘ angle with the vertical).
Step 4: Calculate the Vertical Components of Tension
The vertical component of the tension from each string can be calculated as:
Tvertical=Tcos(60∘)
Since cos(60∘)=12, we have:
Tvertical=T⋅12
Step 5: Total Vertical Force from Both Strings
Since there are two strings, the total vertical force supporting the weight of the object is:
Ftotal=2Tcos(60∘)=2T⋅12=T
Step 6: Set Up the Equation
For the object to be in equilibrium (not moving), the total upward force must equal the downward force (weight of the object):
W=T
Step 7: Substitute the Maximum Tension
Given that each string can withstand a maximum tension of 20N, we substitute T=20N:
W=20N
Conclusion
The maximum weight of the object that can be sustained without breaking the strings is:
20N
We have two strings inclined at an angle of 120∘ with each other, supporting an object at the bottom. Each string can withstand a maximum tension of 20N.
The forces acting on the object include:
- The gravitational force (weight) acting downwards, denoted as W (or mg).
- The tension forces in the strings acting upwards at an angle.
Since the strings are inclined, we need to resolve the tension into its components. Let T be the tension in each string. The angle between each string and the vertical is 60∘ (since 120∘ is the angle between the two strings, each string makes a 60∘ angle with the vertical).
The vertical component of the tension from each string can be calculated as:
Tvertical=Tcos(60∘)
Since cos(60∘)=12, we have:
Tvertical=T⋅12
Since there are two strings, the total vertical force supporting the weight of the object is:
Ftotal=2Tcos(60∘)=2T⋅12=T
For the object to be in equilibrium (not moving), the total upward force must equal the downward force (weight of the object):
W=T
Given that each string can withstand a maximum tension of 20N, we substitute T=20N:
W=20N
The maximum weight of the object that can be sustained without breaking the strings is:
20N
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Check point 5.3
Explore 20 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Check point 5.4
Explore 20 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Check point 5.1
Explore 20 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
A particle of mass 100 g tied to a string is rotated along the circle of radius 0.5 m. The breaking tension of the string is 10 N. The maximum speed with which particle can be rotated without breaking the string is
View SolutionThe breaking tension of a string is 10 N. A particle of mass 0.1 kg tied to it is rotated along a horizontal circle of radius 0.5 meter. The maximum speed with which the particle can be rotated without breaking the string is
View SolutionA stone of mass of 16 kg is attached to a string 144 m long and is whirled in a horizontal circle. The maximum tension the string can withstand is 16 Newton . The maximum velocity of revolution that can be given to the stone without breaking it, will be
View SolutionA stone of mass 0.5 kg is attached to a string of length 2 m and is whirled in a horizontal circle. If the string can with stand a tension of 9N, the maximum velocity with which the stone can be whirled is:
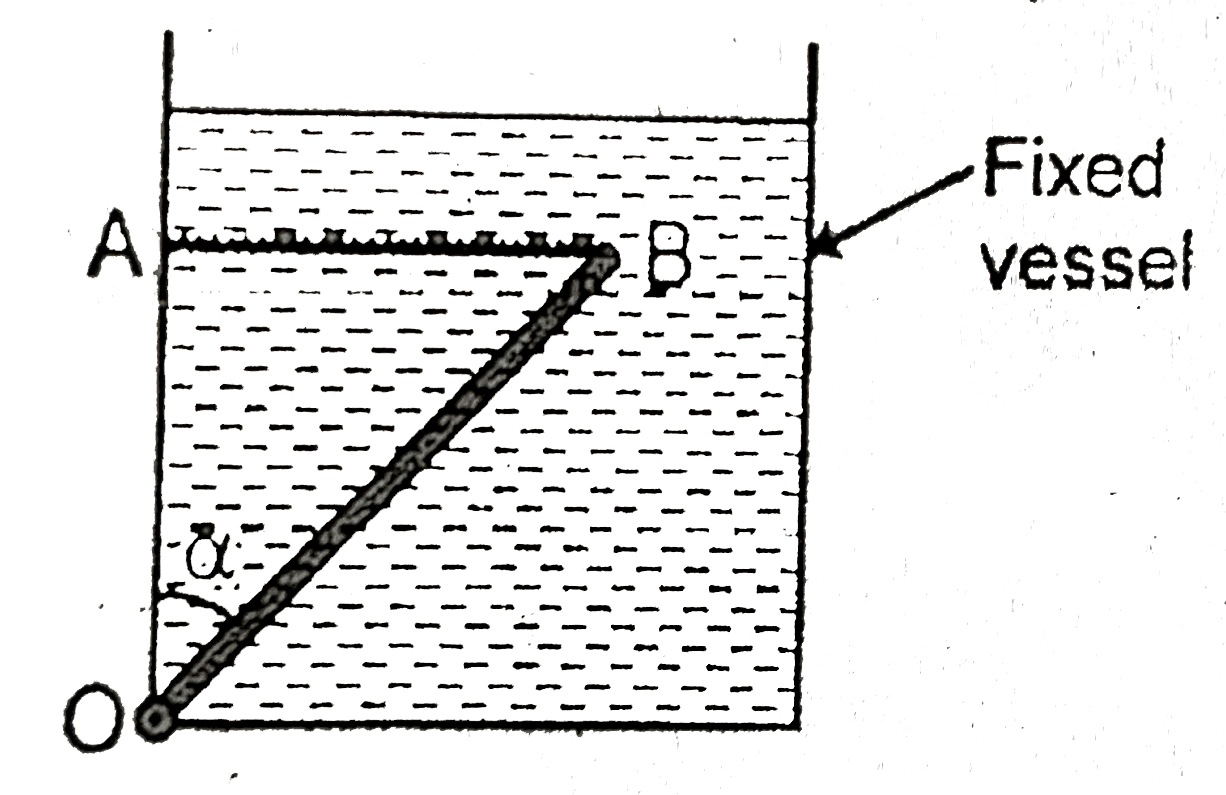
View SolutionA uniform rod OB of length 1m, cross-sectional areal 0.012m2 and relative density 2.0 is free to rotate about smooth hinge O in vertical plane. The rod is held with a horizontal string AB which can withstand a maximum tension of 45N. The rod and string system is kept in water as shown in figure. The maximum value of angle α which the rod can make with vertical without breaking the string is
View SolutionAn object is placed between two plane mirrors inclined at an angle to each other. If the number of images formed is 7 then the angle of inclination is -
View SolutionA small object is suspended at rest from two strings as shown in fig. The magnitude of the force exerted by each string on the object is 10√2N. Find the magnitude of the mass of the object.

View SolutionFind the weight of the suspended body if the tension in the diagonal string is 20 N

View SolutionA body of mass 0.5 kg is whirled with a velocity of 2ms−1 using 0.5 m length string which can be withstand a tension of 15 N, Neglecting the force of gravity on the body predict whether or not the string will break.
View SolutionA charged ball of mass 5.88×10−4 kg is suspended from two silk strings of equal lengths so that the strings are inclined at 60∘ with each other. Another ball carrying a charge which is equal in magnitude but opposite in sign of the first one is placed vertically below the first one at a distance of 4.2×10−2m. Due to this, the tension in the strings is doubled. Determine the charge on the ball and the tension in the strings after electrostatic interaction. (g=9.8m/s2)
View Solution