The driver of a train moving at a speed v1 sights another train at a disane d, ahead of him moving in the same direction with a slower speed v2. He applies the brakes and gives a constant teradation a to his train. Show that here will be no collision if d>(v1−v2)2/2a.
d>(υ1−υ22α)
d<(υ1−υ2)22α
d>(υ1−υ2)22α
None of these
The correct Answer is:C
To solve the problem, we need to analyze the motion of the two trains and derive the condition under which there will be no collision.
1. Understanding the Situation:
- Let the speed of the first train (the one applying brakes) be v1.
- Let the speed of the second train (the one ahead) be v2 (where v2<v1).
- The distance between the two trains is d.
- The first train applies brakes with a constant retardation a.
2. Relative Velocity:
- The relative velocity of the first train with respect to the second train is given by:
vrelative=v1−v2
3. Using the Equation of Motion:
- We can use the equation of motion which relates initial velocity, final velocity, acceleration, and distance:
v2=u2+2as
- Here, v will be the final velocity of the first train when it comes to rest, u is the initial relative velocity, a is the retardation (which will be negative), and s is the distance covered.
4. Setting Up the Equation:
- The first train will come to rest, so v=0.
- The initial relative velocity u is v1−v2.
- The retardation is −a (since it is deceleration).
- The distance s is d.
- Substituting these into the equation gives:
0=(v1−v2)2−2ad
5. Rearranging the Equation:
- Rearranging the above equation, we get:
2ad=(v1−v2)2
- Dividing both sides by 2a:
d=(v1−v2)22a
6. Condition for No Collision:
- For there to be no collision, the distance d must be greater than the distance calculated above:
d>(v1−v2)22a
Final Result:
Thus, we have shown that there will be no collision if:
d>(v1−v2)22a
- Let the speed of the first train (the one applying brakes) be v1.
- Let the speed of the second train (the one ahead) be v2 (where v2<v1).
- The distance between the two trains is d.
- The first train applies brakes with a constant retardation a.
- The relative velocity of the first train with respect to the second train is given by:
vrelative=v1−v2
- We can use the equation of motion which relates initial velocity, final velocity, acceleration, and distance:
v2=u2+2as
- Here, v will be the final velocity of the first train when it comes to rest, u is the initial relative velocity, a is the retardation (which will be negative), and s is the distance covered.
- The first train will come to rest, so v=0.
- The initial relative velocity u is v1−v2.
- The retardation is −a (since it is deceleration).
- The distance s is d.
- Substituting these into the equation gives:
0=(v1−v2)2−2ad
- Rearranging the above equation, we get:
2ad=(v1−v2)2
- Dividing both sides by 2a:
d=(v1−v2)22a
- For there to be no collision, the distance d must be greater than the distance calculated above:
d>(v1−v2)22a
Thus, we have shown that there will be no collision if:
d>(v1−v2)22a
Topper's Solved these Questions
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:(B) Meical entrance special format questions (Assertion and reason)
Explore 19 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:(B) Meical entrance special format questions (Mathch the columns)
Explore 6 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:Check point 3.7
Explore 15 Videos
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:Medical entrances gallery
Explore 19 Videos
- PROJECTILE MOTIONBook:DC PANDEY ENGLISHChapter:PROJECTILE MOTIONExercise:Level - 2 Subjective
Explore 10 Videos
Similar Questions
The driver of a train moving at 72kmh−1 sights another train moving at 4ms−1 on the same track and in the same direction. He instantly applies brakes to produces a retardation of 1ms−2. The minimum distance between the trains so that no collision occurs is
View SolutionAn express train is moving with a velocity v1. Its driver finds another train is movig on the same track in the same direction with velocity v2. To escape collision, driver applies a retardation a on the train. The minimum time of escaping collision be
View SolutionA train is moving at a constant speed V when its driverobserves another train in front of him on the same track and voing in the same direction with constant speed v. If the distance berween the trains is x. Trains is x then what should be the minimum retardation of the train so as to avoed collision?.
View SolutionA particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in they y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to :
View SolutionA car moving with speed v on a straight road can be stopped with in distance d on applying brakes. If same car is moving with speed 3v and brakes provide half retardation, then car will stop after travelling distance
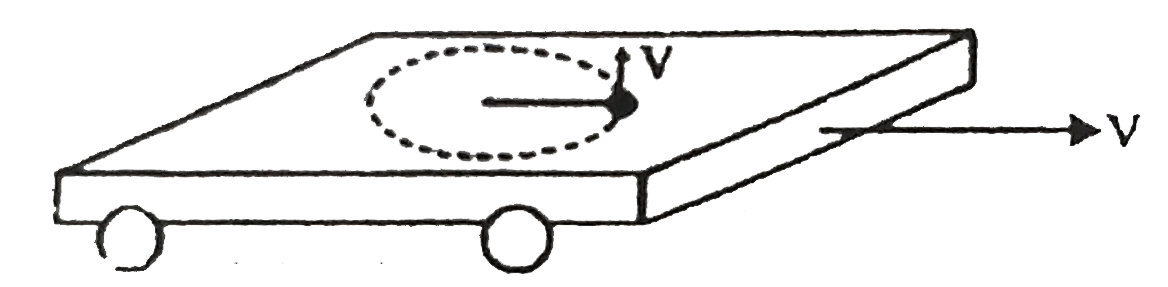
View SolutionOn a train moving along east with a constant speed v, a boy revolves a bob with string of length l on smooth surface of a train, with equal constant speed v relative to train. Mark the correct option(s).
View SolutionA train of mass M is moving on a circular track of radius R with constant speed v. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
View SolutionA train of mass M is moving on a circular track of radius R with constant speed v. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
View SolutionA train moving with uniform speed covers a distance of 120 m in 2 s. Calculate : (i) the speed of the train, (ii) the time it will take to cover 240 m.
View SolutionA man travels two-third part of his total distance with speed v1 and rest one-third part with speed v2. Find out the average speed of the man?
View Solution