If |A|=2 and |B|=4 and angle between then is 60∘ then |A-B|
√13
3√3
√3
2√3
The correct Answer is:D
To find the magnitude of the vector |A−B|, we can use the formula derived from the law of cosines. The formula for the magnitude of the difference of two vectors is given by:
|A−B|=√|A|2+|B|2−2|A||B|cos(θ)
Where:
- |A| is the magnitude of vector A
- |B| is the magnitude of vector B
- θ is the angle between vectors A and B
1. Identify the given values:
- |A|=2
- |B|=4
- θ=60∘
2. Substitute the values into the formula:
|A−B|=√22+42−2⋅2⋅4⋅cos(60∘)
3. Calculate |A|2 and |B|2:
- |A|2=22=4
- |B|2=42=16
4. Calculate cos(60∘):
- cos(60∘)=12
5. Substitute these values back into the equation:
|A−B|=√4+16−2⋅2⋅4⋅12
6. Simplify the expression:
|A−B|=√4+16−2⋅2⋅4⋅12=√4+16−8
|A−B|=√12
7. Further simplify √12:
√12=√4⋅3=2√3
8. Final answer:
|A−B|=2√3
Conclusion:
The magnitude of the vector |A−B| is 2√3.
- |A| is the magnitude of vector A
- |B| is the magnitude of vector B
- θ is the angle between vectors A and B
- |A|=2
- |B|=4
- θ=60∘
|A−B|=√22+42−2⋅2⋅4⋅cos(60∘)
- |A|2=22=4
- |B|2=42=16
- cos(60∘)=12
|A−B|=√4+16−2⋅2⋅4⋅12
|A−B|=√4+16−2⋅2⋅4⋅12=√4+16−8
|A−B|=√12
√12=√4⋅3=2√3
|A−B|=2√3
The magnitude of the vector |A−B| is 2√3.
Topper's Solved these Questions
Similar Questions
Angle between →a and →b is 60∘ then
View SolutionIf two adjacent sides of a cyclic quadrilateral aré 2 and 5 and the angle between them is 60°. If the third side is 3, then the remaining fourth side is (a) 2 (b) 3 (c) 4 (d) 5
View SolutionIf |A|=2,|B|=5 and |A×B|=8. Angle between A and B is acute, then (A.B) is
View SolutionIf |→a|=4,∣∣→b∣∣=2 and angle between →aand→bisπ6then(→a×→b)2 is (A) 48 (B) (→a)2 (C) 16 (D) 32
View SolutionIf A.B=A×B, then angle between A and B is
View SolutionThree vectors a(|a|≠0),b and c are such that a×b=3a×c, also |a|=|b|=1and|c|=13. If the angle between b and c is 60∘ and |b−3x|=λ|a|, then the value of λ is
View SolutionFind the magnitude of two vectors →aand →b having the same magnitude and such that the angle between them is 600and their scalar product is 12.
View SolutionFind the magnitude of each of the two vectors →a and →b having the same magnitude such that the angle between them is 60∘ and their scalar product is 92.
View SolutionFor what angle between A and B, |A+B|=|A−B| .
View SolutionIf |A|=2 and |B| = 4, then match the relation in Column I with the angle θ between A and B in Column II.
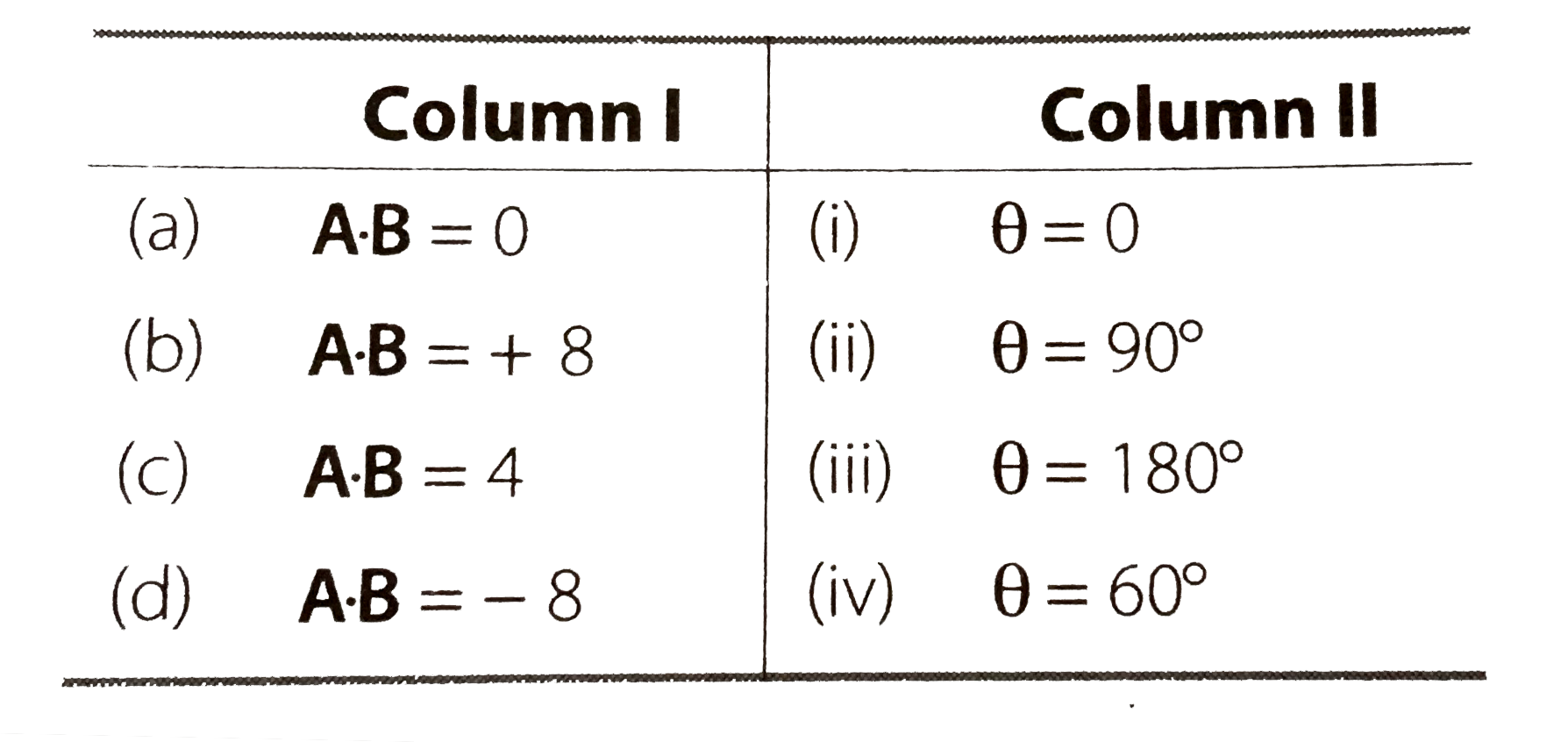
View Solution