For what angle between A and B, |A+B|=|A−B| .
To solve the problem, we need to find the angle θ between two vectors A and B such that the magnitudes of the vector sums and differences are equal, i.e., |A + B| = |A - B|.
1. Write the Magnitude Expressions:
We start with the expressions for the magnitudes of the vector sums and differences:
|A+B|=√A2+B2+2ABcosθ
|A−B|=√A2+B2−2ABcosθ
2. Set the Magnitudes Equal:
According to the problem, we need to set these two expressions equal:
√A2+B2+2ABcosθ=√A2+B2−2ABcosθ
3. Square Both Sides:
To eliminate the square roots, we square both sides:
A2+B2+2ABcosθ=A2+B2−2ABcosθ
4. Simplify the Equation:
By simplifying the equation, we can cancel out A2+B2 from both sides:
2ABcosθ=−2ABcosθ
5. Combine Like Terms:
Rearranging gives us:
2ABcosθ+2ABcosθ=0
4ABcosθ=0
6. Solve for Cosine:
Since A and B are non-zero vectors, we can divide both sides by 4AB:
cosθ=0
7. Determine the Angles:
The cosine of an angle is zero at:
θ=90∘orθ=270∘
Final Answer:
The angles between vectors A and B for which |A + B| = |A - B| are:
θ=90∘andθ=270∘
We start with the expressions for the magnitudes of the vector sums and differences:
|A+B|=√A2+B2+2ABcosθ
|A−B|=√A2+B2−2ABcosθ
According to the problem, we need to set these two expressions equal:
√A2+B2+2ABcosθ=√A2+B2−2ABcosθ
To eliminate the square roots, we square both sides:
A2+B2+2ABcosθ=A2+B2−2ABcosθ
By simplifying the equation, we can cancel out A2+B2 from both sides:
2ABcosθ=−2ABcosθ
Rearranging gives us:
2ABcosθ+2ABcosθ=0
4ABcosθ=0
Since A and B are non-zero vectors, we can divide both sides by 4AB:
cosθ=0
The cosine of an angle is zero at:
θ=90∘orθ=270∘
The angles between vectors A and B for which |A + B| = |A - B| are:
θ=90∘andθ=270∘
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 5.24videos
VECTORS
- BOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 5.34videos
VECTORS
- BOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery9videos
VECTORS
- BOOK - DC PANDEY ENGLISHCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Medical entrances gallery32videos
UNITS, DIMENSIONS & ERROR ANALYSIS
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
Similar Questions
Obtain the angle between A+B and A-B if A=2ˆi+3ˆjandB=ˆi−2ˆj.
View SolutionIf A.B=A×B, then angle between A and B is
View SolutionIf ∣∣→A+→B∣∣=∣∣→A∣∣=∣∣→B∣∣ then angle between A and B will be
View SolutionWhen a charged particle moving with velocity →V is subjected to a magnetic field of induction →B the force on it is non-zero. This implies that:
(1.)angle between v and B is necessery 90 ∘
(2.)angle between v and B can have any value other than 90 ∘
(3.)angle between v and B can have any value other than zero and 180 ∘
(4.)angle between v and B is either zero or 180 ∘View SolutionIf |A|=2 and |B| = 4, then match the relation in Column I with the angle θ between A and B in Column II.
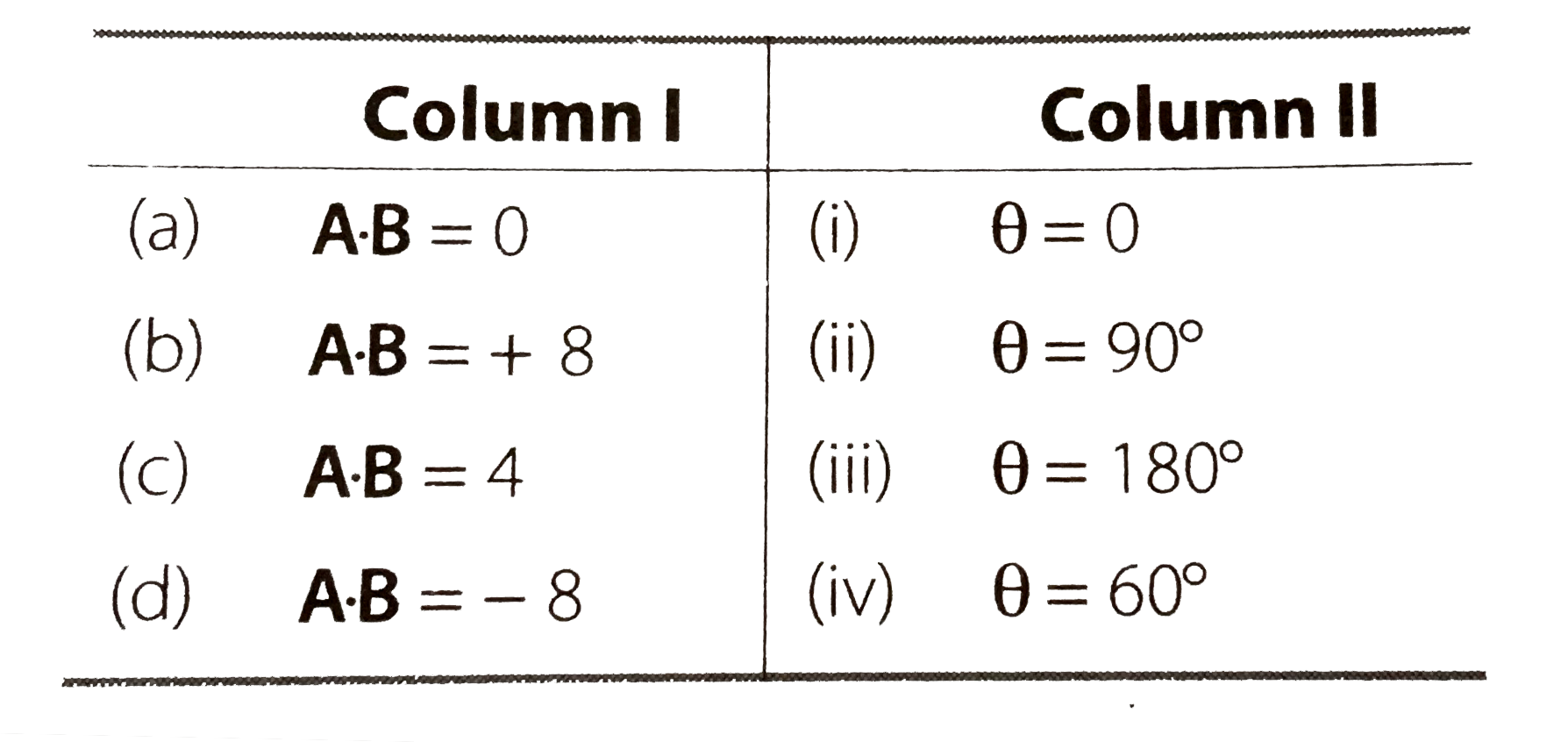 View Solution
View SolutionTwo vectors →A and →B are such that ∣∣→A+→B∣∣=∣∣→A−→B∣∣ then what is the angle between →Aand →B :-
View SolutionThe resultant of two vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between A and B is -
 View Solution
View SolutionIn the shown fig . 5.12 (a) , (b) and (c ) , find the angle between A and B .
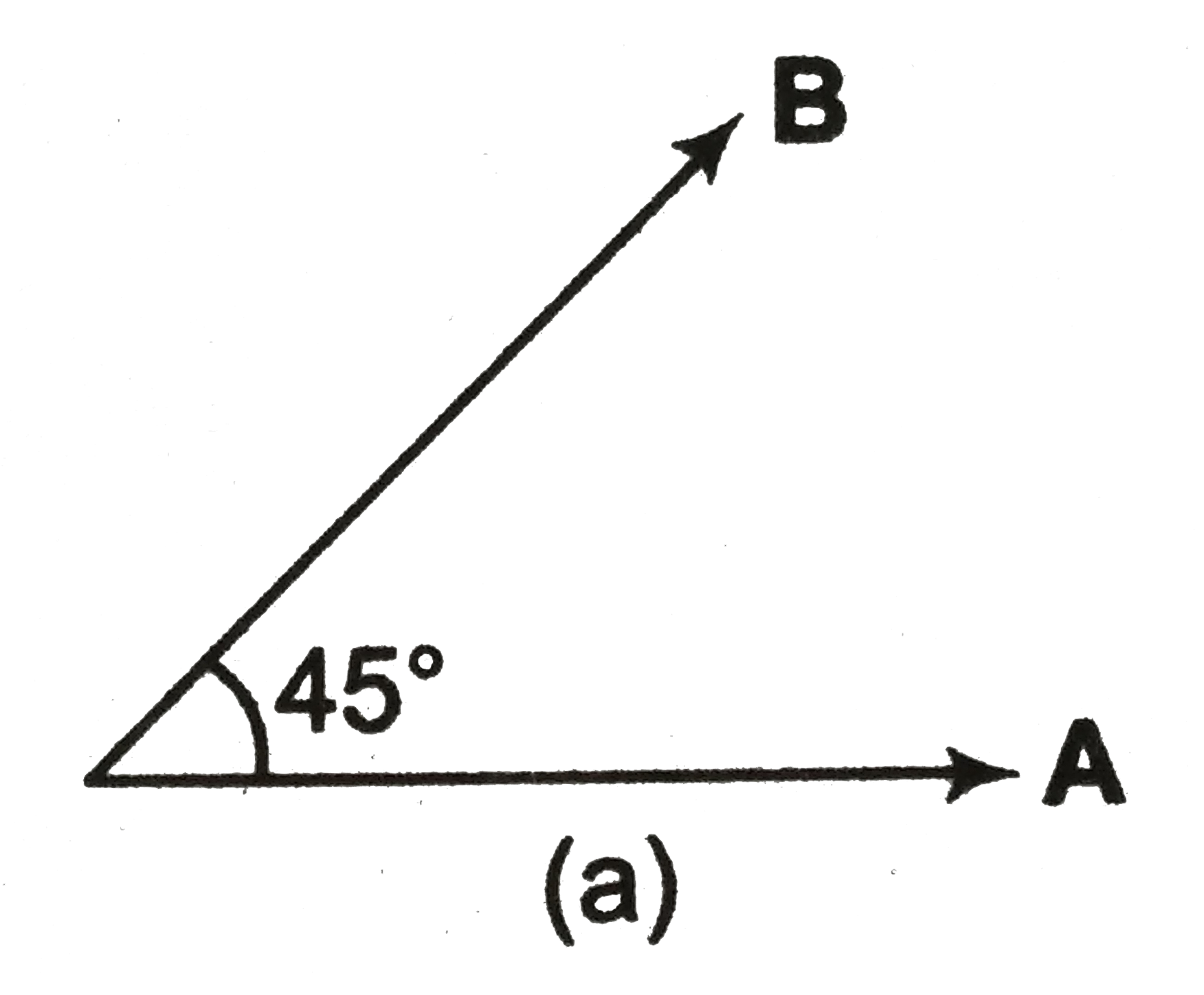
(b)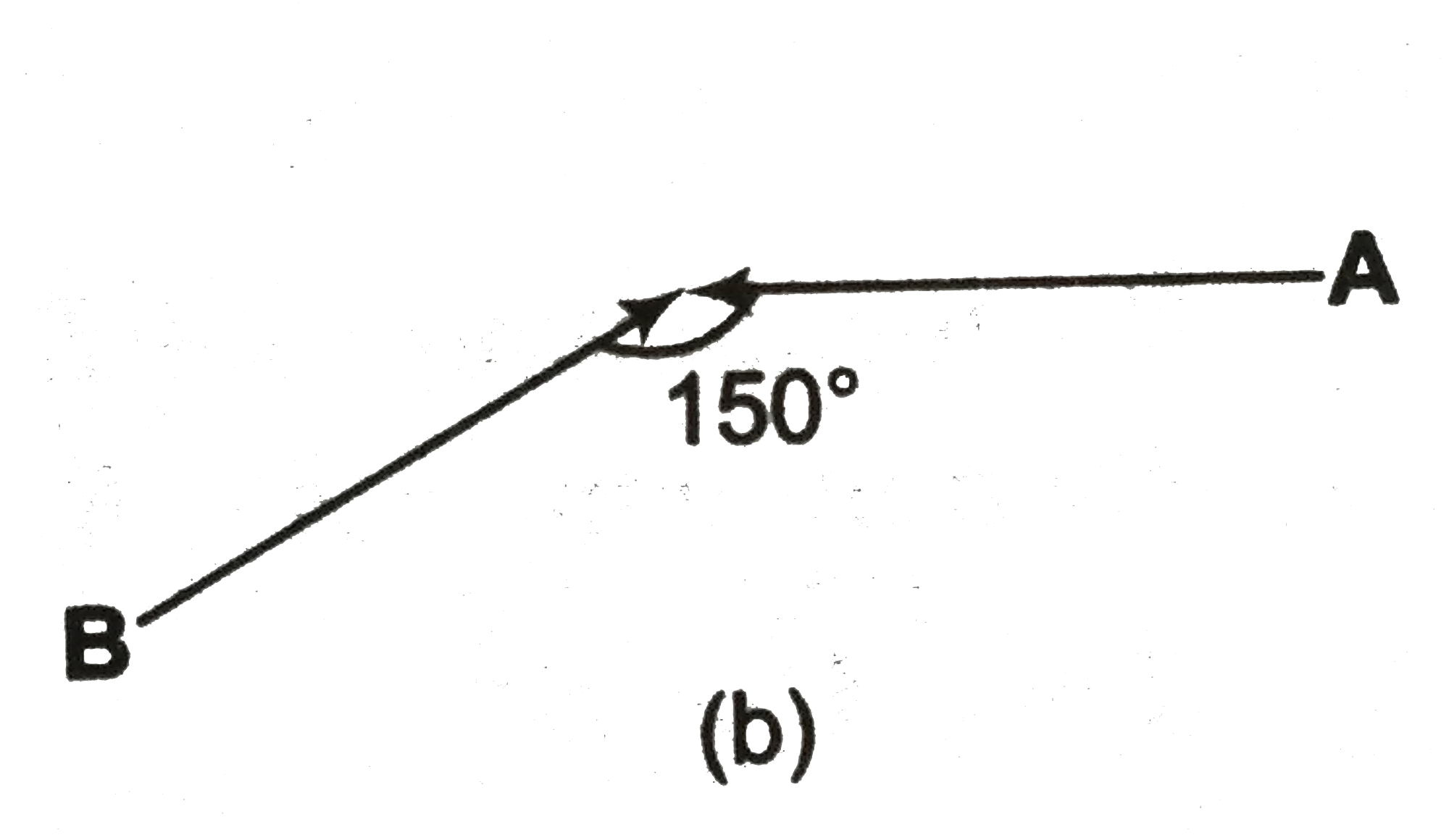
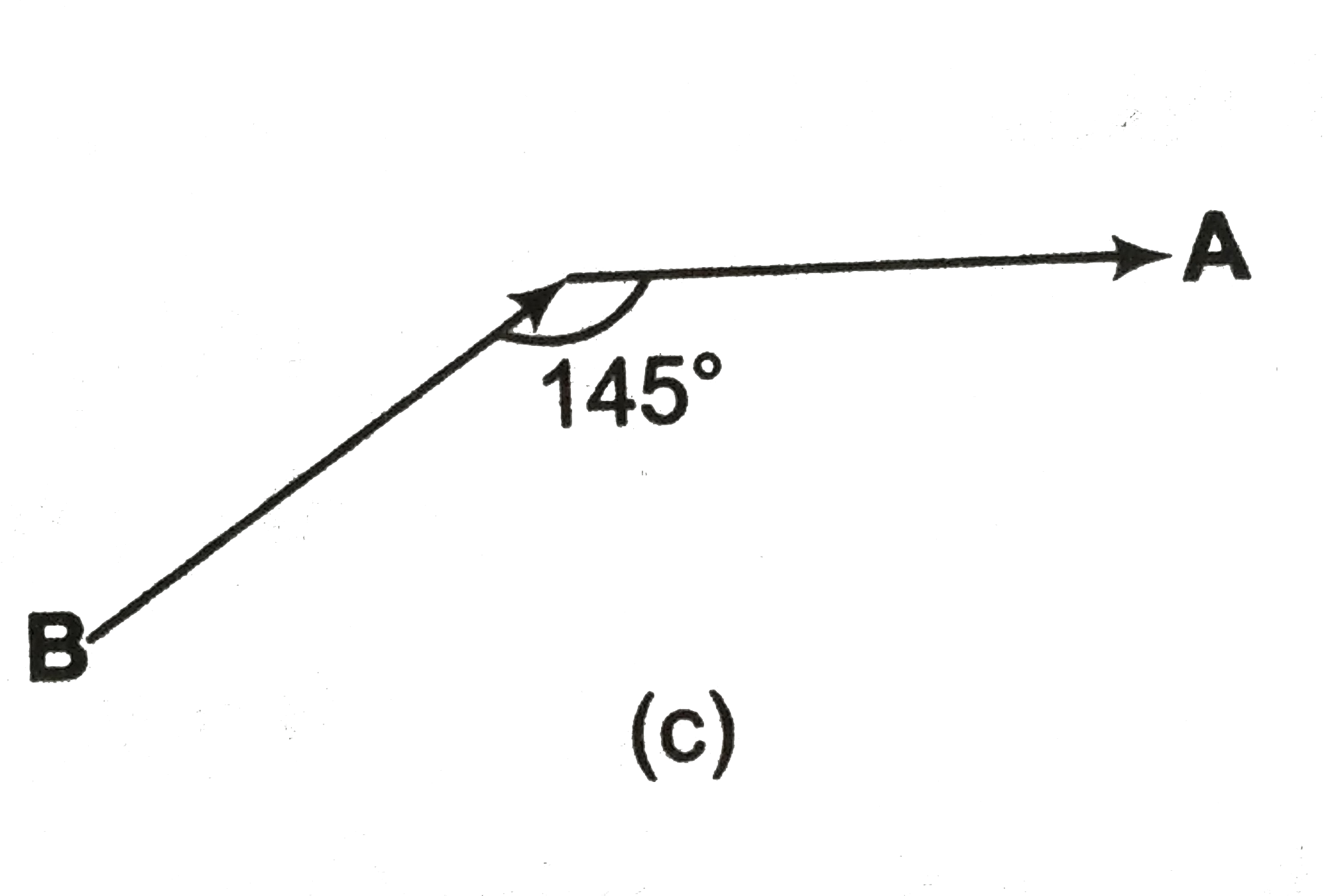 . View Solution
. View SolutionWhat is the angle between →A and →B, If →A and →B are the adjacent sides of a parallelogram drwan from a common point and the area of the parallelogram is AB/2?
View SolutionDefine →a×→b and prove that ∣∣→a×→b∣∣=(→a.→btanθ, where θ is the angle between →a and →b) .
View Solution
