A rod AB is 1m long. The temperature of its one end A is maintained at 100∘C and other end B at 10∘C, the temperature at a distance of 60 cm from point B is
64∘C
36∘C
46∘C
72∘C
The correct Answer is:A
To solve the problem of finding the temperature at a distance of 60 cm from point B on a rod AB that is 1 meter long, we can use the concept of steady-state heat conduction. Here are the steps to find the solution:
1. Understand the Setup:
- The rod AB is 1 meter long.
- Temperature at end A (0 cm) = 100°C.
- Temperature at end B (100 cm) = 10°C.
- We need to find the temperature (θ) at a point 60 cm from B (which is 40 cm from A).
2. Define the Lengths:
- Distance from B to the point where we want to find the temperature = 60 cm = 0.6 m.
- Distance from A to the point = 1 m - 0.6 m = 0.4 m.
3. Set Up the Heat Transfer Equation:
- The heat transfer rate (Q) through the rod can be expressed using Fourier's law of heat conduction:
Q=kA(T1−T2)L
- For the section from A to the point (0.4 m), we have:
Q=kA(100−θ)0.4
- For the section from the point to B (0.6 m), we have:
Q=kA(θ−10)0.6
4. Equate the Heat Transfer Rates:
- Since the heat transfer rate must be the same at steady state, we can set the two equations equal to each other:
kA(100−θ)0.4=kA(θ−10)0.6
- The kA terms cancel out:
100−θ0.4=θ−100.6
5. Cross-Multiply to Solve for θ:
- Cross-multiplying gives:
0.6(100−θ)=0.4(θ−10)
- Expanding both sides:
60−0.6θ=0.4θ−4
6. Combine Like Terms:
- Rearranging the equation:
60+4=0.6θ+0.4θ
64=θ
7. Final Result:
- The temperature at a distance of 60 cm from point B is:
θ=64°C
- The rod AB is 1 meter long.
- Temperature at end A (0 cm) = 100°C.
- Temperature at end B (100 cm) = 10°C.
- We need to find the temperature (θ) at a point 60 cm from B (which is 40 cm from A).
- Distance from B to the point where we want to find the temperature = 60 cm = 0.6 m.
- Distance from A to the point = 1 m - 0.6 m = 0.4 m.
- The heat transfer rate (Q) through the rod can be expressed using Fourier's law of heat conduction:
Q=kA(T1−T2)L
- For the section from A to the point (0.4 m), we have:
Q=kA(100−θ)0.4
- For the section from the point to B (0.6 m), we have:
Q=kA(θ−10)0.6
- Since the heat transfer rate must be the same at steady state, we can set the two equations equal to each other:
kA(100−θ)0.4=kA(θ−10)0.6
- The kA terms cancel out:
100−θ0.4=θ−100.6
- Cross-multiplying gives:
0.6(100−θ)=0.4(θ−10)
- Expanding both sides:
60−0.6θ=0.4θ−4
- Rearranging the equation:
60+4=0.6θ+0.4θ
64=θ
- The temperature at a distance of 60 cm from point B is:
θ=64°C
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY AND HEAT TRANSFERExercise:Match the columns
Explore 4 Videos
- CALORIMETRY & HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY & HEAT TRANSFERExercise:Level 2 Subjective
Explore 14 Videos
- CENTRE OF MASSBook:DC PANDEY ENGLISHChapter:CENTRE OF MASSExercise:Medical entrances gallery
Explore 27 Videos
Similar Questions
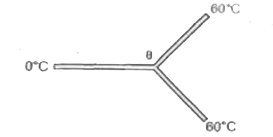
Three identical rods have been joined at a junction to make it a Y shape structure .If two free ends are maintained at 60∘C and the thired end is at 0∘C then what is the juction temperature θ?
View SolutionA rod of negligible heat capacity has a length of 50 cm, area of cross section 5cm2 and thermal conductivity 500 W/m∘C. The temperature of one end is maintained at 0∘C and that fo the other end is slowly and linearly varied from 0∘C to 60∘C in 20 min. Assuming no heat loss through the lateral side, the total heat transmitted throught he rod in 20 minutes is
View SolutionThree identical rods have been joined at a junction to make it a Y shape structure. If two free ends are maintained at 45∘C and the end is at 0∘C, then what is the junction temperature T?

View SolutionA rod of negligible heat capacity has length 20cm, area of cross section 1.0cm2 and thermal conductivity 200Wm−1C−1 . The temperature of one end is maintained at 0∘C and that of the other end is slowly and linearly varied from 0∘C to 60∘C in 10 minutes. Assuming no loss of heat through the sides, find the total heat transmitted through the rod in these 10 minutes.
View SolutionA metal rod AB of length 10x has its one end A in ice at 0∘C, and the other end B in water at 100∘C. If a point P one the rod is maintained at 400∘C, then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of evaporation of water is 540cal/g and latent heat of melting of ice is 80cal/g. If the point P is at a distance of λx from the ice end A, find the value λ. [Neglect any heat loss to the surrounding.]
View SolutionThree rods of identical cross - section and length are made of three different material of thermal conductivity k1,k2 and k3 respectively. They are joined together at their ends to make a long rod (See figure). One end of the long rod is maintained at 100∘C and the other at 0∘C ( See figure ). If the joints of the rod are at 70∘C and 20∘C in steady state and there is no loss of energy form the surface of the rod, the correct relationship between k1,k2 and k3 is
View SolutionThree rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C. Calculate the temperature of the junction B, C and D. The thermal conductivity of X is 0.92cal/sec−cm∘C and that of Y is 0.46cal/sec−cm−∘C.

View SolutionA metal rod AB of length 10x has it one end in ice at 0∘C and the other end B in water at 100∘C If a point P on the rod is maintained at 400∘C then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of melting of ice is 80cal/g If the point P is at a distance of λx from the ice end A find the value of λ [neglect any heat loss to the surrounding] .
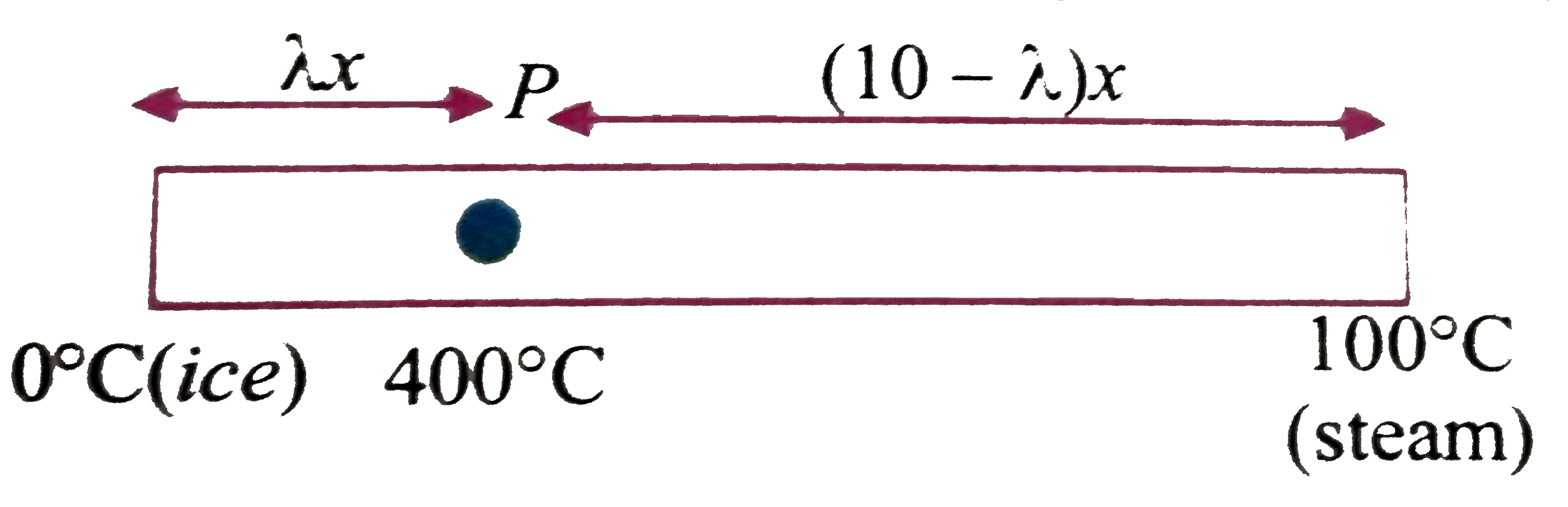 .
.
View SolutionIn a steady state of thermal conduction, temperature of the ends A and B of a 20 cm long rod are 100∘C and 0∘C respectively. What will be the temperature of the rod at a point at a distance of 9 cm from the end A of the rod
View SolutionOne end of conducting rod is maintained at temperature 50∘C and at the other end ice is melting at 0∘C. The rate of melting of ice is doubled if:
View Solution

