In MKS system, Stefan's constant is denoted by σ. In CGS system multiplying factor of σ will be
1
103
105
102
The correct Answer is:B
To find the multiplying factor of Stefan's constant (σ) when converting from the MKS (Meter-Kilogram-Second) system to the CGS (Centimeter-Gram-Second) system, we can follow these steps:
Step 1: Identify the units of Stefan's constant in the MKS system.
In the MKS system, Stefan's constant (σ) is expressed in the units of:
Joulesm−2s−1K−4
Step 2: Convert the units from MKS to CGS.
We need to convert each component of the units from MKS to CGS:
- Joules (J): In CGS, 1 Joule = 107 ergs.
- Meters (m): In CGS, 1 meter = 102 centimeters.
- Seconds (s): The unit of time remains the same in both systems.
- Kelvin (K): The unit of temperature also remains the same in both systems.
Step 3: Substitute the conversions into the unit of σ.
Now we can substitute the conversions into the unit of σ:
σ=Joulesm2⋅s⋅K4=107ergs(102cm)2⋅s⋅K4
Step 4: Simplify the expression.
Now we simplify the expression:
σ=107ergs104cm2⋅s⋅K4=107104⋅ergscm2⋅s⋅K4
σ=107−4⋅ergscm2⋅s⋅K4=103⋅ergscm2⋅s⋅K4
Step 5: Determine the multiplying factor.
From the simplification, we find that the multiplying factor when converting σ from MKS to CGS is:
103
Conclusion
Thus, the multiplying factor of σ in the CGS system is 103.
---
In the MKS system, Stefan's constant (σ) is expressed in the units of:
Joulesm−2s−1K−4
We need to convert each component of the units from MKS to CGS:
- Joules (J): In CGS, 1 Joule = 107 ergs.
- Meters (m): In CGS, 1 meter = 102 centimeters.
- Seconds (s): The unit of time remains the same in both systems.
- Kelvin (K): The unit of temperature also remains the same in both systems.
Now we can substitute the conversions into the unit of σ:
σ=Joulesm2⋅s⋅K4=107ergs(102cm)2⋅s⋅K4
Now we simplify the expression:
σ=107ergs104cm2⋅s⋅K4=107104⋅ergscm2⋅s⋅K4
σ=107−4⋅ergscm2⋅s⋅K4=103⋅ergscm2⋅s⋅K4
From the simplification, we find that the multiplying factor when converting σ from MKS to CGS is:
103
Thus, the multiplying factor of σ in the CGS system is 103.
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Taking it together
51 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Assertion and reason
17 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check points 16.3
20 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
Knowledge Check
MKS system is similar to
ACGS systemBFPS systemCSI systemDNone of these
Dimensional formula for stefan’s constant is: (here K denotes the temperature)
View SolutionConvert gravitational constant (G) from CGS to MKS system.
View SolutionConsider the following two statements:
A. Kinear momentum of the system remains constant.
B. Centre of mass of the system remains at rest
View Solution(k−1)x+13y=4
k(x+2y)=7
In the system of linear equations above, k is a constant. If the system has no system, what is the value of k?
View SolutionThe radiation emitted per unit time by unit area of a black body at temperature T is σT4 wehre σ is the Stefan-Boltzmann constant. The constant σ can also be expressed in terms of Boltmann's constant (k), Planck's constant (h) and speed of light (3) as σ=Akαhβcγ where A,α,β and γ are dimensionless constants. The set (α,β,γ) is givne by
View SolutionFind equivalent spring constant for the system:
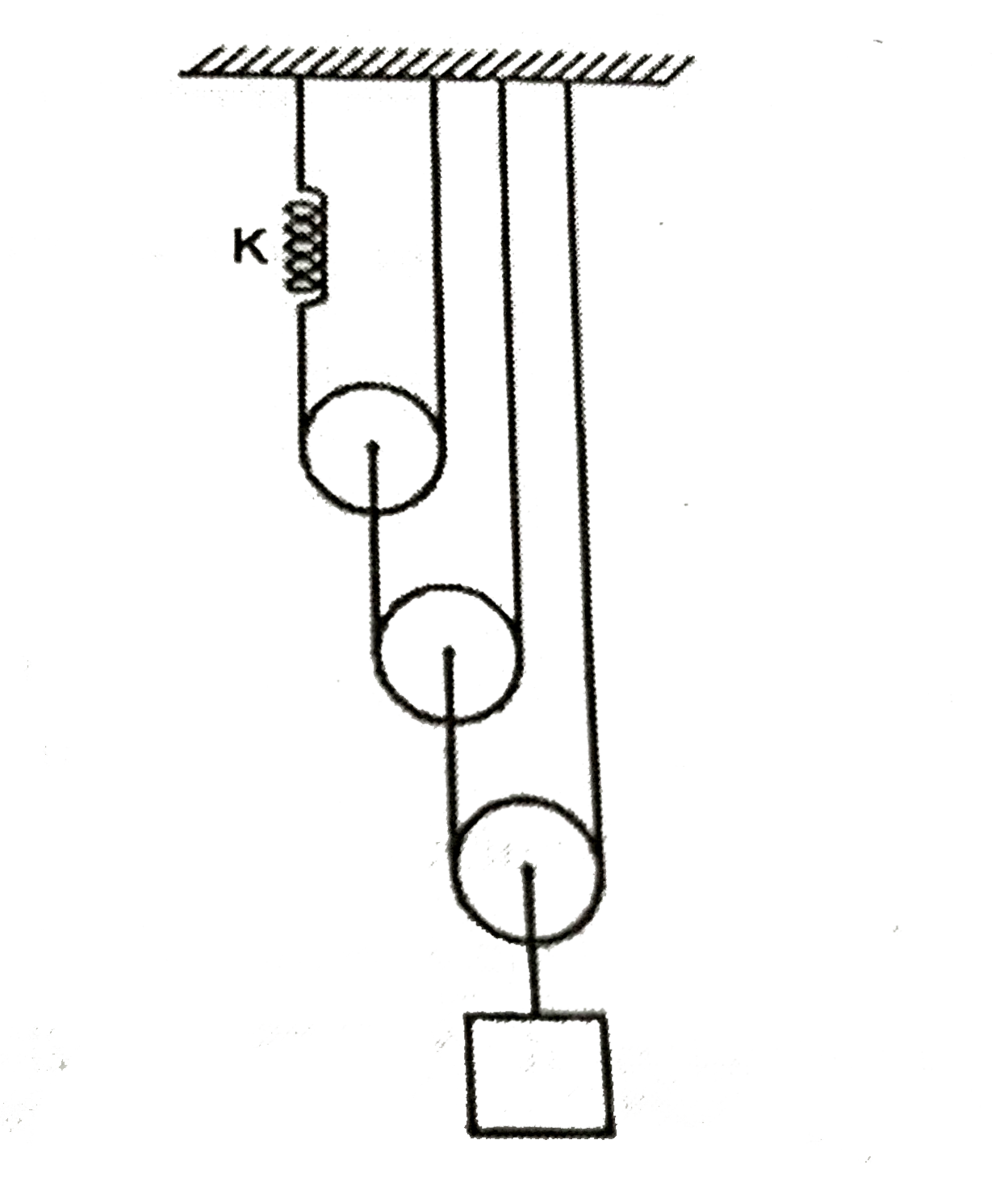
View SolutionConsider the following two statements:
A. linear momentum of the system remains constant.
B. Centre of mass of the system remains at rest
View Solution
