Question

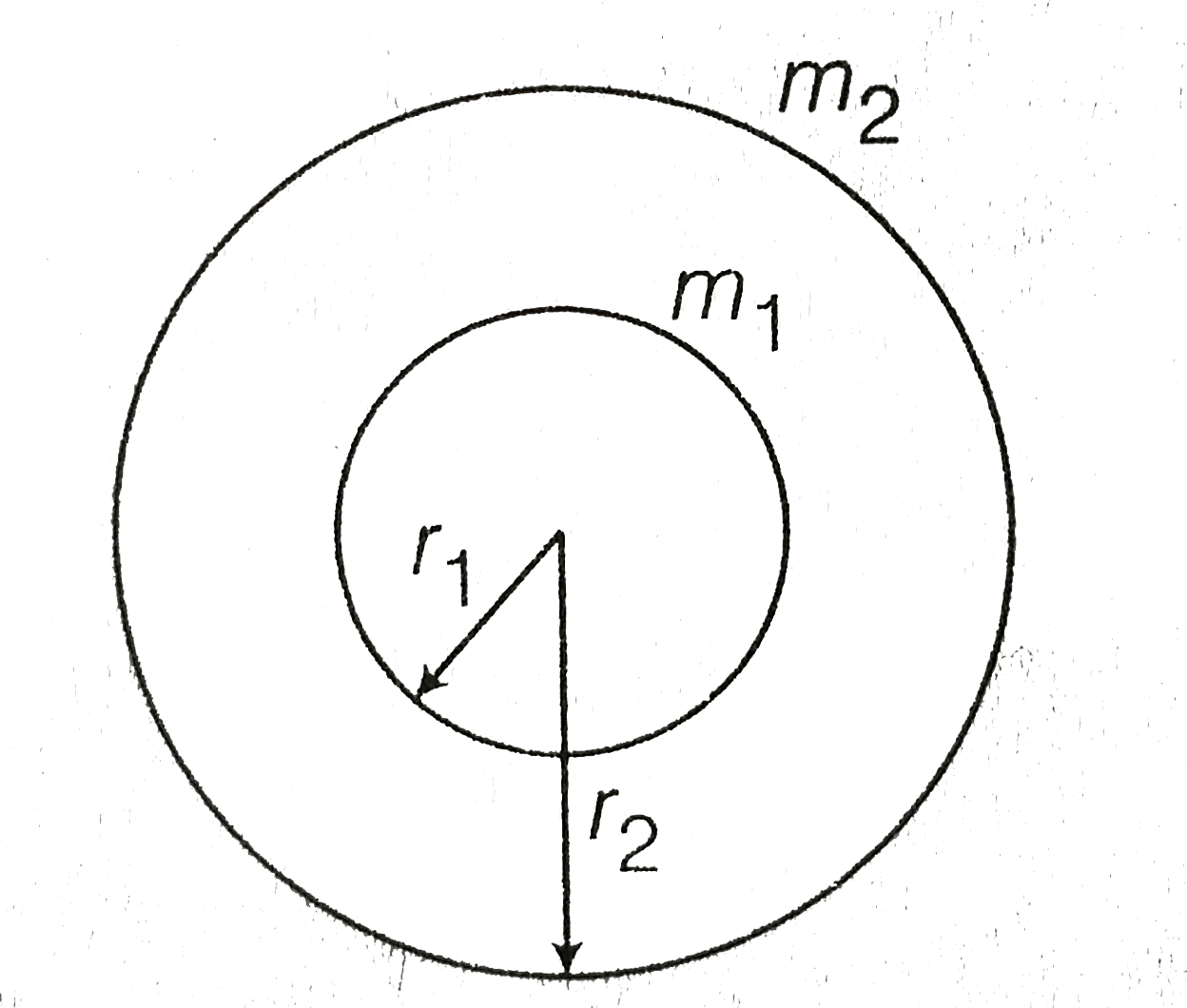
Two concentric spherical shells have masses $m_1\text{and}{m}_2$ and radii $r_1\text{and}{r}_2(r_2>r_1)$. What is the force exerted by this system on a particle of mass $m_3$. If it is placed at a distance $r(r_1<r<r_2)$ from the centre ?

Explanation

To solve the problem, we need to determine the gravitational force exerted by two concentric spherical shells on a particle of mass $$m_3$$ placed at a distance $$r$$ from the center, where $$r_1<r<r_2$$.

1. Understanding the Setup:
We have two spherical shells:
- Inner shell with mass \( m_1 \) and radius \( r_1 \).
- Outer shell with mass \( m_2 \) and radius \( r_2 \).
The particle of mass \( m_3 \) is located at a distance \( r \) from the center, where \( r_1 < r < r_2 \).

2. Applying Shell Theorem:
According to the shell theorem, the gravitational field inside a spherical shell (at a distance less than its radius) is zero. Therefore, the gravitational field due to the outer shell (mass \( m_2 \)) at the position of the particle \( m_3 \) is also zero because \( m_3 \) is located inside the outer shell.

3. Calculating the Gravitational Field from the Inner Shell:
The gravitational field \( E \) due to the inner shell (mass \( m_1 \)) at the position of the particle \( m_3 \) is given by the formula:
\( E = \frac{G m_1}{r^2} \)
where \( G \) is the universal gravitational constant.

4. Calculating the Gravitational Force on \( m_3 \):
The gravitational force \( F \) acting on the particle \( m_3 \) due to the inner shell is given by:
\( F = m_3 \cdot E \)
Substituting the expression for \( E \):
\( F = m_3 \cdot \frac{G m_1}{r^2} \)
Thus, the force exerted by the system on the particle \( m_3 \) is:
\( F = \frac{G m_1 m_3}{r^2} \)

5. Direction of the Force:
The gravitational force \( F \) is directed towards the center of the spherical shells.

Final Answer:
The force exerted by the system on the particle of mass \( m_3 \) is:
\( F = \frac{G m_1 m_3}{r^2} \)
and it is directed towards the center of the shells.

---