A particle is moving uniformly in a circular path of radius r. When it moves through an angular displacement $θ$ , then the magnitude of the corresponding linear displacement will be

A

2 r cos $(\frac{θ}{2})$

B

2 r cot $(\frac{θ}{2})$

C

2 r tan $(\frac{θ}{2})$

D

2 r sin $(\frac{θ}{2})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

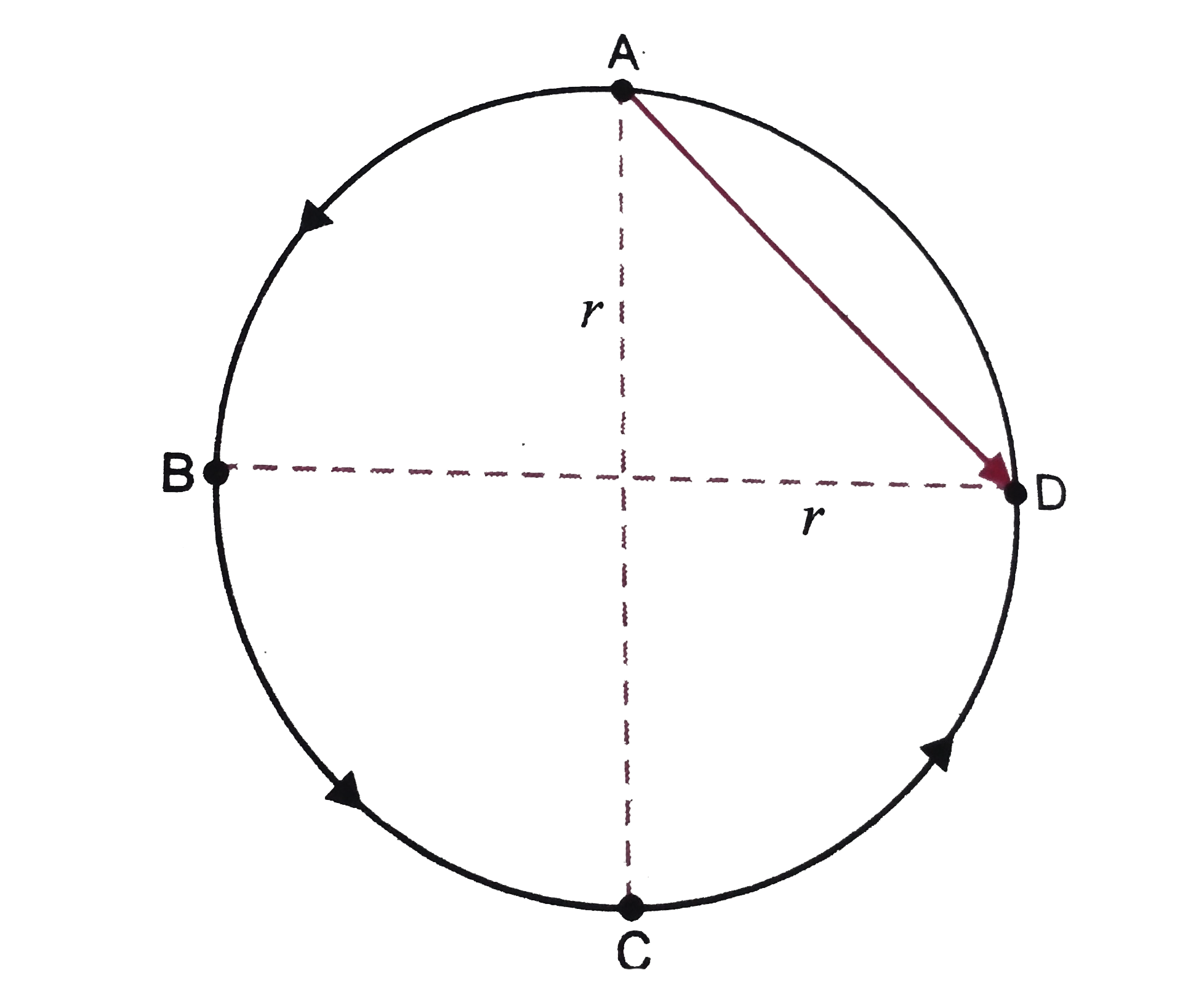
The figure is shown as below

$ln Δ A O B, \frac{sin (θ)}{2} = \frac{A B}{A O} (∵ A O = r)$
$A B = A O sin . \frac{θ}{2} \Rightarrow A B = r sin . \frac{θ}{2}$
$A C = A B + B C (∵ A B = B C)$
$r = \frac{r sin θ}{2} + r sin . \frac{θ}{2}, A c = r sin . \frac{θ}{2} + r sin . \frac{θ}{2}$
$A C = 2 r sin . \frac{θ}{2}$
So, the magnitude of the corresponding linear displacement will be $2 r sin . \frac{θ}{2}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS CIRCULAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle is moving on a circular path of radius r with uniform speed v. What is the displacement of the particle after it has described an angle of $60^{\circ}$ ?
A $r \sqrt{2}$
B $r \sqrt{3}$
Cr
D2r
Question 2 - Select One
A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B

AAverage speed is v/2
BThe magnitude of average velocity is v/ $π$
CThe magnitude of average acceleration is $\frac{2 v^{2}}{π R}$
DAverage velocity is zero.

DC PANDEY ENGLISH-CIRCULAR MOTION-Medical entrances s gallery

Home
Ask Doubt
Profile