An aeroplane is flying at a constant height of 1960 m with speed 600kmh−1 above the ground towards point directly over a person struggling in flood water. At what angle of sight with the vertical should be pilot release a survival kit if it is to reach the person in water ? (g=9.8ms−2)
45∘
30∘
60∘
90∘
The correct Answer is:C
To solve the problem of determining the angle at which the pilot should release a survival kit from an airplane flying at a height of 1960 m, we can follow these steps:
Step 1: Convert the speed of the airplane from km/h to m/s
The speed of the airplane is given as 600 km/h. To convert this to meters per second (m/s), we use the conversion factor 518.
Speed in m/s=600×518=300018=5003 m/s
Step 2: Calculate the time taken for the survival kit to reach the ground
The time T taken for the survival kit to fall from the height h can be calculated using the formula for free fall:
T=√2hg
Where:
- h=1960 m (height of the airplane)
- g=9.8 m/s² (acceleration due to gravity)
Substituting the values:
T=√2×19609.8=√39209.8≈√400=20 seconds
Step 3: Calculate the horizontal distance (range) the survival kit travels
The horizontal distance R that the survival kit travels while it falls can be calculated using the formula:
R=speed×T
Substituting the values:
R=(5003)×20=100003 meters
Step 4: Determine the angle of sight with the vertical
The angle θ can be found using the tangent function, where:
tan(θ)=oppositeadjacent=Rh
Substituting the values:
tan(θ)=1000031960
Calculating this gives:
tan(θ)=100003×1960≈100005880≈1.70
Step 5: Calculate the angle θ
Now we can find θ using the inverse tangent function:
θ=tan−1(1.70)
Using a calculator, we find:
θ≈60∘
Conclusion
Thus, the pilot should release the survival kit at an angle of approximately 60 degrees with respect to the vertical.
---
The speed of the airplane is given as 600 km/h. To convert this to meters per second (m/s), we use the conversion factor 518.
The time T taken for the survival kit to fall from the height h can be calculated using the formula for free fall:
- h=1960 m (height of the airplane)
- g=9.8 m/s² (acceleration due to gravity)
The horizontal distance R that the survival kit travels while it falls can be calculated using the formula:
The angle θ can be found using the tangent function, where:
Now we can find θ using the inverse tangent function:
Thus, the pilot should release the survival kit at an angle of approximately 60 degrees with respect to the vertical.
Topper's Solved these Questions
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:A. Taking it together
Explore 1 Video
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:Taking it together
Explore 96 Videos
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:Check Point 4.2
Explore 20 Videos
- MEASUREMENT AND ERRORSBook:DC PANDEY ENGLISHChapter:MEASUREMENT AND ERRORSExercise:Subjective
Explore 19 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:(C )Medical entrances gallery
Explore 32 Videos
Similar Questions
A jet aeroplane is flying at a constant height of 2 km with a speed 360kmh−1 above the ground towards a target and releases a bomb. After how much time it will hit the target and what will be the horizontal distance of the aeroplane from the target so that the bomb should hit the target ? (Take g=10ms−2)
View SolutionAn aeroplane is flying vertically upwards. When it is at a height of 1000m above the ground and moving at a speed of 367m/s., a shot is fired at it with a speed of 567 ms−1 from a point directly below it. What should be the acceleration of aeroplane so that it may escape from being hit?
View Solution
Knowledge Check
A fighter plane flying horizontally at an altitude of 1.5km with speed 720kmh−1 passes directly over head an anticraft gun.
At what angle from the vertical should the gun be fired from the shell with muzzle speed 600ms−1 to hit plane.
At what minimum altitude should the pilot fly the plane to avoid being hit ? ( Take g= 10 ms−2).Asin−1(13) , 16kmBsin−1(23) ,16 kmCcos−1(13) 16mDcos−1(23) ,16mAn aeroplane flying horizontally with a speed of 360 km h−1 releases a bomb at a height of 490 m from the ground. If g = 9. 8 m s−2 , it will strike the ground at
A10 kmB100 kmC1 kmD16 km
A fighter plane flying horizontally at an altitude of 1.5 km with speed 720 km h−1 passes diretly overhead an anti-aircraft gun. At what angle from the vertical should the gun he fired for the shell with muzzle speed 600 m s−1 to hit the plane. (Take g = 10 m s−1)
View SolutionAn enemy plane is flying horizontally at an altitude of 2 km with a speed of 300ms−1 An army man with an anti-aircraft gun on the ground sights hit enemy plane when it is directly overhead and fires a shell with a muzzle speed of 600ms−1. At what angle with the vertical should the gun be fired so as to hit the plane ?
View SolutionA fighter plane is flying horizontally at an altitude of 1.5 km with speed 720kmh−1. At what angle of sight (w.r.t horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target? (Takeg=10ms−2)
View SolutionAn aeroplane is flyind horizontally at a height of 2 km and with a velocity of 720 km/h. A bag containing ration is to be dropped to the Jawans on the ground then find out
(i) How far from the Jawans should the bag be released so that it falls directly over them
(ii) Time taken by bag to reach the ground
(iii) Velocity of bag when it reach the ground.
(iv) At which angle the bag will reaches the ground.
(v) What path of bag will be appeared to pilot
(vi) What path of bag will be appeared to Jawans.
(vii) Position of aeroplane when bag reaches to the Jawans.(g=10m/s2)
View SolutionAn aeroplane is travelling at a height of 2000 m from the ground. The aeroplane, when at a point P, drops a bomb to hit a stationary target Q on the ground. In order that the bomb hits the target, what angle θ must the line PQ make with the vertical? [g=10ms−2]
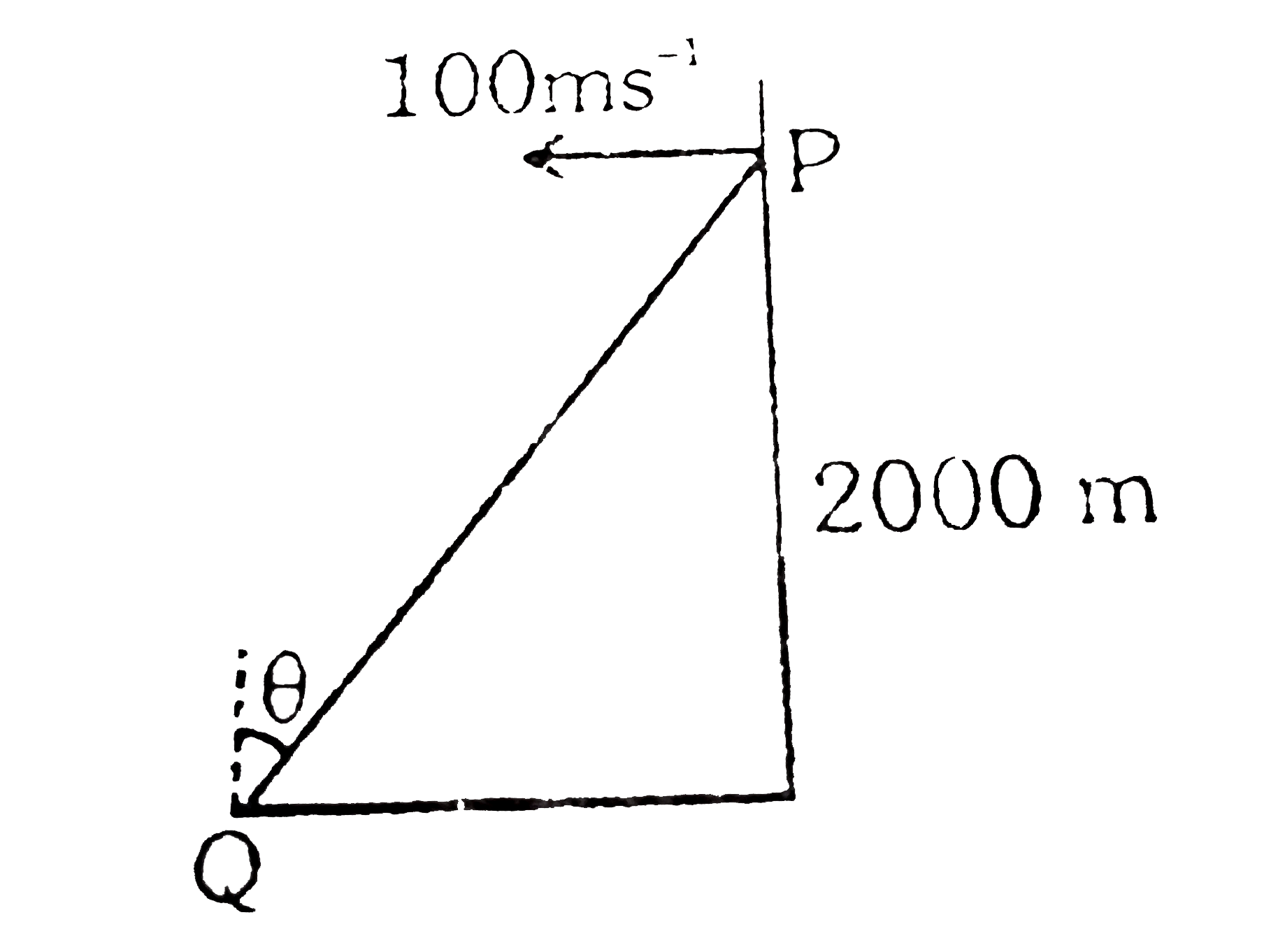
View SolutionAn aeroplane is going towrds east at a speed of 510kmh−1 at a height of2000 m. At a certain instant, the sound o theh plane heard by a ground obserger appears to come from a point vertically above him. Where is the plane at this instant? Speed of sound in air =340ms−1
View Solution