A glass wind screen whose inclination with the vertical can be changed is mounted on a car. The moves horizontally with a speed of 2m/s. At what angle α with the vertical should the wind screen placed so that the rain drops falling vertically downwards with velcoity 6m/s strike the wind screen perpendicularly?
tan−1(1/3)
tan−1(3)
cos−1(3)
sin−1(1/3)
The correct Answer is:B
To solve the problem, we need to determine the angle α at which the windscreen should be inclined so that the raindrops, falling vertically downward with a velocity of 6m/s, strike the windscreen perpendicularly while the car is moving horizontally at a speed of 2m/s.
1. Understand the Problem:
- The rain is falling vertically with a velocity Vr=6m/s.
- The car is moving horizontally with a velocity Vc=2m/s.
- We need to find the angle α such that the relative velocity of the rain with respect to the car strikes the windscreen perpendicularly.
2. Relative Velocity:
- The relative velocity of the rain with respect to the car can be expressed as:
Vr (relative)=Vr−Vc
- Here, Vr is the vertical component (downward) and Vc is the horizontal component (to the right).
3. Components of Relative Velocity:
- The vertical component of the relative velocity is Vr=6m/s (downward).
- The horizontal component of the relative velocity is Vc=2m/s (to the right).
4. Finding the Angle:
- The angle α can be found using the tangent function:
tanα=Vertical ComponentHorizontal Component=VrVc
- Substituting the values:
tanα=62=3
5. Calculating the Angle:
- To find α, we take the inverse tangent:
α=tan−1(3)
6. Final Answer:
- The angle α with the vertical at which the windscreen should be placed is:
α=tan−1(3)
- The rain is falling vertically with a velocity Vr=6m/s.
- The car is moving horizontally with a velocity Vc=2m/s.
- We need to find the angle α such that the relative velocity of the rain with respect to the car strikes the windscreen perpendicularly.
- The relative velocity of the rain with respect to the car can be expressed as:
Vr (relative)=Vr−Vc
- Here, Vr is the vertical component (downward) and Vc is the horizontal component (to the right).
- The vertical component of the relative velocity is Vr=6m/s (downward).
- The horizontal component of the relative velocity is Vc=2m/s (to the right).
- The angle α can be found using the tangent function:
tanα=Vertical ComponentHorizontal Component=VrVc
- Substituting the values:
tanα=62=3
- To find α, we take the inverse tangent:
α=tan−1(3)
- The angle α with the vertical at which the windscreen should be placed is:
α=tan−1(3)
Topper's Solved these Questions
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:MCQ_TYPE
Explore 27 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:COMPREHENSION_TYPE
Explore 19 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 10 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Medical entrances gallery
Explore 39 Videos
Similar Questions
A glass wind screen whose inclination with the vertical can be changed in mounted on a car. The car moves horizontal with a speed of 2m/s. At what angle α with the vertical should the wind screen be placed so that the rain drops falling vertically downwards with velocity 6m/s strike the wind screen -perpendicularly?
View SolutionA boy is running on a horizontal road with a velocity of 5 m/s. At what angle should he hold his umbrella in order to protect him self from the rain if the rain is falling vertically with a velocity of 10 m/s?
View SolutionA man is travelling at 10.8 kmph in a topless car on a rainy day. He holds an umbrella at an angle of 37° with the vertical so that he does not wet. If rain drops falls vertically downwards, what is the rain velocity ?
View SolutionA man is travelling at 10.8 kmph in a topless car on a rainy day. He holds an umbrella at an angle of 37∘ with the vertical so that he does not wet. If rain drops falls vertically downwards, what is the rain velocity ?
View SolutionA car is moving on horizontal ground with a velocity vm s−1 with respect to earth. The driver of the car observes the rain to be falling vertically downwards with velocity 2vm s−1 . What is the velocity of the rain with respect to the ground ?
View SolutionWind is blowing in the north direction at speed of 2 m/s which causes the rain to fall at some angle with the vertical. With what velocity should acyclist drive so that the rain appears vertical to him:
View SolutionA person walking at 4 m/s finds rain drops falling slantwise into his face with a speed of 4 m/s at an angle of 30∘ with the vertical . Show that the actual speed of the rain drops is 4 m/s .
View SolutionA man is running up an inclined plane ( making an angle θ with the horizontal ) with a speed u. Rain drops falling at an angle α with the vertical appear to the man as if they are falling at an angle of 45∘ with the horizontal . The speed of the rain drops is
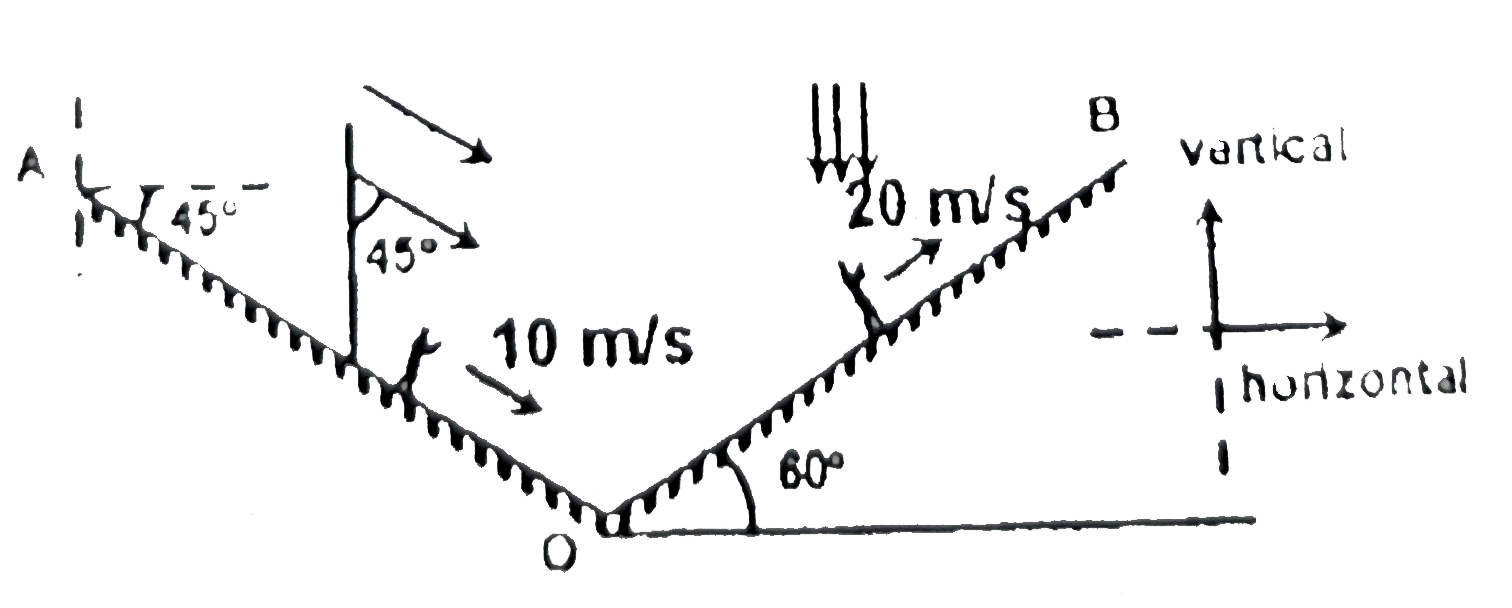
View SolutionThere are two incline planes AO and OB inclined at 45∘ and 60∘ respectively with the horizontal as shown in the figure. When a man moves on the inclined plane AO he is oberves that the rain drops are falling 45∘ with the vertical. When the man moves on the inclined plane OB, he observes that the raindrops are falling vertically downward with the horizontal. Then actual speed of rain is
View SolutionRain drops fall vertically at a speed of 20m/s. At what angle do they fall on the wind screen of a car moving with a velocity of 15m/, if the wind screen velocity incined at an agle of 23∘ to the vertical (cot−143≈37∘)
View Solution

