find kinetic energy, electrostatic potential energy and total
. energy of single electron in 2nd excited state of Li+2 atom.
The correct Answer is:A, B, C
To find the kinetic energy, electrostatic potential energy, and total energy of a single electron in the second excited state of the Li+2 atom, we can follow these steps:
Step 1: Identify the quantum numbers
The second excited state corresponds to the principal quantum number n=3. For lithium, the atomic number Z=3.
Step 2: Calculate the total energy
The formula for the energy of an electron in a hydrogen-like atom is given by:
E=−13.6Z2n2
Substituting the values for lithium:
E=−13.6×3232
Calculating this gives:
E=−13.6×99=−13.6 eV
Step 3: Calculate the kinetic energy
The kinetic energy K of the electron in a hydrogen-like atom is equal to the absolute value of the total energy:
K=|E|=13.6 eV
Step 4: Calculate the electrostatic potential energy
The electrostatic potential energy U is given by:
U=2E
Substituting the value of E:
U=2×(−13.6)=−27.2 eV
Step 5: Calculate the total energy
The total energy Etotal is simply the sum of kinetic energy and potential energy:
Etotal=K+U
Substituting the values:
Etotal=13.6+(−27.2)=−13.6 eV
Summary of Results
- Kinetic Energy K=13.6 eV
- Electrostatic Potential Energy U=−27.2 eV
- Total Energy Etotal=−13.6 eV
The second excited state corresponds to the principal quantum number n=3. For lithium, the atomic number Z=3.
The formula for the energy of an electron in a hydrogen-like atom is given by:
The kinetic energy K of the electron in a hydrogen-like atom is equal to the absolute value of the total energy:
The electrostatic potential energy U is given by:
The total energy Etotal is simply the sum of kinetic energy and potential energy:
- Kinetic Energy K=13.6 eV
- Electrostatic Potential Energy U=−27.2 eV
- Total Energy Etotal=−13.6 eV
Topper's Solved these Questions
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Example Type 1
2 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Example Type 2
6 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MODERN PHYSICS - 2BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Subjective
10 Videos
Similar Questions
Ratio between potential energy, kinetic energy and total energy of electron in hydrogen atom are
View SolutionFind the electrostatic potential energy of the system shown in the figure
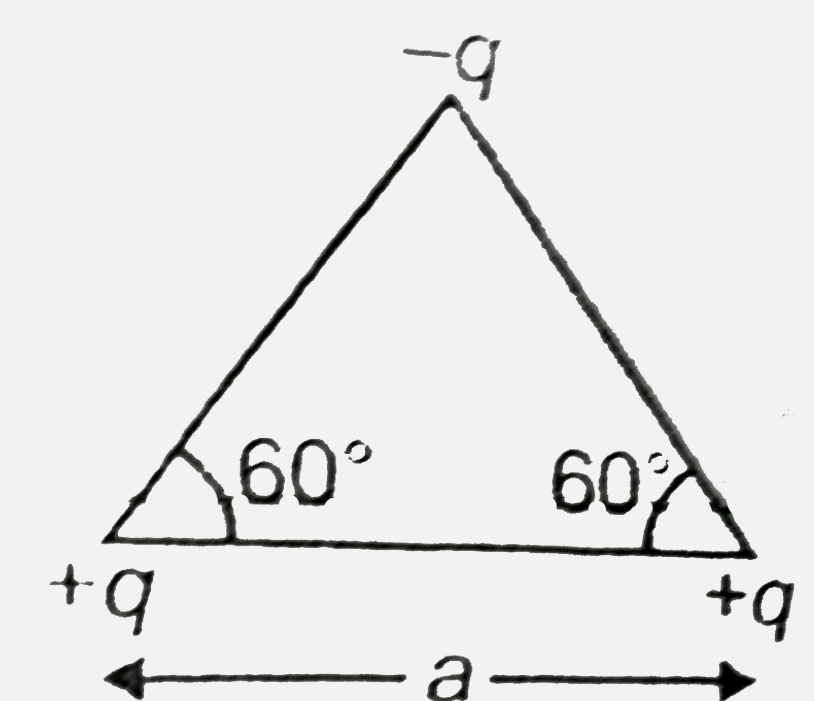
View SolutionThe total energy of an electron in He+ ion in 2 nd orbit is −xJ.If the KE of an electron in 2nd excited state of Li2+ ion is (a.x) J ,find a.
View SolutionCalculate the energy of Li+2 atom for 2nd excited state.
View SolutionThe ratio of kinetic energy to the total energy of an electron in a Bohr orbit of the hydrogen atom, is
View SolutionThe ratio of kinetic energy to the total energy of an electron in a Bohr orbit of the hydrogen atom, is
View SolutionIn the Bohr's orbit, what is the ratio of total kinetic energy and total energy of the electron
View SolutionThe total energy of an electron in the first excited state of hydrogen atom is -3.4 eV.
(a) What is kinetic energy of electron in this state?
(ii) What is potential energy of electron in this state?
(c) Which of the answers above would change if the choice of zero of potential energy is changed?
View SolutionFind the kinetic energy, potential energy and total energy in
first and second orbit of hydrogen atom if potential energy in first orbit is taken
to be zero.
View SolutionFind the kinetic energy, potential energy and total energy in
first and second orbit of hydrogen atom if potential energy in first orbit is taken
to be zero.
View Solution
