Question

A gas of hydrogen - like atoms can absorb radiations of $698eV$. Consequently , the atoms emit radiation of only three different wavelengths . All the wavelengthsare equal to or smaller than that of the absorbed photon.
a Determine the initial state of the gas atoms.
b Identify the gas atoms
c Find the minimum wavelength of the emitted radiation ,
d Find the ionization energy and the respective wavelength for the gas atoms.

Answer

B::C::D

Explanation

(a) `(n(n-1)/(2) = 3`
`:. N =3
i.e after excitation atom jumps to second
excited state. Hence, `n_f = 3`. So `n_1` can be 1 or 2.
if n_i = 1` than the energy absorbed, Hence, the
emitted wavelength is either equal to or greater
than the absorbed wavelength, Hence, `n_1 !=1.`

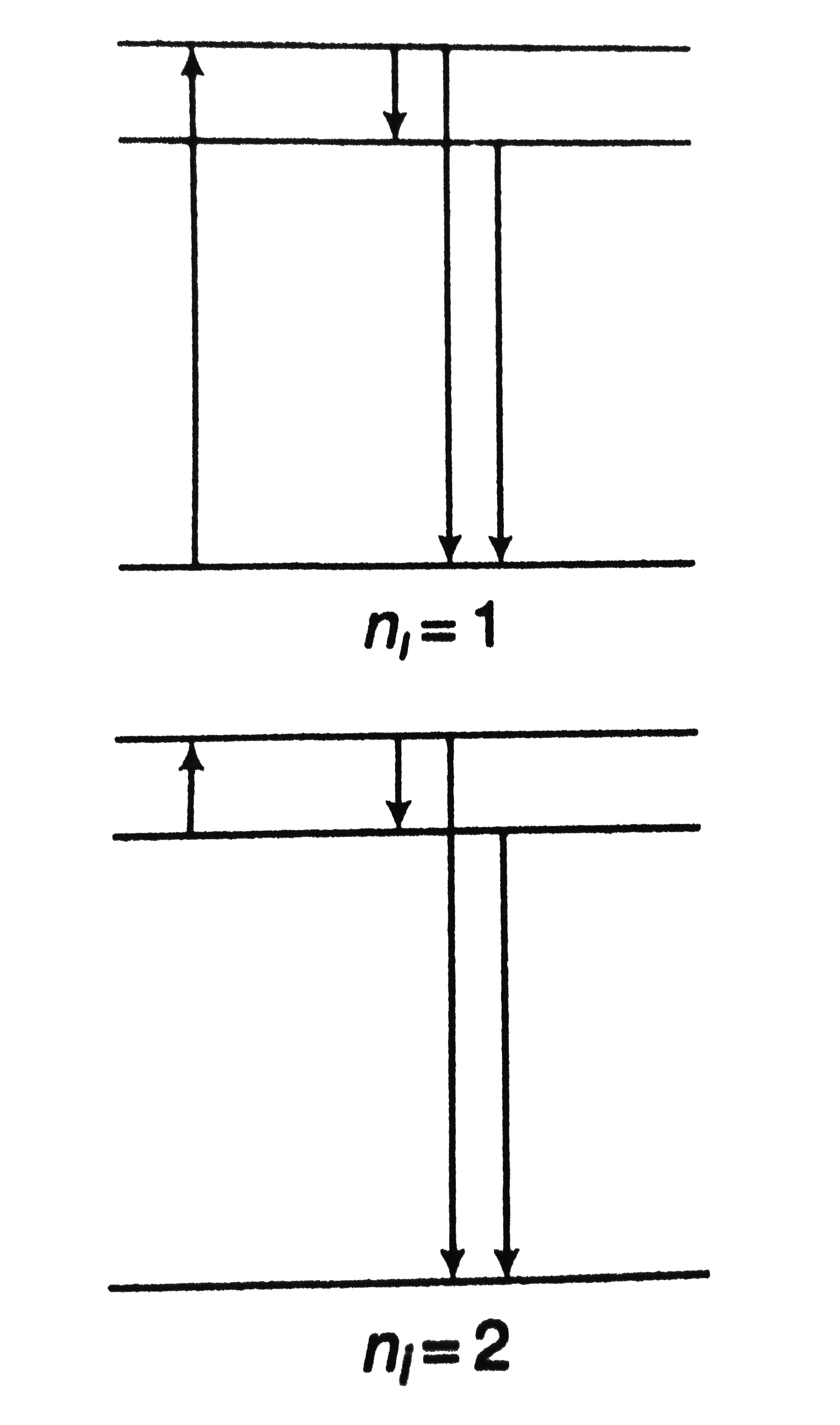
`if n_i =2, then E_e ge E_(alpha).`
Hence `lambda_e le lambda_b`
(b) `E_3 - E_2 = 68 eV`
`:. (13.6)(Z^2) ((1)/(4) - (1)/(9) = 68`
Z= 6
(c ) `lambda_(min) = (12375)/(E_3 - E_1)`
`=(12375)/((13.6)(6)^2((1-(1)/(9))) = 28.43 Å`
(d) `ionization energy = (13.6)(6)^2 = 489.6 eV`
`lambda = (12375)/(489.6) = 25.3 Å`