Light of wavelengthλ=500nm falls on two narrow slits placed a distance d = 50×10−4 cm
apart, at an angle ϕ=30∘ relative to the slits as shown in figure. On the lower slit a transparent slab of thickness 0.1 mm and refractive index 32 is placed. The interference pattern is observed at a distance D=2m from the slits. Then, calculate
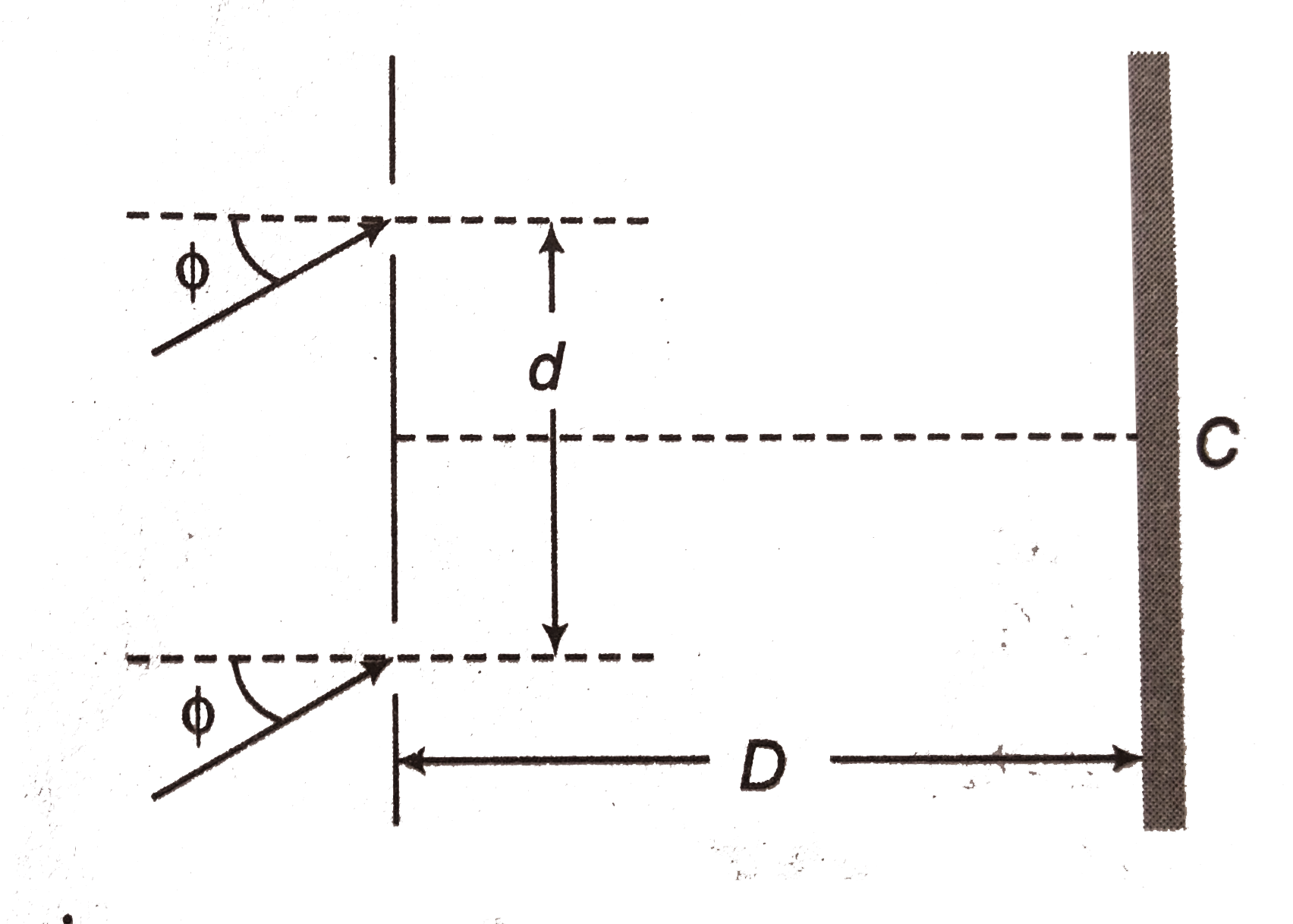
(a) position of the central maxima.
(b) the order of maxima at point C of screen .
(c)how many fringes will pass C, if we remove the transparent slab from the lower slit?
(a) dsinϕ=Δx1
=(50×10−4)sin30∘
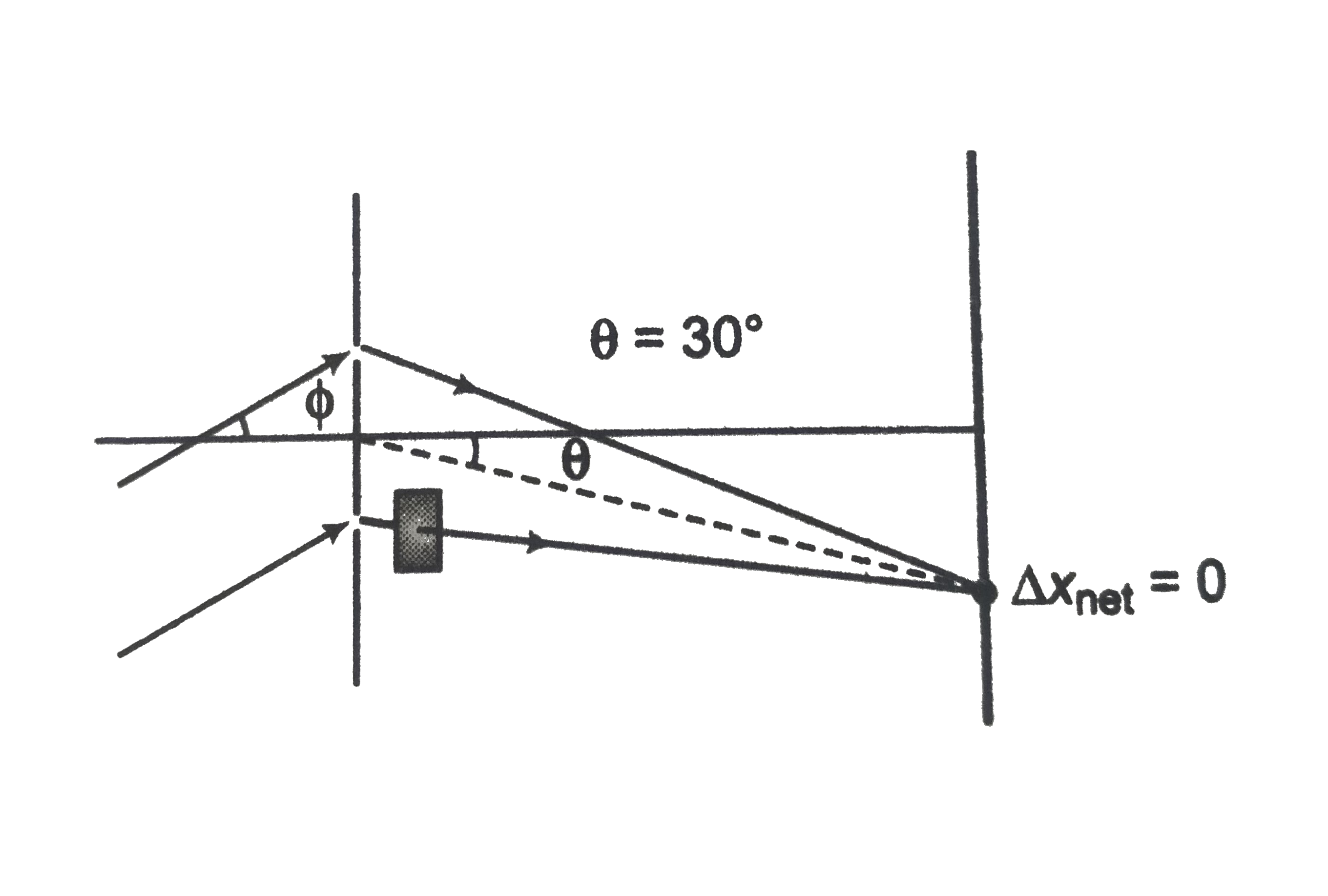
=2.5×10−3 cm
Δx2=(μ−1)t
=(32−1)(0.01)
=5.0×10−3cm
Δx2−Δx1=2.5×10−3cm=Δx1 (also)
∴ Central maxima will be obtained at θ=30∘ below C.
(b) At CΔXnet=2.5×10−3cm=nλ
∴n=2.5×10−3λ
=2.5×10−3500×10−7
=50
(c) Number of fringes that will pass if we remove the slab
=Path difference due to slabλ
5×10−3500×10−7
= 100.
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Comprehensionn Based
4 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
Two slits in YDSE are placed 1 mm from each other. Interference pattern is observed on a screen placed 1m from the plane of slits. What is the angular fringe width for a light of wavelength 400 nm
View SolutionTwo slits in YDSE are placed 2 millimeter from each other. Interference pattern is observed on a screen placed 2 m from the plane of slits. What is the fringe width for a light of wavelength 400 nm?
View Solution
Knowledge Check
In a Young's double slit experiment, (slit distance d) monochromatic light of wavelength λ is used and the fringe pattern observed at a distance D from the slits. The angular position of the bright fringes are
Asin−1(Nλd)Bsin−1⎛⎜ ⎜⎝(N+12)λd⎞⎟ ⎟⎠Csin−1(NλD)Dsin−1⎛⎜ ⎜⎝(N+12)λD⎞⎟ ⎟⎠
A transparent glass plate of thickness 0.5 mm and refractive index 1.5 is placed infront of one of the slits in a double slit experiment. If the wavelength of light used is 6000A∘, the ratio of maximum to minimum intensity in the interference pattern is 25/4. Then the ratio of light intensity transmitted to incident on thin transparent glass plate is
View SolutionA monochromatic light of λ=5000Å is incident on two identical slits separated by a distance of 5×10−4 m. The interference pattern is seen on a screen placed at a distance of 1 m from the plane of slits. A thin glass plate of thickness 1.5×10−6 m and refractive index μ=1.5 is placed between one of the slits and the screen . Find the intensity at the center of the screen.
View SolutionLight of wavelength λ=5000Å falls normally on a narrow slit. A screen is placed at a distance of 1m from the slit and perpendicular to the direction of light. The first minima of the diffraction pattern is situated at 5mm from the centre of central maximum. The width of the slit is
View SolutionA young's double slit apporatus is immersed in a liquid of refractive index 1.33.It has slit separation of 1 mm and interference pattern is observed on the screen at a distance 1.33 m from plane of slits.The wavelength in air is 6300Å
Calculate the fringe width.
View SolutionA YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)
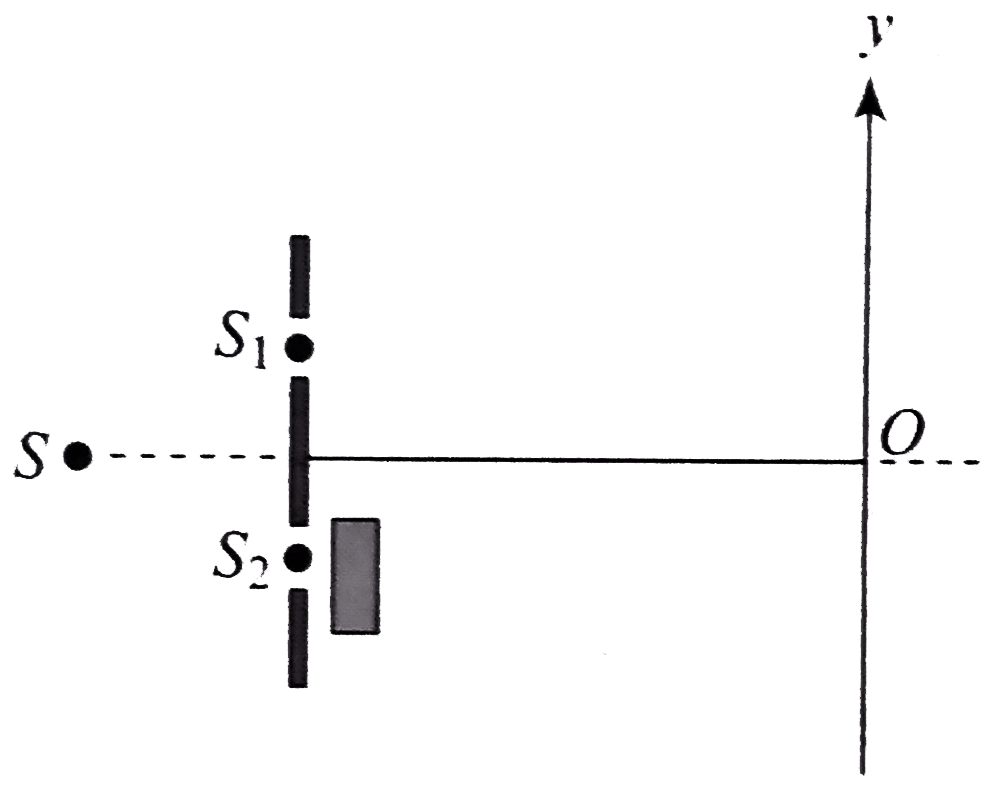
Find the light intensity at point O relative t maximum fringe intensity.
View SolutionA beam of light of wavelength 400 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 2 m away from the slit. It is observed that 2nd order minima occurs at a distance of 2 mm from the position of central maxima. Find the width of the slit.
View SolutionLight of wavelength 6×10−5 cm falls on screen at a distance of 100 cm from a narrow slit. Find the width of the slit if the first minima lies 1mm on either side of the central maximum
View Solution
