A plane monochromatic light wave falls normally on a diaphragm with two narrow slits separated by 2.5mm. The fringe pattern is formed on a screen 100 cm behind the diaphragm. By what distance will these fringes be displaced, when one of the slits is covered by a glass plate (μ=1.5) of thickness 10μm?
2mm
1mm
3mm
4mm
The correct Answer is:A
To solve the problem step by step, we will calculate the displacement of the fringe pattern when one of the slits is covered by a glass plate.
Step 1: Calculate the optical path difference introduced by the glass plate.
The formula for the optical path difference (Δ) when a glass plate of thickness T and refractive index μ is introduced is given by:
Δ=(μ−1)⋅T
Given:
- μ=1.5
- T=10μm=10×10−6m
Substituting the values:
Δ=(1.5−1)⋅(10×10−6)=0.5⋅(10×10−6)=5×10−6m
Step 2: Calculate the displacement of the fringe pattern on the screen.
The displacement of the fringe pattern (Δx) on the screen can be calculated using the formula:
Δx=Δ⋅Dd
Where:
- D = distance from the slits to the screen = 100 cm = 1 m
- d = separation between the slits = 2.5 mm = 2.5 \times 10^{-3} \, m
Substituting the values:
Δx=5×10−6⋅12.5×10−3=5×10−62.5×10−3=2×10−3m
Step 3: Convert the displacement into millimeters.
Since 1m=1000mm:
Δx=2×10−3m=2mm
Final Answer:
The fringes will be displaced by 2 mm.
---
- μ=1.5
- T=10μm=10×10−6m
- D = distance from the slits to the screen = 100 cm = 1 m
- d = separation between the slits = 2.5 mm = 2.5 \times 10^{-3} \, m
The fringes will be displaced by 2 mm.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Objective question2videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 1Subjective22videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 1 Assertion And Reason10videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
Similar Questions
Monochromatic light from a narrow slit illuminates two parallel slits producing an interference pattern on a screen. The separation between the two slits is now doubled and the distance between the screen and the slits is reduced to half. The fringe width
View SolutionA monochromatic light of λ=5000Å is incident on two identical slits separated by a distance of 5×10−4 m. The interference pattern is seen on a screen placed at a distance of 1 m from the plane of slits. A thin glass plate of thickness 1.5×10−6 m and refractive index μ=1.5 is placed between one of the slits and the screen . Find the intensity at the center of the screen.
View SolutionA monochromatic light of λ=500nm is incident on two identical slits separated by a distance of 5×10−4m. The interference pattern is seen on a screen placed at a distance of 1m from the plane of slits. A thin glass plate of thickness 1.5×10−6m and refractive index μ=1.5 is placed between one of the slits and the screen. Find the intensity at the center of the screen if the intensity is I0 in the absence of the plate. Also find the lateral shift of the central maxima and number of fringes crossed through center.
View SolutionMonochromatic green light of wavelength 5×10−7m illuminates a pair of slits 1 mm apart. The separation of bright lines on the interference pattern formed on a screen 2 m away is
View SolutionMonochromatic green light of wavelength 5×10−7m illuminates a pair of slits 1 mm apart. The separation of bright lines on the interference pattern formed on a screen 2 m away is
View SolutionIn Young's experiment, monochromatic light is used to illuminate the two slits A and B. Interference fringes are observed on a screen placed in front of the slits. Now if a thin glass plate is placed normally in the path of the beam coming from the slit
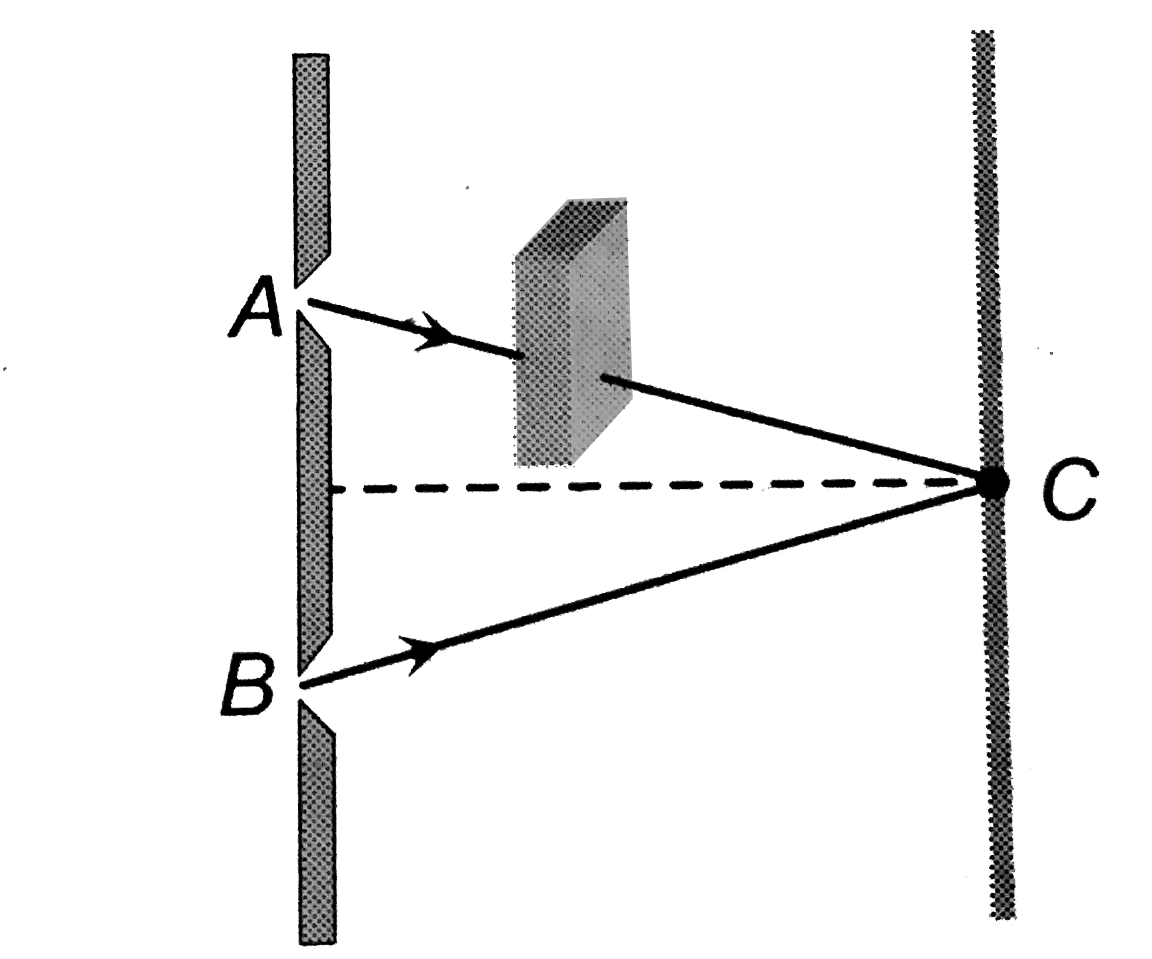 View Solution
View SolutionIn Young's experiment, monochromatic light is used to illuminate the two slits A and B. Interference fringes are observed on a screen placed in front of the slits. Now if a thin glass plate is placed normally in the path of the beam coming from the slit
 View Solution
View SolutionTwo slits in YDSE are placed 1 mm from each other. Interference pattern is observed on a screen placed 1m from the plane of slits. What is the angular fringe width for a light of wavelength 400 nm
View SolutionIn a Young's double slit experiment, a parallel beam containing wavelengths λ1=4000Å and λ2=5600Å is incident at an angle ϕ=30∘ on a diaphragm having narrow slits at separation d=2mm. The screen is placed at a distance D =40 cm from the slits. a mica slab of thickness t=5mm is placed in front of one of the slits and whole of the apparatus is submerged in water. if the central bright fringe is observed at C, determine.

(i) The refractive index of the slab
(ii) The distance of first black line from C
both wavelength are in air. take μw=43View SolutionTwo slits in YDSE are placed 2 millimeter from each other. Interference pattern is observed on a screen placed 2 m from the plane of slits. What is the fringe width for a light of wavelength 400 nm?
View Solution
