In the set up shown in figure dltltD and d=4lambda, find.
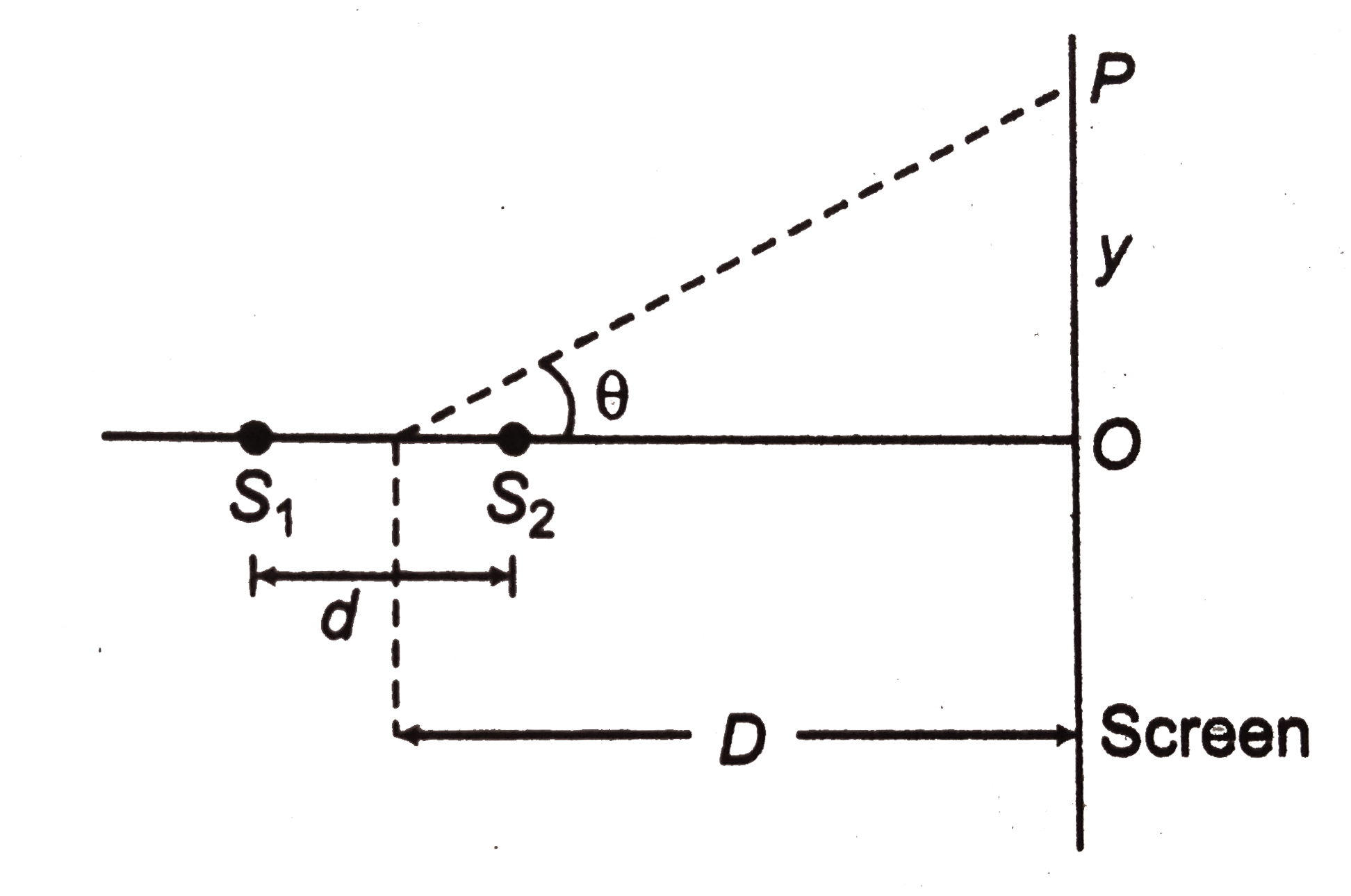
(a) total number of maximas and minimas on the screen
(b) y-coordinates corresponding to minima nearest to O.
(a) In the given set up, dltltD , therefore we can use
Δx=dcosθ
(Δx)min=0at θ=90∘
(Δx)max=d=4λ at θ=0∘
Therefore, total number of maximas are eight corresponding to
Δx=±4λ,±3λ,±2λand±λ
(b) Minima nearest to O are corresponding to
Δx=±3.5λ
∴dcosθ=±3.5λor4λcosθ=±3.5λ
or θ=±cos−1(3.5λ4λ) or θ=±cos−1(78)
Now, yD=tanθ⇒y=Dtanθ
∴y=±Dtan{cos−1(78)} .
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:INTERFERENCE AND DIFFRACTION OF LIGHTExercise:type-3
Explore 1 Video
- INTERFERENCE AND DIFFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:INTERFERENCE AND DIFFRACTION OF LIGHTExercise:Example Type 4
Explore 1 Video
- INTERFERENCE AND DIFFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:INTERFERENCE AND DIFFRACTION OF LIGHTExercise:Example Type 2
Explore 2 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:All Questions
Explore 135 Videos
- MAGNETIC FIELD AND FORCESBook:DC PANDEY ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
Similar Questions
In the YDSE apparatus shown in figure, d<<D and d=6λ. Find

(a) total number of maximas and minimas on the screen .
(b) two y-coordinates corresponding to third order maxima.
View SolutionThere is a large circle (not a screen this time) around two coherent
sources S1 and S2 kept at a distance d=3.4λ.
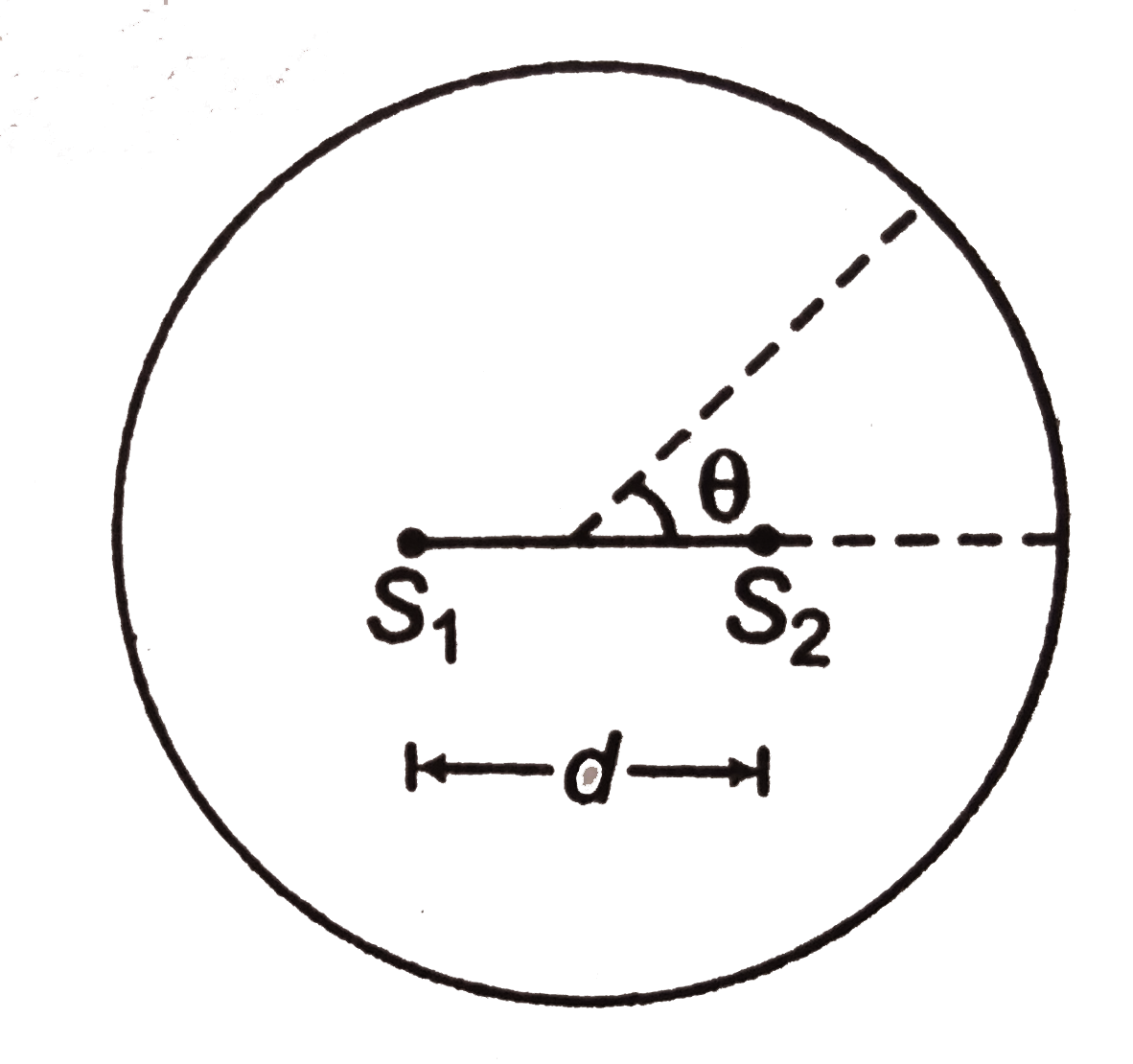
(a) Find total number of maximas on this circle.
(b) Four angular positions corresponding to third order maxima on this circle.
View SolutionAssertion: In the YDSE apparatus shown in figure dltltD and dλ=4, then second order maxima will be obtained at θ=30∘
Reason: Total seven maxima will be obtained on screen.
View SolutionIn a Young's double slit experiment, the light sources is at distance l1=20μm and l2=40μm form the main slit. The light of wavelength lambda = 500nm is incident on slits separated at a distance 10μm. A screen is placed at a distance D = 2 away from the slits as shown in figure. Find
(a) the values of θ relative to the central line where maxima appear on the screen?
(b) how many maxima will appear on the screen?
what should be the minimum thickness of a slab of refractive index 1.5 placed on the path of one of the ray so that minima occurs at C ?
 .
.
View SolutionStatement I: For the situation shown in figure two identecal coherent light sources produce interference pattern on the screen. The intensity of minima nearest to S1 is not exactly zero.

Statement II: Minimum intensity is zero, when interfering waves have same intensity at the location of superposition.
View SolutionIn a YDSE, D=1M,d=1mm,andλ=1/2mm.
(a) Find the distance between the first and central maxima on the screen.
(b) Find the number of maxima and minima obtained on the screen.
View SolutionAssertion: Distance between two coherent sources S1andS2 is 4λ. A large circle is drawn around these sources with centre of circle lying at centre of S1andS2. There are total 16 maxima on this circle.
Reason: Total number of minimas on this circle are less, compared to total number of maximas.
View SolutionA coherent parallel beam of microwaves of wavelength λ=0.5mm falls on aYoung's double- slit apparatus. The separation between the slits is 1.0 mm. The intensity of microwaves is measured on a screen placed parallel to the plane of the slits at a distance of 1.0 m from it as shown in Fig. 2.42.
If the incident beam makes an angle or 30∘ with the x-axis (as in the dotted arrow shown in the figure), find the y-coordinates of the first minima on either side of the central maximum.
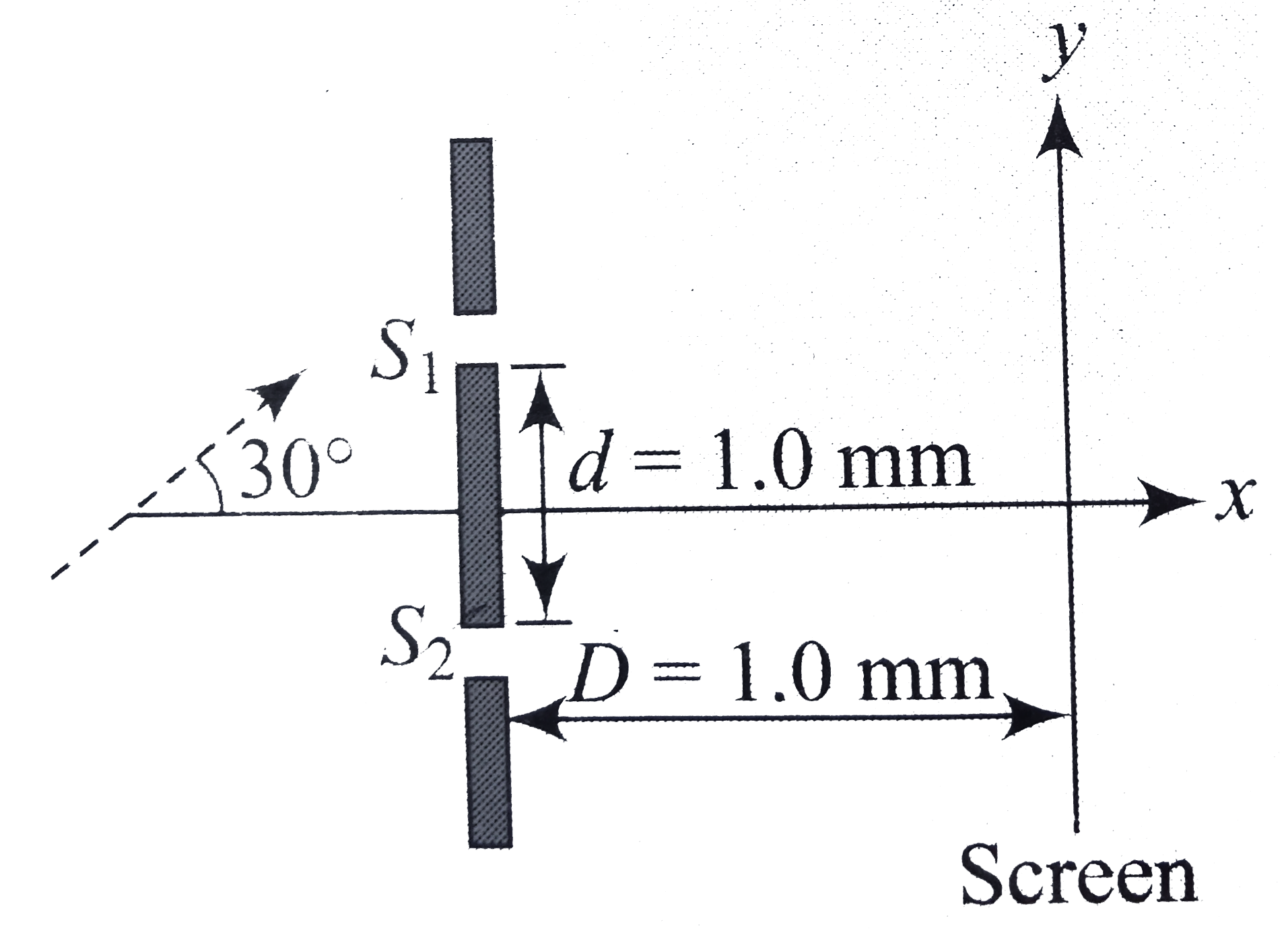
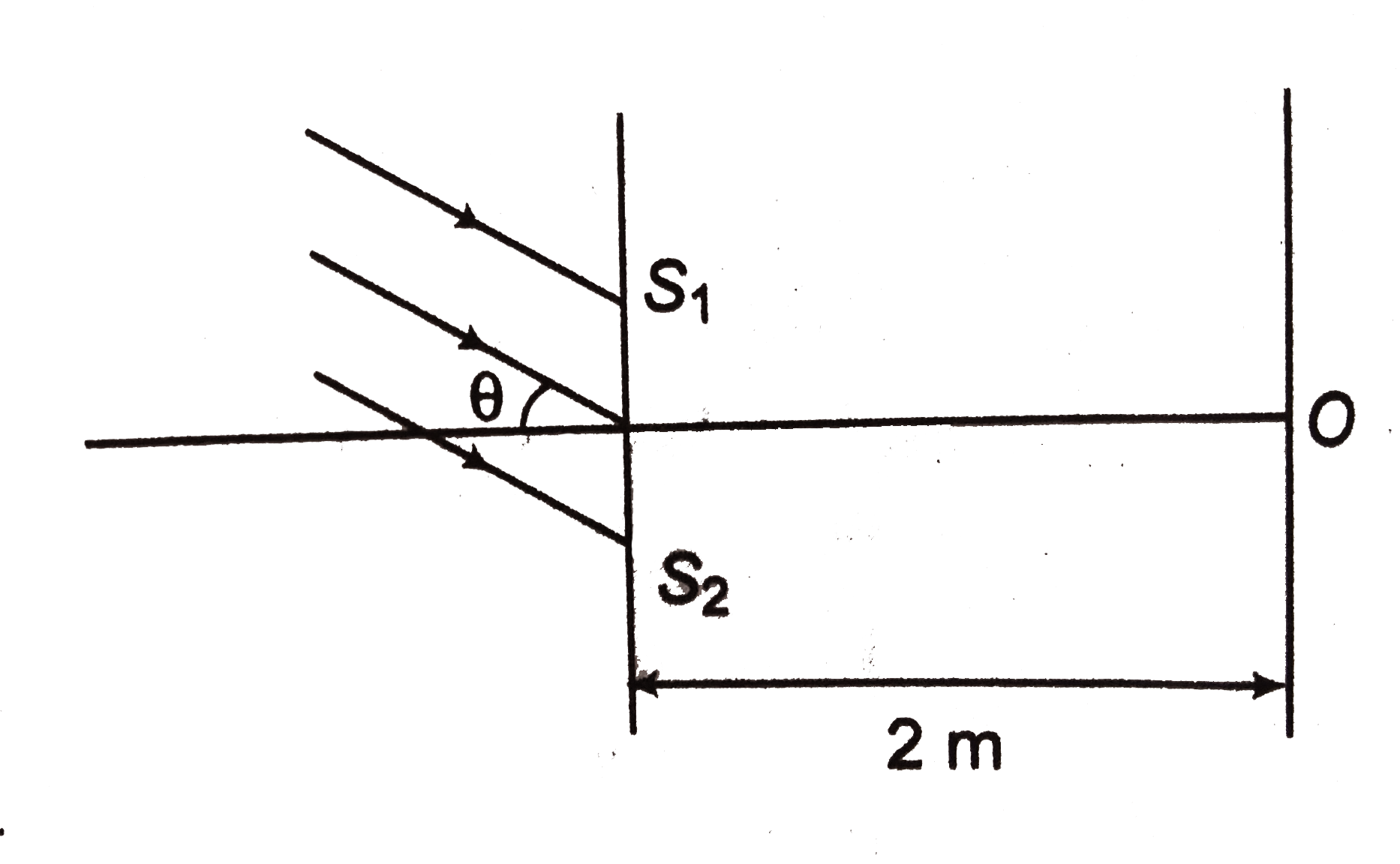
View SolutionA parallel beam of light (λ=5000Å) is incident at an angle θ=30∘ with the normal to the slit plane in a Young's double slit experiment. The intensity due to each slit is I0. Point O is equidistant from S1andS2. The distance between slits is 1mm.
View SolutionAssertion In the YDSE set up shown in figure a glass slab is inserted in front of the slit S1 as shown in figure Then zero order maxima (where path difference =0) will lie above point O.
Reason Glass slab will produce an extra path difference in the path of the ray passing through S1
View Solution