An object O is just about to strike a perfectly reflecting inclined plane of inclination 37∘. Its velocity is 5m/s. Find the velocity of its image.
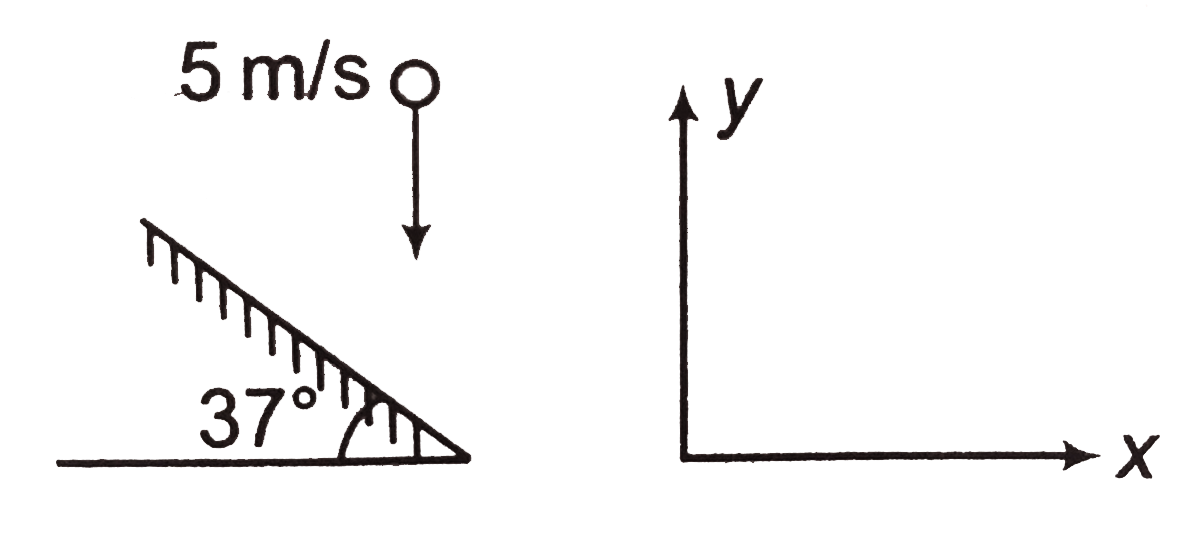
3(ˆi)+4(ˆj)
4(ˆi)+3(ˆj)
4.8(ˆi)+1.4(ˆj)
1.4(ˆi)+4.8(ˆj)
The correct Answer is:C
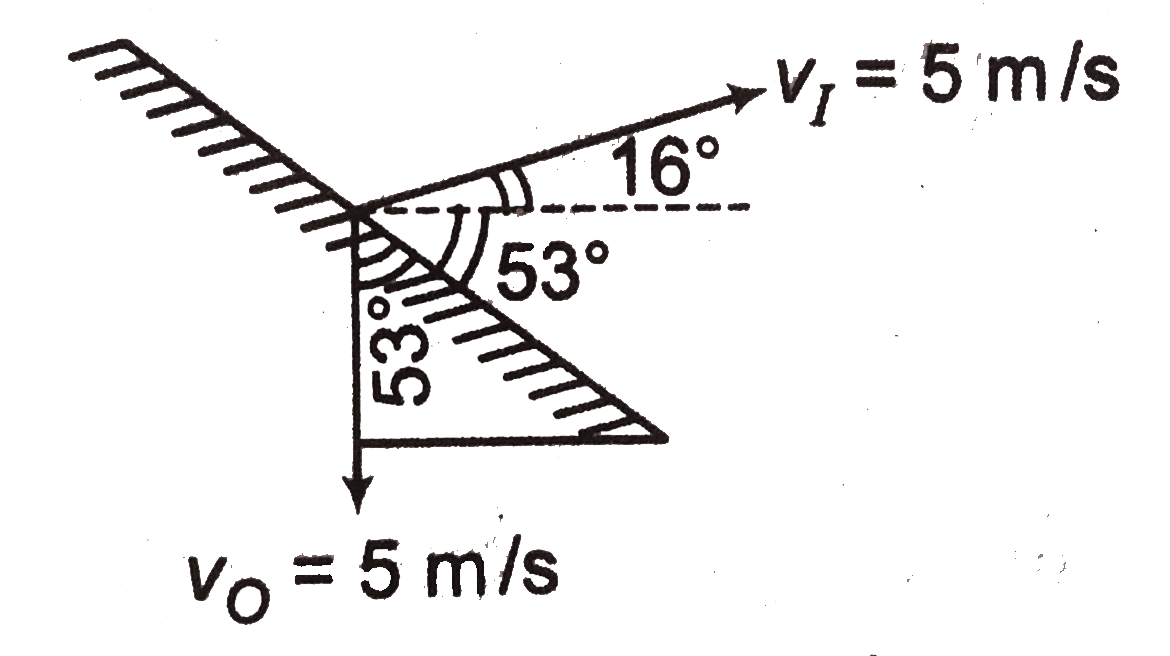
vo=5m/s
vI=(5cos16∘)ˆi+(5sin16∘)ˆj
=(4.8ˆi+1.4ˆj)m/s.
Topper's Solved these Questions
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Level 2 More Than One Correct
6 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Level 2 Comprehensive Based
4 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Exercise Level 1 Subjective
17 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
A particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
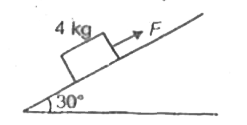
View SolutionA block of mass 4 kg is pulled along a smooth inclined plane of inclination 30∘ with constant velocity 3 m/s as shown, power delivered by the force is
View SolutionA Sphere pure rolls on a rough inclined plane with initial velocity 2.8 m/s. Find the maximum distance on the inclined plane

View SolutionConsider a point object moving towards a stationary plane mirror with velocity 5m/s. Find velocity of image w.r.t object
View SolutionA block moves down a smooth inclined plane of inclination θ. Its velocity on reaching the bottom is v. If it slides down a rough inclined plane of some inclination, its velocity on reaching the bottom is v/n, where n is a number greater than 0. The coefficient of friction is given by -
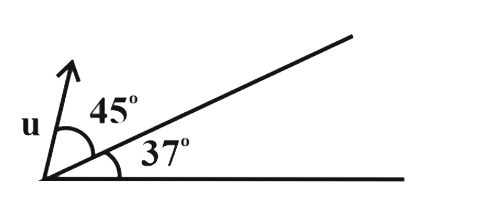
View SolutionA particle is projected on a frictionless inclined plane of inclination 37∘ at an angle of projection 45∘ from the inclined plane as shown in the figure. If after the first collision from the plane, the particle returns to its point of projection, then what is the value of the reciprocal of the coefficient of restitution between the particle and the plane?
View SolutionA small ball falling vertically downward with constant velocity 2m/s strikes elastically an inclined plane moving with velocity 2m/s as shown in figure. The velocity of rebound of the ball with respect ground is
(A)4m/s (B)2√5m/s (C)2√2m/s (D)2m/s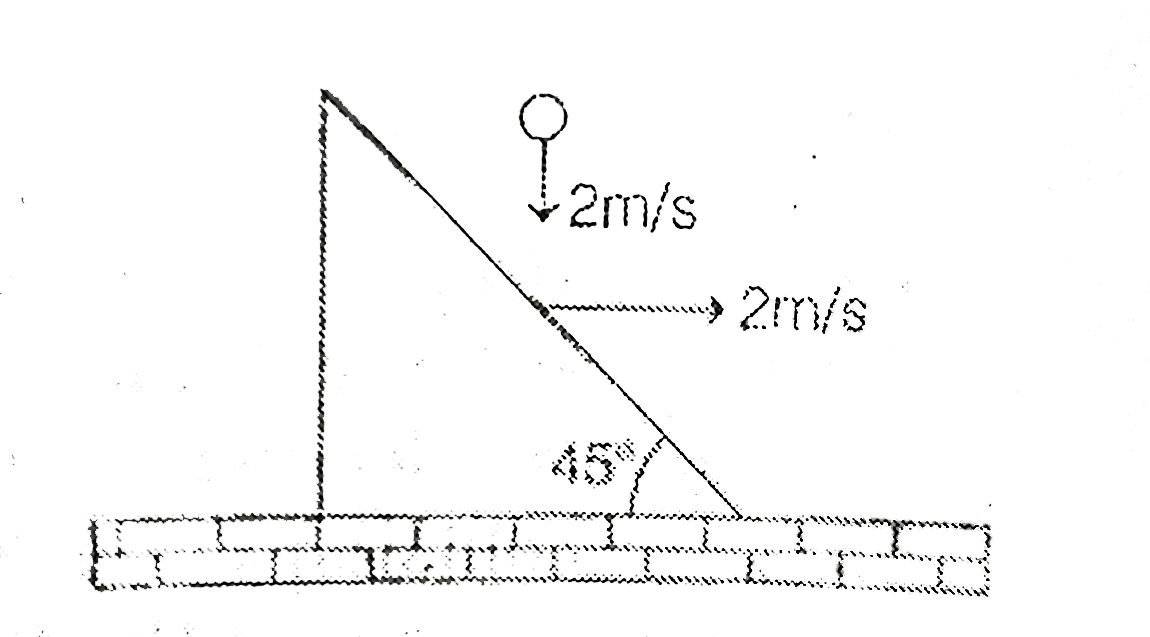
View SolutionA projectile si thrown with velocity of 50m/s towards an inclined plane from ground such that is strikes the inclined plane perpendiclularly. The angle of projection of the projectile is 53∘ with the horizontal and the inclined plane is inclined at an angle of 45∘ to the horizonta..

(a) Find the time of flight.
(b) Find the distance between the point of projection and the foot of inclined plane.
View SolutionA particle is projected with a certain velocity at an angle ∝ above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally, then ∝ is equal to.
View SolutionA particle is projected with a certain velocity at an angle α above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally then α is equal to
View Solution
