It is known to all of you that the impedance of a circuit is dependent on the frequency of source. In order to study the effect of frequency on the impedance, a student in a lab took 2 impedance boxes P and Q and connected them in series with an AC source of variable frequency. The emf of the source is constant at 10V Box P contains a capacitance of 1μF in series with a resistance of 32Ω. And the box Q has a coil of self-inductance 4.9mH and a resistance of 68Ωin series. He adjusted the frequency so that the maximum current flows in P and Q. Based on his experimental set up and the reading by him at various moment, answer the following questions.
Impedance of box P at the above frequency is
70Ω
77Ω
90Ω
100Ω
The correct Answer is:B
To find the impedance of box P at the frequency where maximum current flows, we will follow these steps:
1. Identify the Components of Box P:
- Box P contains a capacitance C=1μF=1×10−6F in series with a resistance RP=32Ω.
2. Determine the Condition for Maximum Current:
- Maximum current in an AC circuit occurs when the circuit is at resonance. At resonance, the capacitive reactance XC and inductive reactance XL are equal.
3. Calculate the Capacitive Reactance XC:
- The capacitive reactance is given by the formula:
XC=1ωC
- To find ω (angular frequency), we need to use the relationship at resonance, which is:
ω=1√LC
- However, we do not have the inductance L for box P, but we can still calculate XC directly using the frequency that gives maximum current.
4. Determine the Frequency f:
- From the video, it is stated that the frequency is related to the inductance of box Q. The inductance L=4.9mH=4.9×10−3H.
- The resonant frequency f can be calculated as:
f=12π√LC
- Substituting L and C:
f=12π√4.9×10−3×1×10−6
5. Calculate ω:
- Convert frequency to angular frequency:
ω=2πf
6. Calculate XC:
- Substitute ω back into the capacitive reactance formula:
XC=1ωC
7. Calculate the Impedance ZP:
- The impedance of box P is given by:
ZP=√R2P+X2C
- Substitute RP and XC to find ZP.
8. Final Calculation:
- After performing the calculations, you will find ZP.
Final Answer:
The impedance of box P is approximately ZP≈77Ω.
---
- Box P contains a capacitance C=1μF=1×10−6F in series with a resistance RP=32Ω.
- Maximum current in an AC circuit occurs when the circuit is at resonance. At resonance, the capacitive reactance XC and inductive reactance XL are equal.
- The capacitive reactance is given by the formula:
XC=1ωC
- To find ω (angular frequency), we need to use the relationship at resonance, which is:
ω=1√LC
- However, we do not have the inductance L for box P, but we can still calculate XC directly using the frequency that gives maximum current.
- From the video, it is stated that the frequency is related to the inductance of box Q. The inductance L=4.9mH=4.9×10−3H.
- The resonant frequency f can be calculated as:
f=12π√LC
- Substituting L and C:
f=12π√4.9×10−3×1×10−6
- Convert frequency to angular frequency:
ω=2πf
- Substitute ω back into the capacitive reactance formula:
XC=1ωC
- The impedance of box P is given by:
ZP=√R2P+X2C
- Substitute RP and XC to find ZP.
- After performing the calculations, you will find ZP.
The impedance of box P is approximately ZP≈77Ω.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level 2 Subjective
10 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - JEE MAIN
62 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level- 2More Than One Correct
8 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
Similar Questions
It is known to all of you that the impedance of a circuit is dependent on the frequency of source. In order to study the effect of frequency on the impedance, a student in a lab took 2 impedance boxes P and Q and connected them in series with an AC source of variable frequency. The emf of the source is constant at 10V Box P contains a capacitance of 1μF in series with a resistance of 32Ω. And the box Q has a coil of self-inductance 4.9mH and a resistance of 68Ωin series. He adjusted the frequency so that the maximum current flows in P and Q. Based on his experimental set up and the reading by him at various moment, answer the following questions.
Power factor of the circuit at maximum current is
View SolutionIt is known to all of you that the impedance of a circuit is dependent on the frequency of source. In order to study the effect of frequency on the impedance, a student in a lab took 2 impedance boxes P and Q and connected them in series with an AC source of variable frequency. The emf of the source is constant at 10V Box P contains a capacitance of 1μF in series with a resistance of 32Ω. And the box Q has a coil of self-inductance 4.9mH and a resistance of 68Ωin series. He adjusted the frequency so that the maximum current flows in P and Q. Based on his experimental set up and the reading by him at various moment, answer the following questions.
The angular frequency foer which he detects maximum current in the circuit is
View Solution
Knowledge Check
A box P and a coil Q are connected in series with an ac source of variable frequency. The emf of the source is constant at 10 V. Box P xontains a capacitance of 32Ω. Coil Q has a self inductance of 4.9 mH and a resistance of 68Ω in series. The frequency is adjusted so that maximum current flows in P and Q.
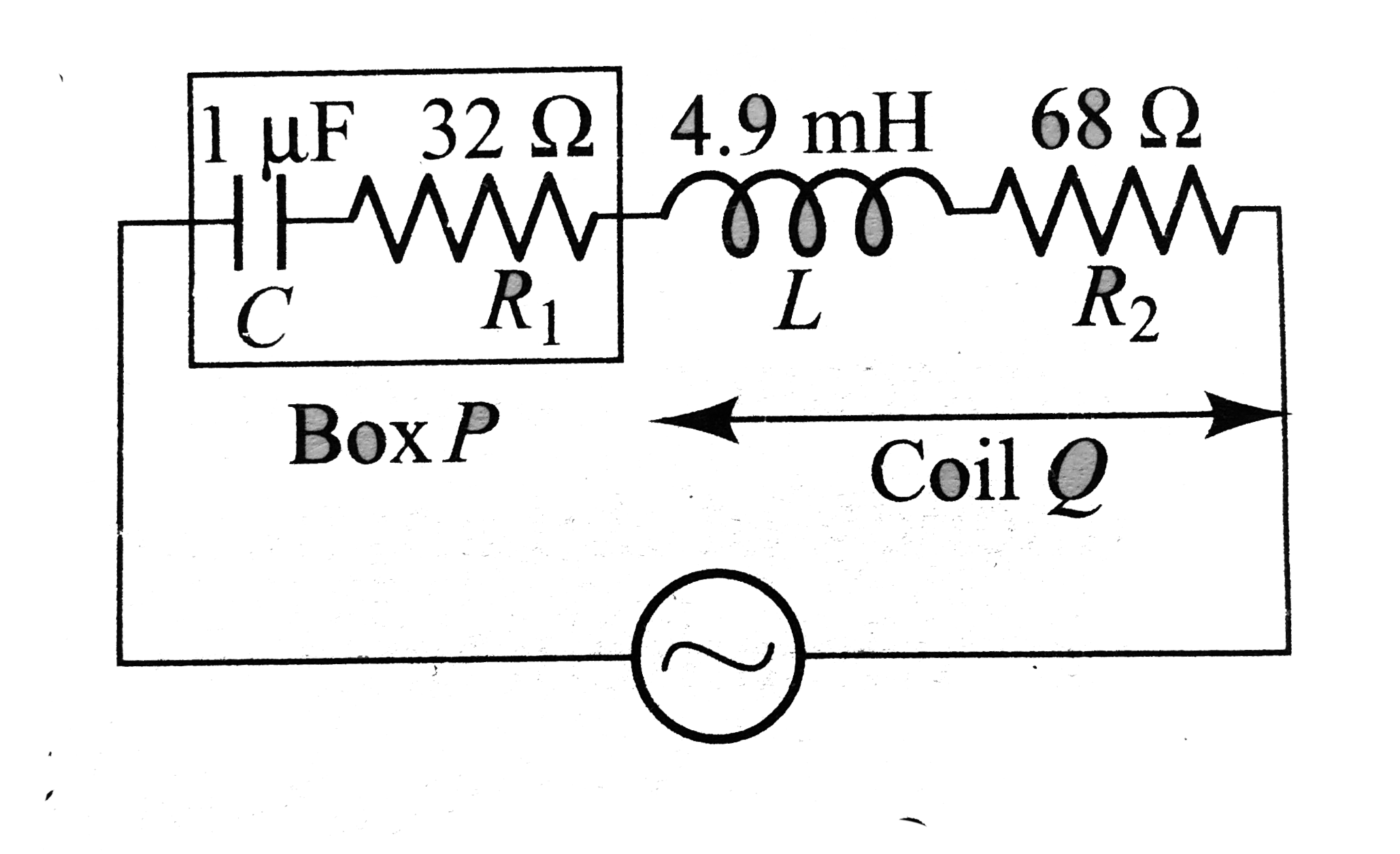
The impendance of Q at this frequency isA9.76V,8.92VB6.29V,7.96VC7.70V,10.92VD7.70V,9.76V
A box P and a coil Q are connected in series with an ac source of variable frequency. The emf of the source is constant at 10 V. Box P contains a capacitance 1μf and a resistance of 32Ω. Coil Q has a self inductance of 4.9 mH and a resistance of 68Ω in series. The frequency is adjusted so that maximum current flows in P and Q.
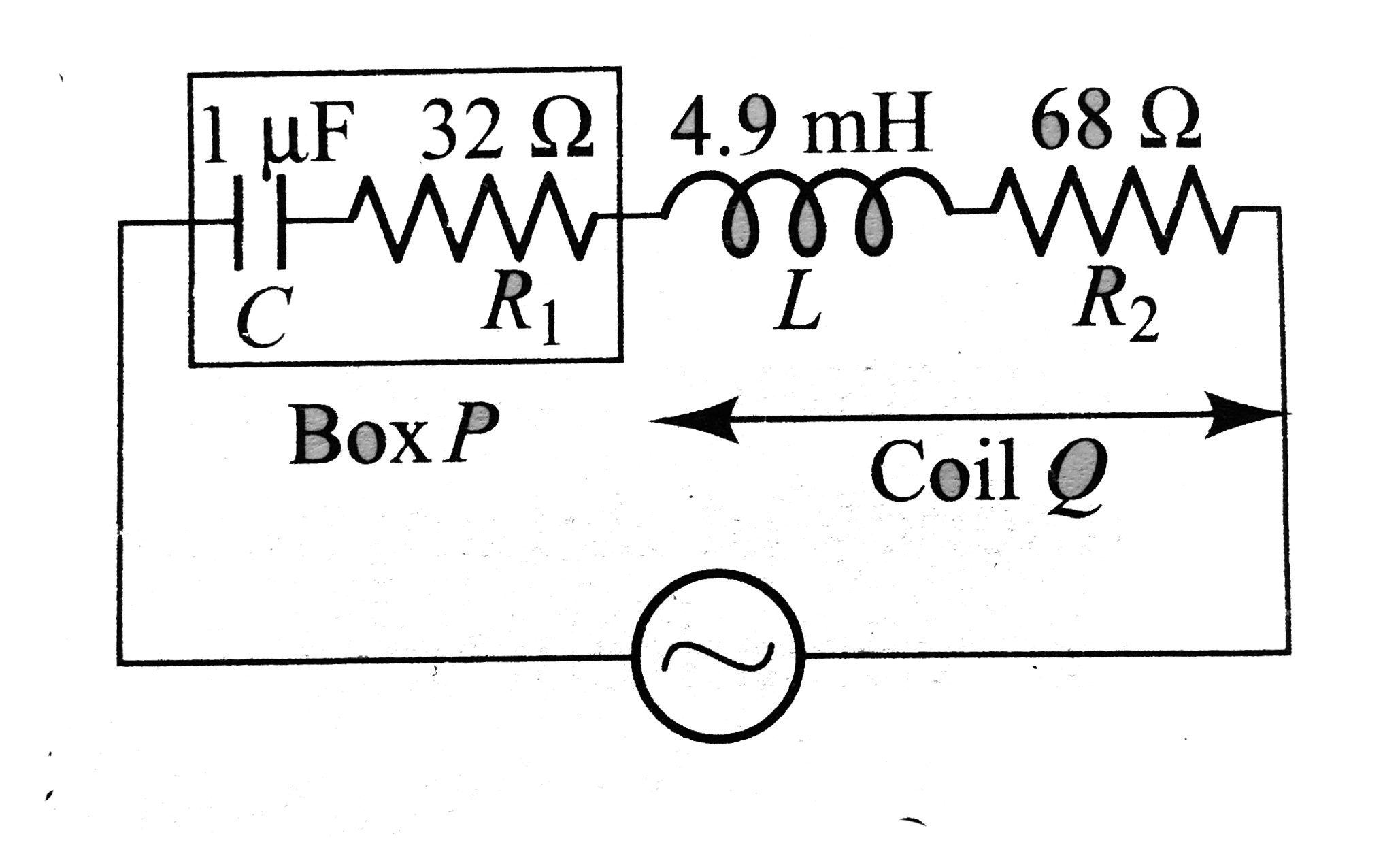
The voltage across P is
View SolutionA box P and a coil Q are connected in series with an AC source of variable frequency.The EMF of source is constant at 10V.Box P contains a capacitance of 1μF in series with a resistance of 32Ω.Coil Q has a self inductance 4.9mH and a resistance of 68Ω.The frequency is adjusted so that the maximum current flows in P and Q.Find the impedance of P and Q at this frequency.Also find the voltage across P and Q respectively.
View SolutionA box P and a coil Q are connected in series with an ac source of variable frequency. The emf of the source is constant at 10 V. Box P contains a capacitance of 32Ω. Coil Q has a self inductance of 4.9 mH and a resistance of 68Ω in series. The frequency is adjusted so that maximum current flows in P and Q.
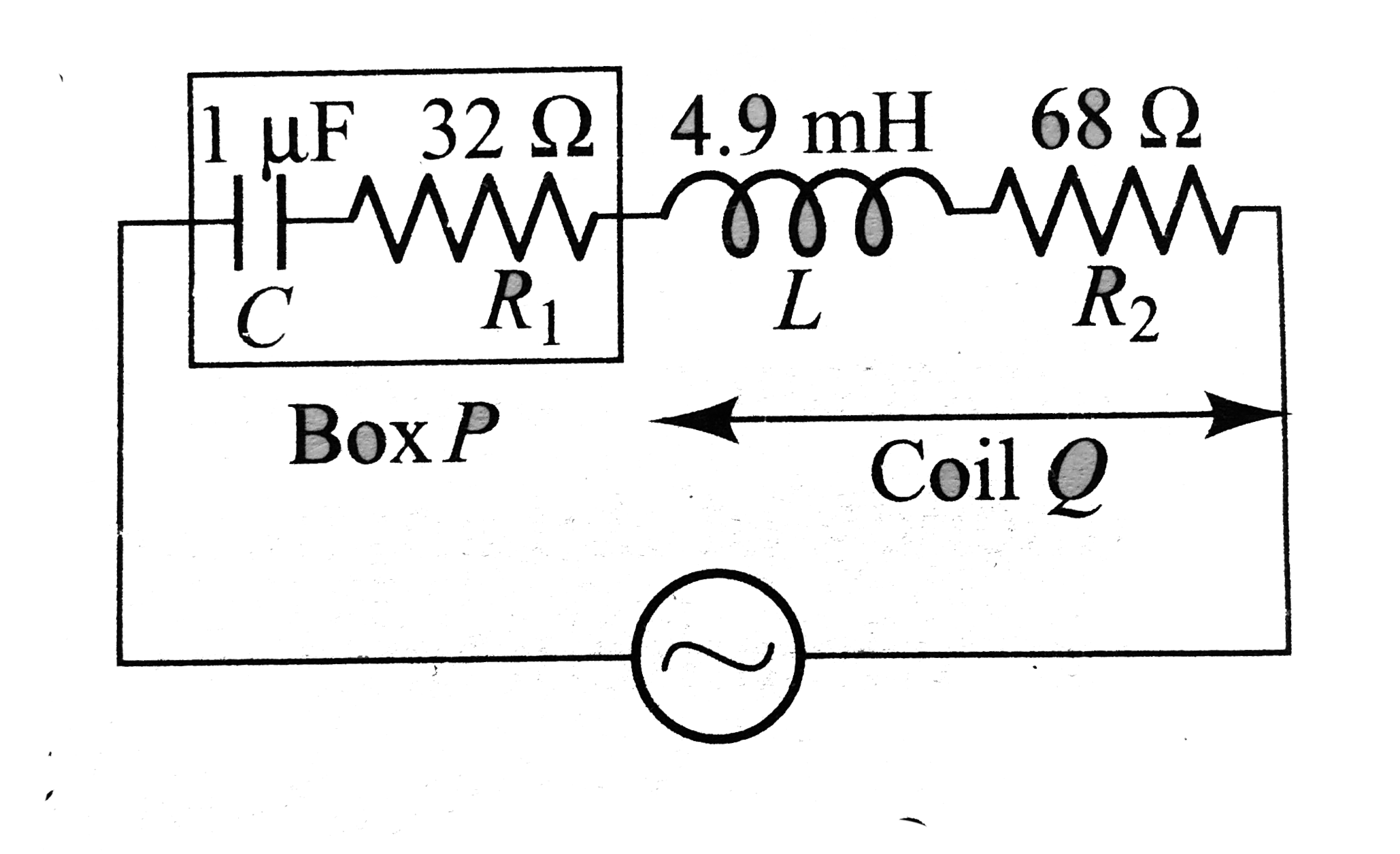
The impedance of P at this frequency is
View SolutionA bulb and a conender are connected in series with an A.C source. On increasing the frequency of the source its brightness will
View SolutionFor an LCR series circuit with an aac source of angular frequency ω.
View SolutionFor an LCR series circuit with an ac source of angular frequency ω.
View SolutionA box P and a coil Q are connected in series with an ac source of variable freguency The emf of the source is constant at 28V The frequency is so adjusted that the maximum current flows in P and Q Find
(a) impedance of P and Q at this frequency
(b) voltage across P and Q
 .
.
View Solution
