A pair of parallel horizontal conducting rails of negligible resistance shorted at one end is fixed on a table. The distance between the rails is L. A conducting massless rod of resistance R can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table. A mass m tied to the other end of the string hangs vertically. A constant magnetic field B exists perpendicular to the table. If the system is released from rest, calculate
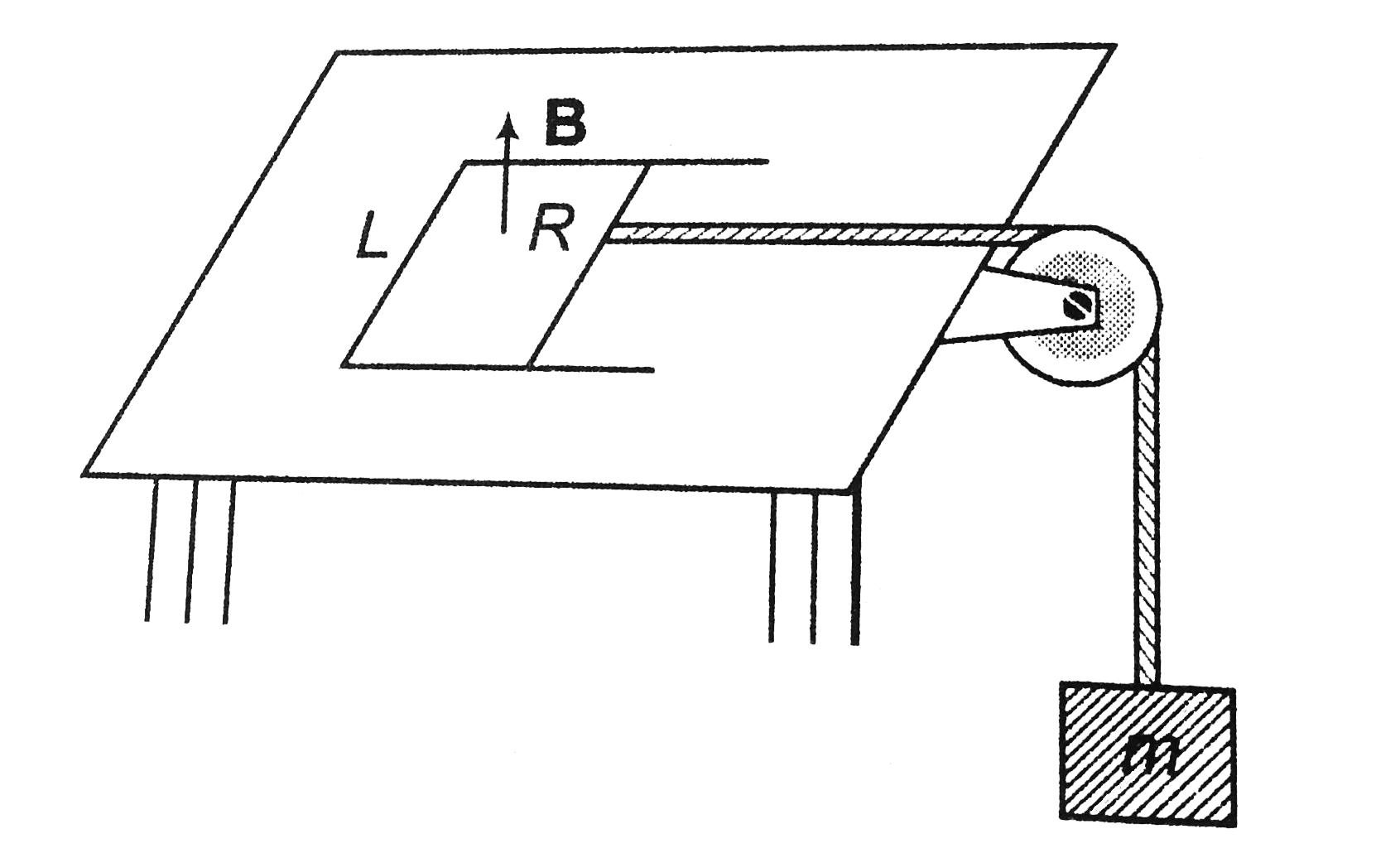
a. the terminal velocity achieved by the rod and
b. The acceleration of the mass of the instant when the velocity of the rod is half the terminal velocity.
a. Let v be the velocity of the wire (as well as block )at any instant of time t.
Motional emf e=BvL
Motional current i=er=BvLL
and magnetic force on the wire
Fm=iLB=vB2L2R
Net force on the system at this moment will be
Fnet=mg−Fm=mg−vB2L2R
ma=mg−vB2L2R
a=vB2L2mR
Velocity will acquire its terminal value i.e. v=vT when
Fnet or acceleration a of the particle becomes zero.
Thus, 0=g−vTB2L2mR
or vT=mgRB2L2
b. when v=vT2=mgR2B2L2
Then from Eqn (i) acceleratin of the block
a=g−(mgR2B2L2)(B2L2mR)=g−g2
or a=g2
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Miscellaneous Examples
Explore 5 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercise 27.1
Explore 8 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Example Type 5
Explore 2 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Medical entrances gallery
Explore 97 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
Similar Questions
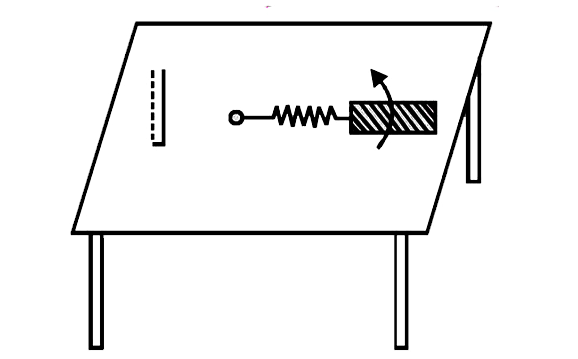
A block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
View SolutionA block of mass m is tied to a string of length L and the assembly is kept on a smooth horizontal table as shown in the figure. Now the other end of the string is moved with a constant velocity v0ˆj. (xy plane is the plane of the table) Then

View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
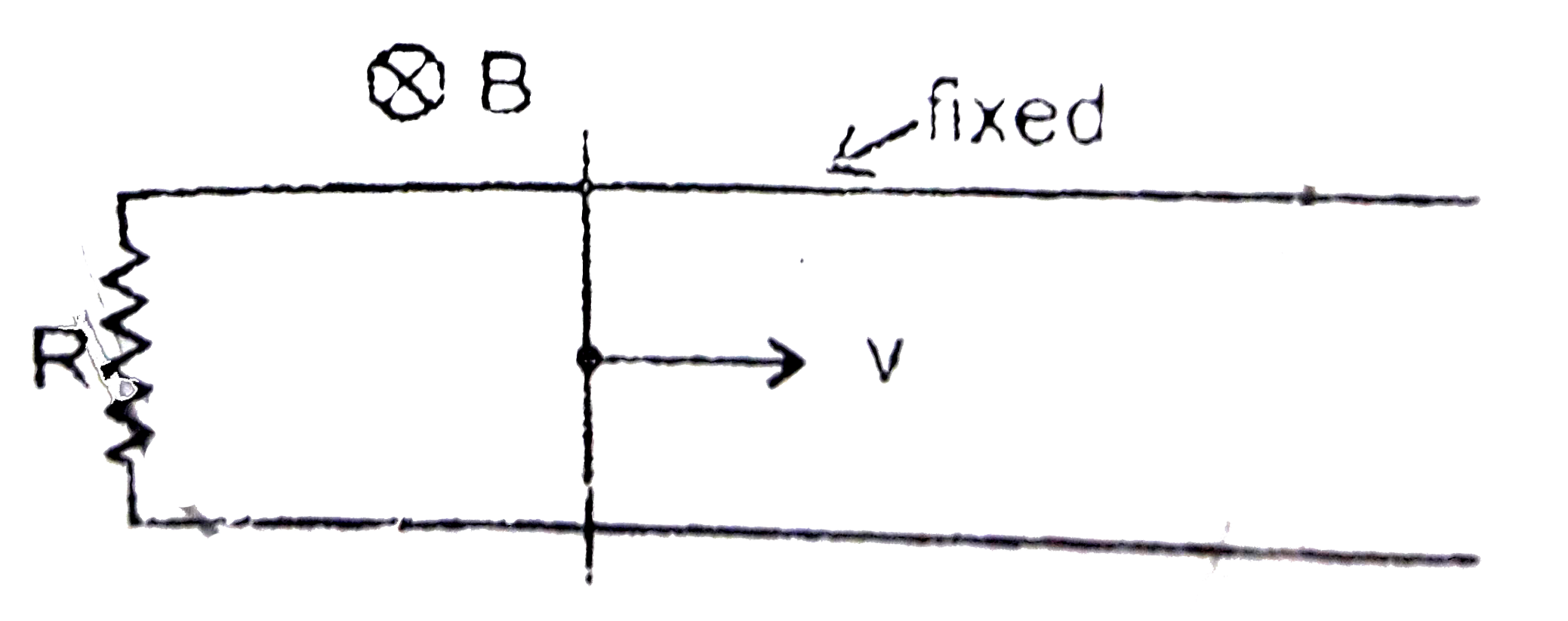
View SolutionA resistance R is connected between the two ends of the parallel smooth conducting rails.A conducting rod lies on these fixed horizontal rails and a uniform constant magnetic field B exists perpendicular to the plane of the rails as shown in the figure.If the rod is given a velocity v and released as shown in figure, it will stop after some time, which option are correct:
View SolutionA metallic rod of length 'l' is tied to a string of length 2l and made to rotate with angular speed w on a horizontal table with one end of the string fixed. If there is a vertical magnetic field 'B' in the region, the e.m.f. Induced across the ends of the rod is
View SolutionShows a wire sliding on two parallel, conducting rails placed at a separaton l. A magnetic feld B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constatn velocity v ?
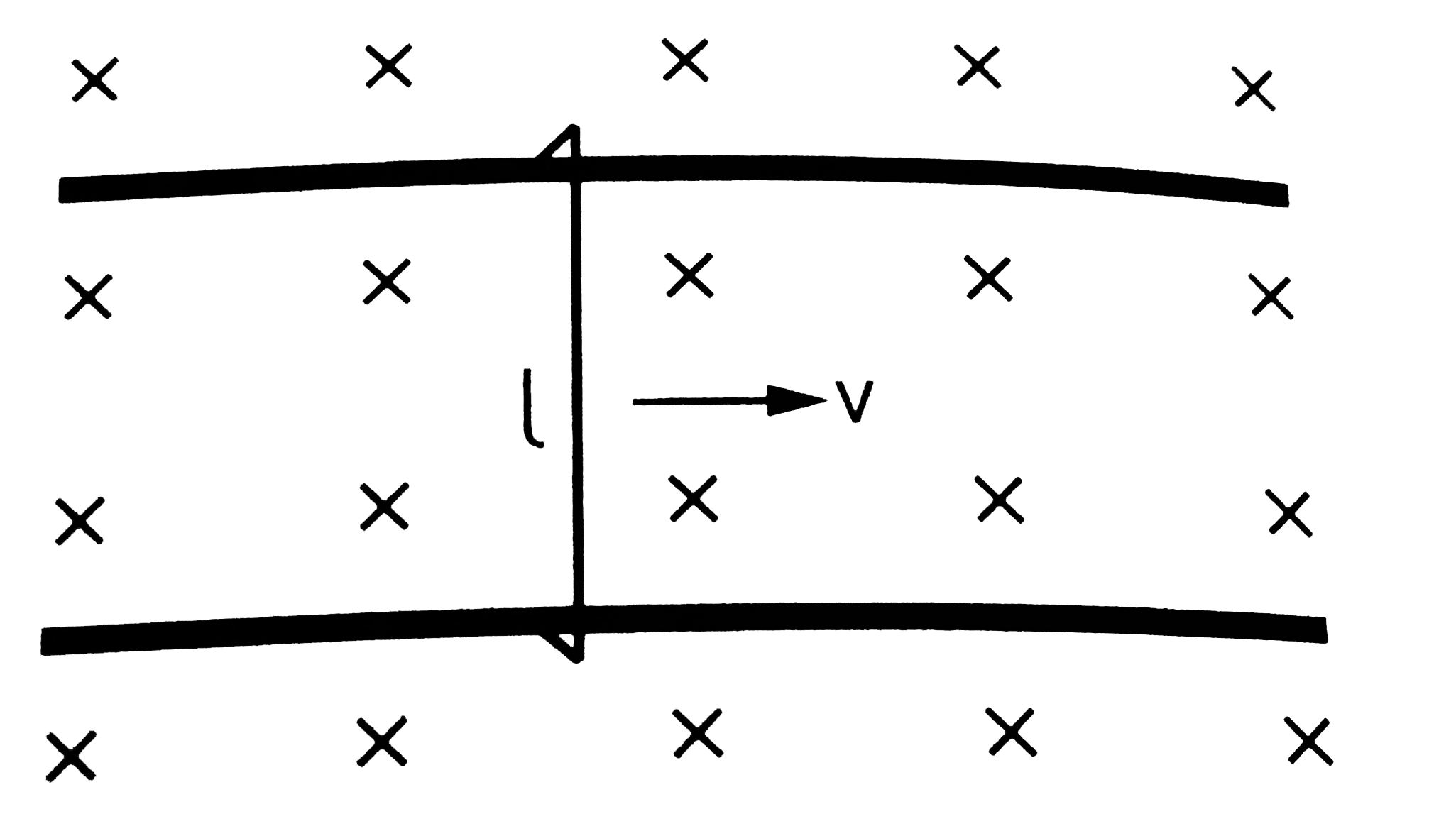
View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
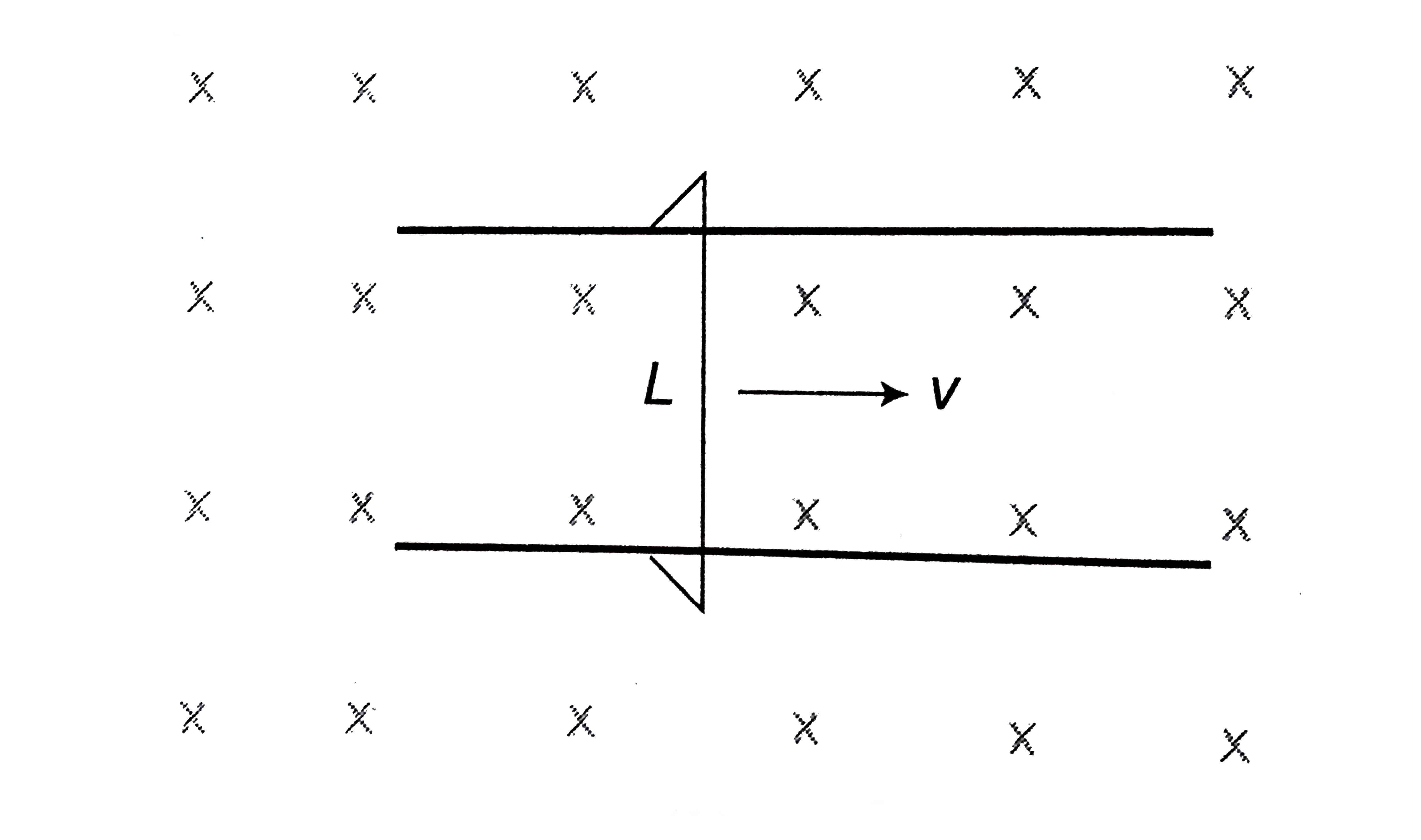
View SolutionA copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle θ to the horizontal. At the bottom, the rails are joined by a resistance R.
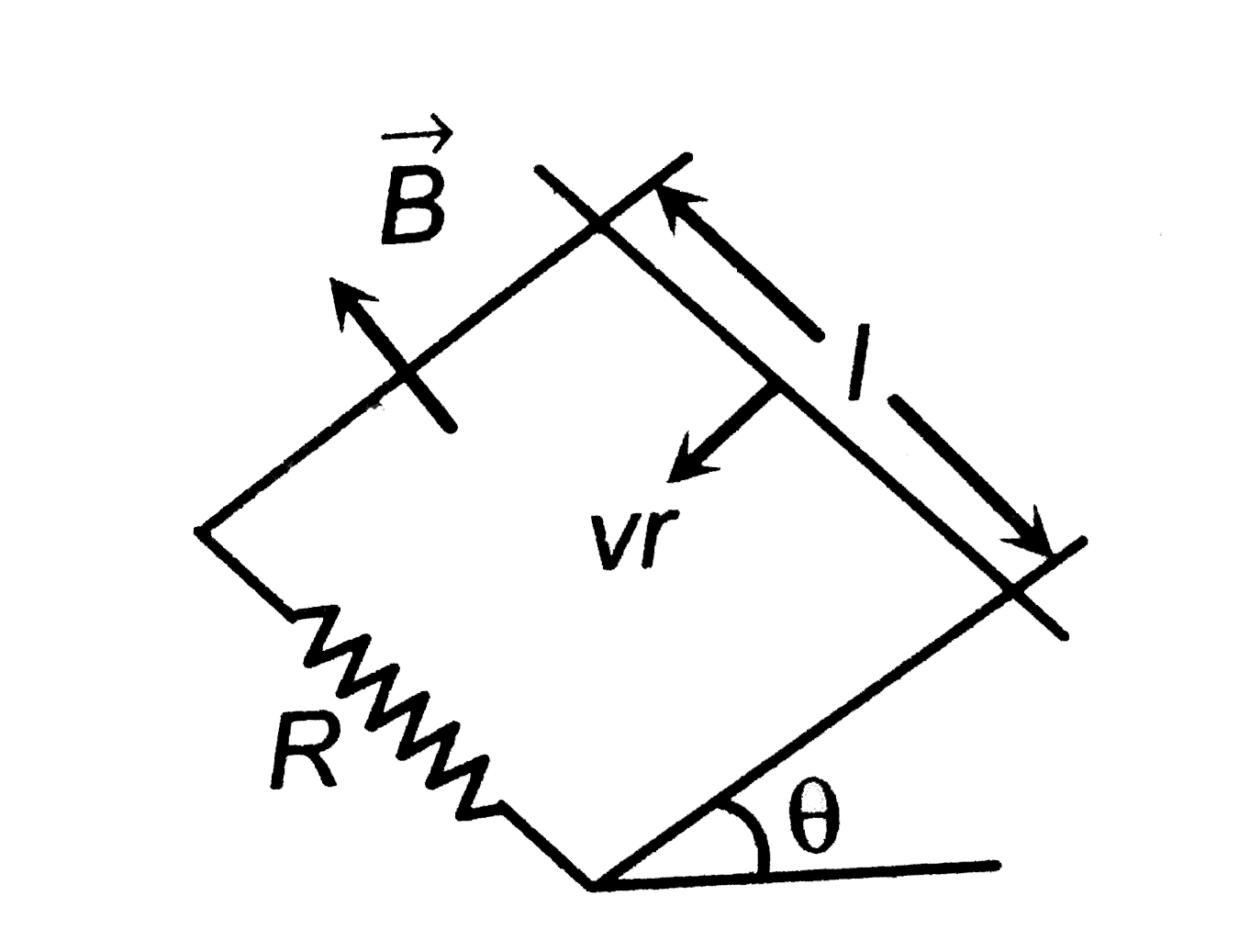
There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod is
View SolutionIn the shown figure, there are two long fixed parallel conducting rails (having negligible resistance) and are separated by distance L.A uniform rod of resistance R and mass M is placed at rest on frictionless rails. Now at time t = 0, a capacitor having charge Q0 and capacitance C is connected across rails at ends a and b such that current in rod(cd) is from c towards d and the rod is released. A uniform and constant magnetic field having magnitude B exists normal to plane of paper as shown. (Neglect acceleration due to gravity)

When the acceleration of rod is zero, the speed of rod is :
View Solution

