In an L−C circuit, L=3.3H and C=840pF. At t=0 charge on the capacitor is 105μC and maximum. Compute the following quantities at t=2.0ms.
a. The energy stored in the capacitor.
b. The total energy in the circuit,
c. The energy stored in the inductor.
To solve the problem step by step, we will compute the required quantities for the given L−C circuit.
Given Data:
- Inductance, L=3.3H
- Capacitance, C=840pF=840×10−12F
- Maximum charge on the capacitor at t=0, Q0=105μC=105×10−6C
- Time, t=2.0ms=2.0×10−3s
Step 1: Calculate the Angular Frequency (ω)
The angular frequency for an LC circuit is given by the formula:
ω=1√LC
Substituting the values:
ω=1√3.3×840×10−12
Calculating:
ω=1√2.772×10−9≈1.9×104rad/s
Step 2: Calculate the Charge on the Capacitor at t=2.0ms
The charge on the capacitor at any time t is given by:
Q(t)=Q0cos(ωt)
Substituting the values:
Q(2×10−3)=105×10−6cos(1.9×104×2×10−3)
Calculating the argument of the cosine:
ωt=1.9×104×2×10−3=38
Now, using cos(38)≈0.955:
Q(2×10−3)=105×10−6×0.955≈100.3×10−6C
Step 3: Calculate the Energy Stored in the Capacitor (UC)
The energy stored in the capacitor is given by:
UC=Q22C
Substituting the values:
UC=(100.3×10−6)22×840×10−12
Calculating:
UC=10.06009×10−121680×10−12≈6J
Step 4: Calculate the Total Energy in the Circuit (U)
The total energy in the circuit is given by the maximum energy stored in the capacitor:
U=Q202C
Substituting the maximum charge:
U=(105×10−6)22×840×10−12
Calculating:
U=11.025×10−121680×10−12≈6.56J
Step 5: Calculate the Energy Stored in the Inductor (UL)
The energy stored in the inductor can be found using:
UL=U−UC
Substituting the values:
UL=6.56J−6J=0.56J
Final Results:
- a. Energy stored in the capacitor, UC≈6J
- b. Total energy in the circuit, U≈6.56J
- c. Energy stored in the inductor, UL≈0.56J
- Inductance, L=3.3H
- Capacitance, C=840pF=840×10−12F
- Maximum charge on the capacitor at t=0, Q0=105μC=105×10−6C
- Time, t=2.0ms=2.0×10−3s
The angular frequency for an LC circuit is given by the formula:
ω=1√LC
Substituting the values:
ω=1√3.3×840×10−12
Calculating:
ω=1√2.772×10−9≈1.9×104rad/s
The charge on the capacitor at any time t is given by:
Q(t)=Q0cos(ωt)
Substituting the values:
Q(2×10−3)=105×10−6cos(1.9×104×2×10−3)
Calculating the argument of the cosine:
ωt=1.9×104×2×10−3=38
Now, using cos(38)≈0.955:
Q(2×10−3)=105×10−6×0.955≈100.3×10−6C
The energy stored in the capacitor is given by:
UC=Q22C
Substituting the values:
UC=(100.3×10−6)22×840×10−12
Calculating:
UC=10.06009×10−121680×10−12≈6J
The total energy in the circuit is given by the maximum energy stored in the capacitor:
U=Q202C
Substituting the maximum charge:
U=(105×10−6)22×840×10−12
Calculating:
U=11.025×10−121680×10−12≈6.56J
The energy stored in the inductor can be found using:
UL=U−UC
Substituting the values:
UL=6.56J−6J=0.56J
- a. Energy stored in the capacitor, UC≈6J
- b. Total energy in the circuit, U≈6.56J
- c. Energy stored in the inductor, UL≈0.56J
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Example Type 5
Explore 2 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Example Type 6
Explore 3 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Example Type 3
Explore 4 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Medical entrances gallery
Explore 97 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
Similar Questions
Find the charge and energy stored on the capacitor C in the following circuit.
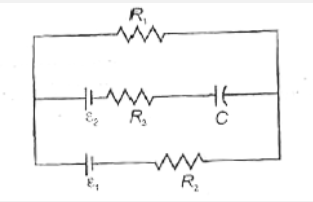
View SolutionFind total energy stored in capacitors given in the circuit
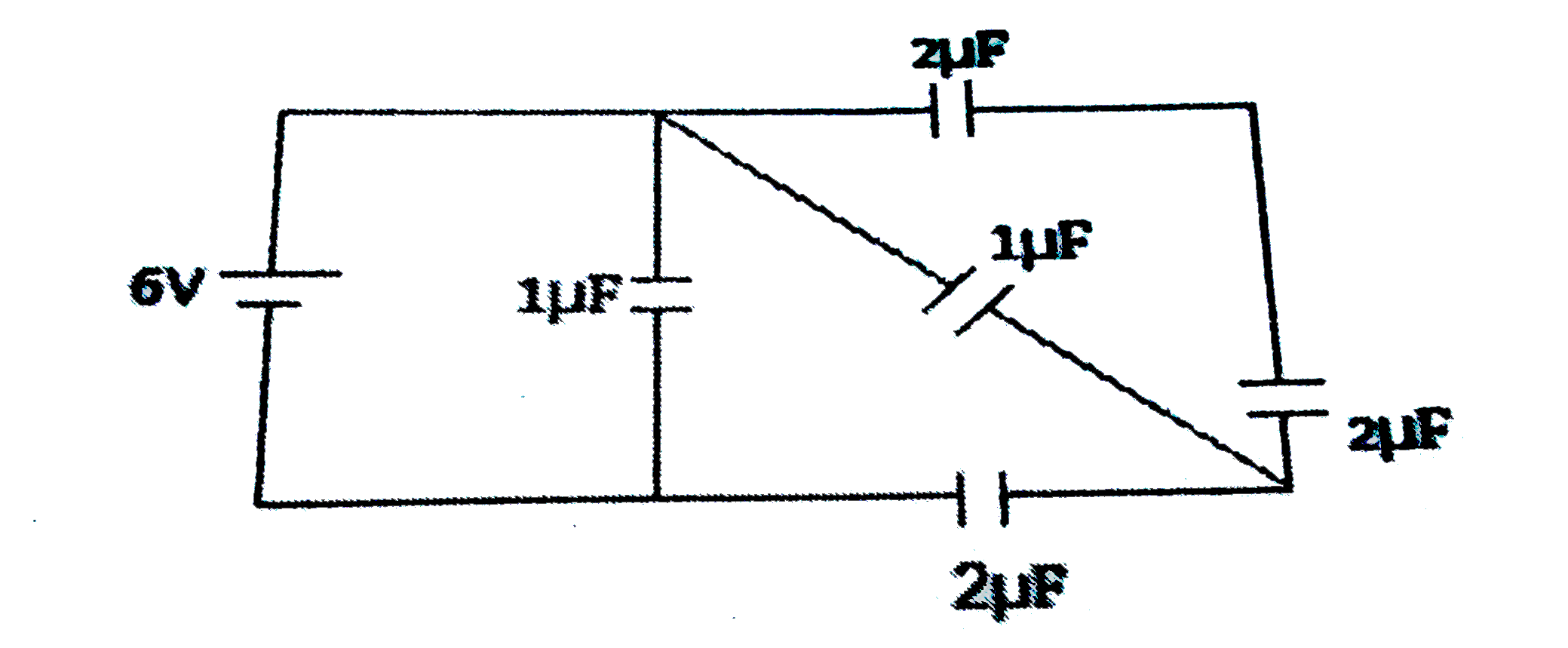
View SolutionThe energy stored in a capacitor of capacity C and potential V is given by
View Solutionwhat is the charge stored on each capacitor C1andC2 in the circuit shown in fig.
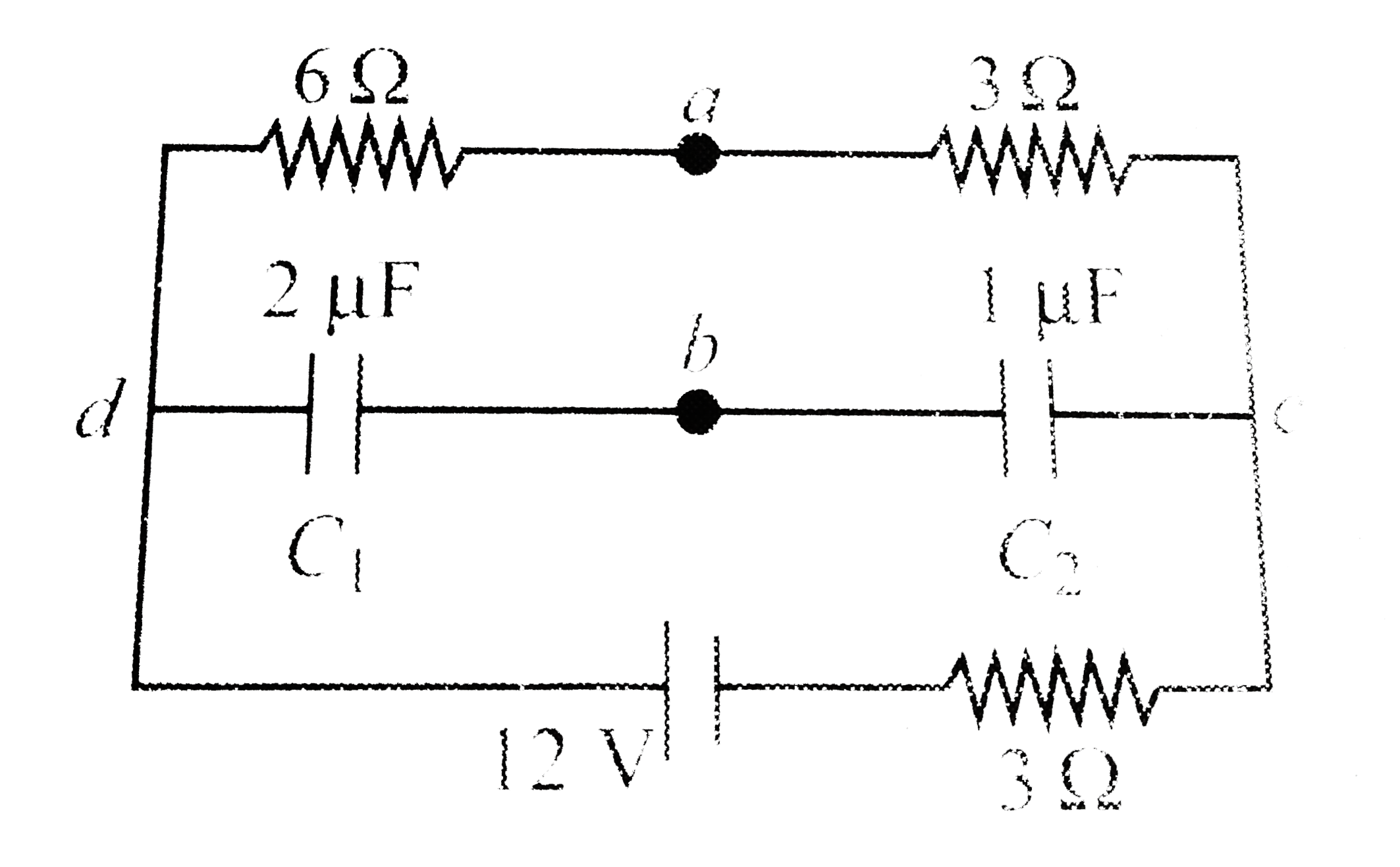
View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View SolutionIn the circuit what is the change of total electrical energy stored in the capacitors when the key is pressed ?
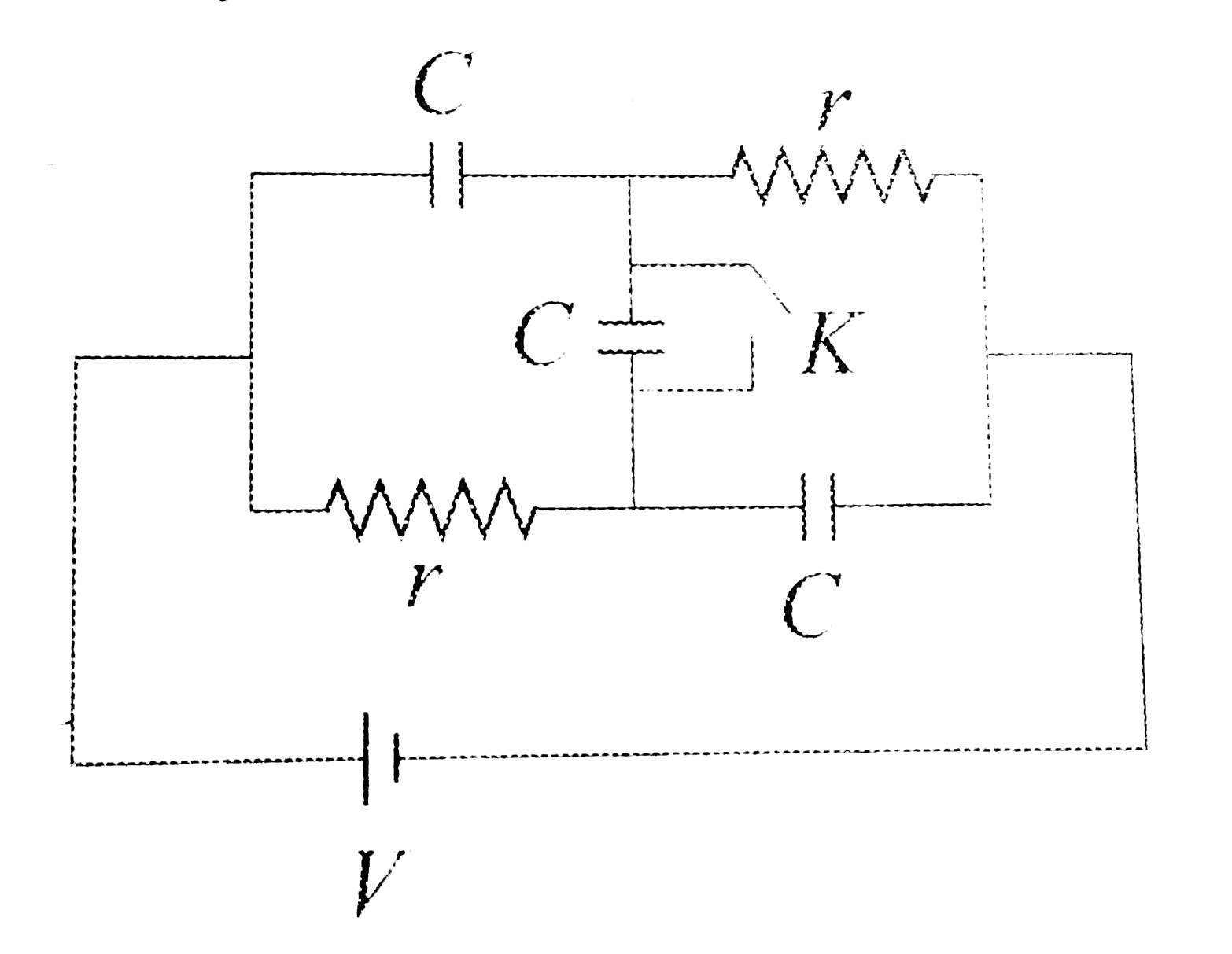
View SolutionConsider the given circuit.Initially there is no energy stored in inductor and capacitor.At
View SolutionConsider the given circuit.Initially there is no energy stored in inductor and capacitor.At
View SolutionIn the given at t=0, switch S is closed.
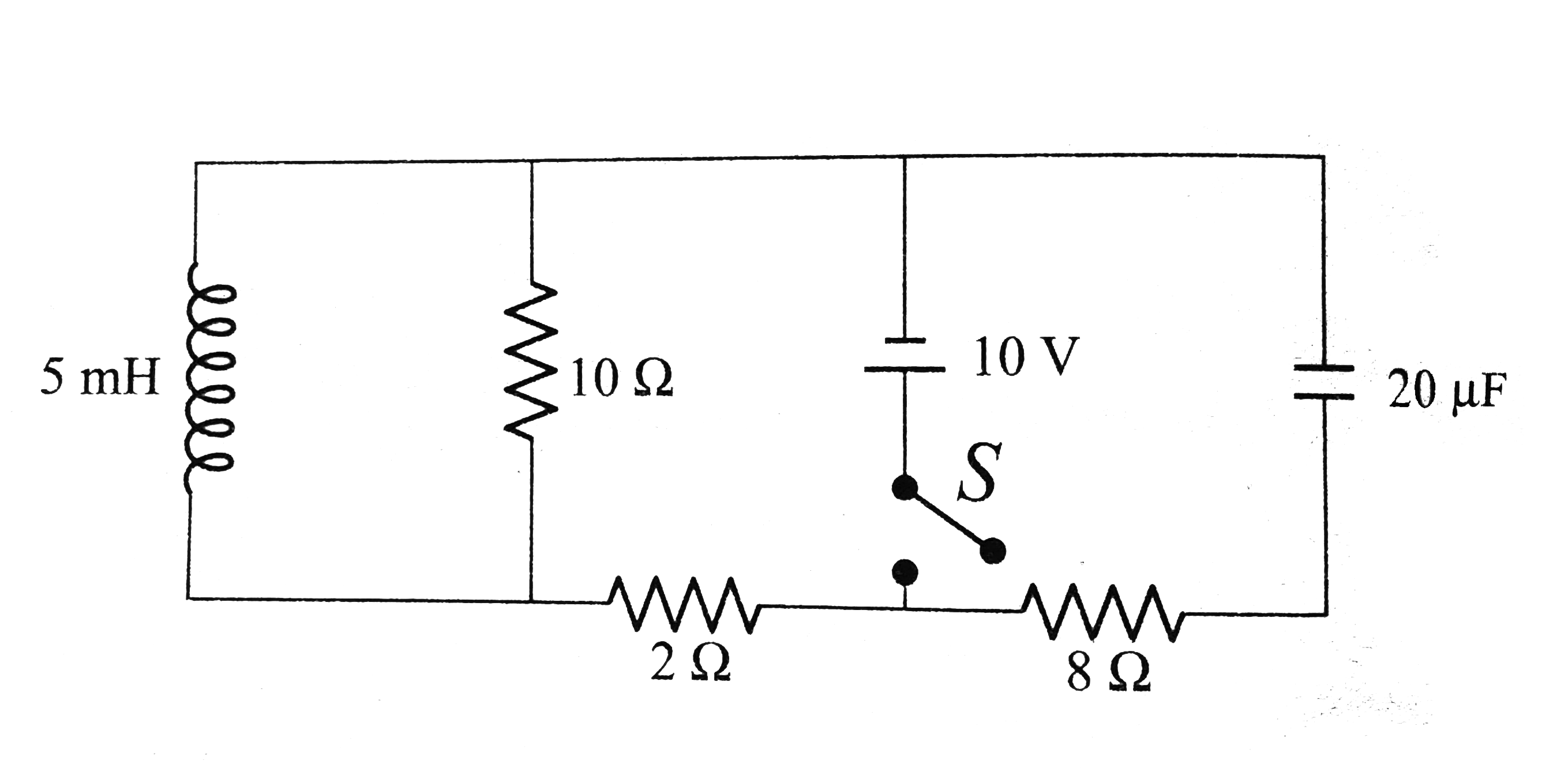
The energy stored in the capacitor and inductor, respectively, at t→∞ will be
View SolutionIn the circuit shown in figure 3.141, find the energy stored in 4μF capacitor in steady state.
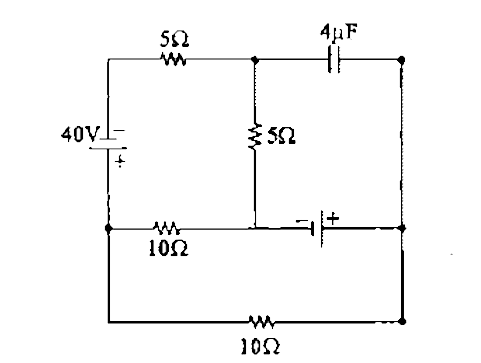
View Solution

