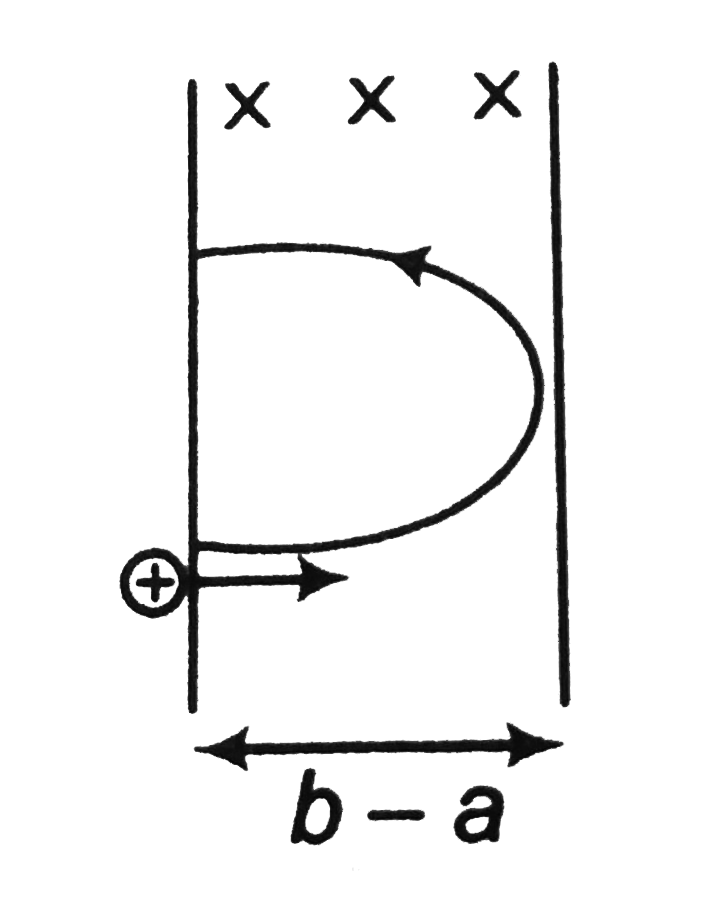
A particle of mass m and charge q moves with a constant velocity v along the positive x− direction. It enters a region containing a uniform magnetic field B directed along the negative z direction, extending from x=a to x=b. The minimum value of v required so that the particle can just enter the region x>b is

qBbm
qBam
qB(b−a)m
qB(b+a)2m
The correct Answer is:C
(b−a)= radius of circular part
=mvBq
∴V=Bq(b−a)m
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
A particle of mass m and charge q moves with a constant velocity v along the positive x direction. It enters a region containing a uniform magnetic field B directed along the negative z direction, extending from x=a to x=b. The minimum value of v required so that the particle can just enter the region x>b is
View SolutionA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
View SolutionA particle of charge q and mass m moving with a velocity v along the x-axis enters the region x>0 with uniform magnetic field B along the ˆk direction. The particle will penetrate in this region in the x-direction upto a distance d equal to
View SolutionA positively charged particle moving due east enters a region of uniform magnetic field directed vertically upwards. The partical will be
View SolutionA charged particle (charge q, mass m) has velocity v0 at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
View SolutionA charged particle of mass m and charge q is accelerated through a potential difference of V volts. It enters a region of uniform magnetic field which is directed perpendicular to the direction of motion of the particle. Find the radius of circular path moved by the particle in magnetic field.
View SolutionA particle of mass m carrying charge q is accelerated by a potential difference V. It enters perpendicularly in a region of uniform magnetic field B and executes circular arc of radius R, then qm equals
View SolutionA particle of mass m is moving with constant speed v on the line y=b in positive x-direction. Find its angular momentum about origin, when position coordinates of the particle are (a, b).
View SolutionA charged particle of mass m and charge q is accelerated through a potential differences of V volts. It enters of uniform magnetic field B which is directed perpendicular to the direction of motion of the particle. The particle will move on a circular path of radius
View SolutionA charged particle ( mass m and charge q) moves along X axis with velocity V0 . When it passes through the origin it enters a region having uniform electric field →E=−Eˆj which extends upto x=d . Equation of path of electron in the region . x>d is :

View Solution
