In a region of space, a uniform magnetic field B is along positive x-axis. Electrons are ernit.u.d from the origin with speed u at different, angles. Show that the paraxial electrons are refocused on the x-axis at a distance 2πmvBe. Here, m is the mass of electron and e the charge on it.
The correct Answer is:A
To solve the problem, we need to analyze the motion of electrons emitted from the origin in a uniform magnetic field directed along the positive x-axis. The goal is to show that paraxial electrons refocus on the x-axis at a distance of 2πmvBe.
1. Understanding the Setup:
- We have a uniform magnetic field B directed along the positive x-axis.
- Electrons are emitted from the origin with speed u at different angles θ.
2. Motion of Electrons in a Magnetic Field:
- When charged particles (like electrons) move in a magnetic field, they experience a magnetic force given by:
F=q(v×B)
- Here, q is the charge of the electron, v is the velocity vector of the electron, and B is the magnetic field vector.
3. Determining the Components of Velocity:
- The velocity u can be decomposed into components:
- ux=ucosθ (along the x-axis)
- uy=usinθ (along the y-axis)
4. Radius of Circular Motion:
- The electrons will undergo circular motion in the plane perpendicular to the magnetic field. The radius r of this circular motion is given by:
r=mveB
- Here, m is the mass of the electron, v is the speed of the electron, e is the charge of the electron, and B is the magnetic field strength.
5. Time Period of Circular Motion:
- The time period T for one complete revolution is given by:
T=2πmeB
6. Distance Traveled in the x-direction:
- The distance traveled along the x-axis during one complete revolution can be calculated as:
Distance=Velocity in x-direction×Time Period
- The velocity in the x-direction is ucosθ, so:
Distance=(ucosθ)×T=(ucosθ)×2πmeB
7. Focusing Condition for Paraxial Electrons:
- For paraxial electrons, we consider θ to be very small (close to zero). Thus, cosθ≈1.
- Therefore, the distance becomes:
Distance=u×2πmeB
8. Final Distance for Paraxial Electrons:
- Since we are interested in the distance where the electrons refocus on the x-axis, we can set u=v (the speed of the electrons):
Distance=2πmveB
Thus, we have shown that paraxial electrons are refocused on the x-axis at a distance 2πmveB.
- We have a uniform magnetic field B directed along the positive x-axis.
- Electrons are emitted from the origin with speed u at different angles θ.
- When charged particles (like electrons) move in a magnetic field, they experience a magnetic force given by:
F=q(v×B)
- Here, q is the charge of the electron, v is the velocity vector of the electron, and B is the magnetic field vector.
- The velocity u can be decomposed into components:
- ux=ucosθ (along the x-axis)
- uy=usinθ (along the y-axis)
- The electrons will undergo circular motion in the plane perpendicular to the magnetic field. The radius r of this circular motion is given by:
r=mveB
- Here, m is the mass of the electron, v is the speed of the electron, e is the charge of the electron, and B is the magnetic field strength.
- The time period T for one complete revolution is given by:
T=2πmeB
- The distance traveled along the x-axis during one complete revolution can be calculated as:
Distance=Velocity in x-direction×Time Period
- The velocity in the x-direction is ucosθ, so:
Distance=(ucosθ)×T=(ucosθ)×2πmeB
- For paraxial electrons, we consider θ to be very small (close to zero). Thus, cosθ≈1.
- Therefore, the distance becomes:
Distance=u×2πmeB
- Since we are interested in the distance where the electrons refocus on the x-axis, we can set u=v (the speed of the electrons):
Distance=2πmveB
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
In a region of space, a uniform magnetic field B exists in the x-direction. An electron is fired from the origin with its initial velocity u making an angle α with the y direction in the y-z plane. In the subsequent motion of the electron,

View SolutionConsider the following figure, a uniform magnetic field of 0.2 T is directed along the positive X-axis. The magnetic flux through top surface of the figure.
View Solution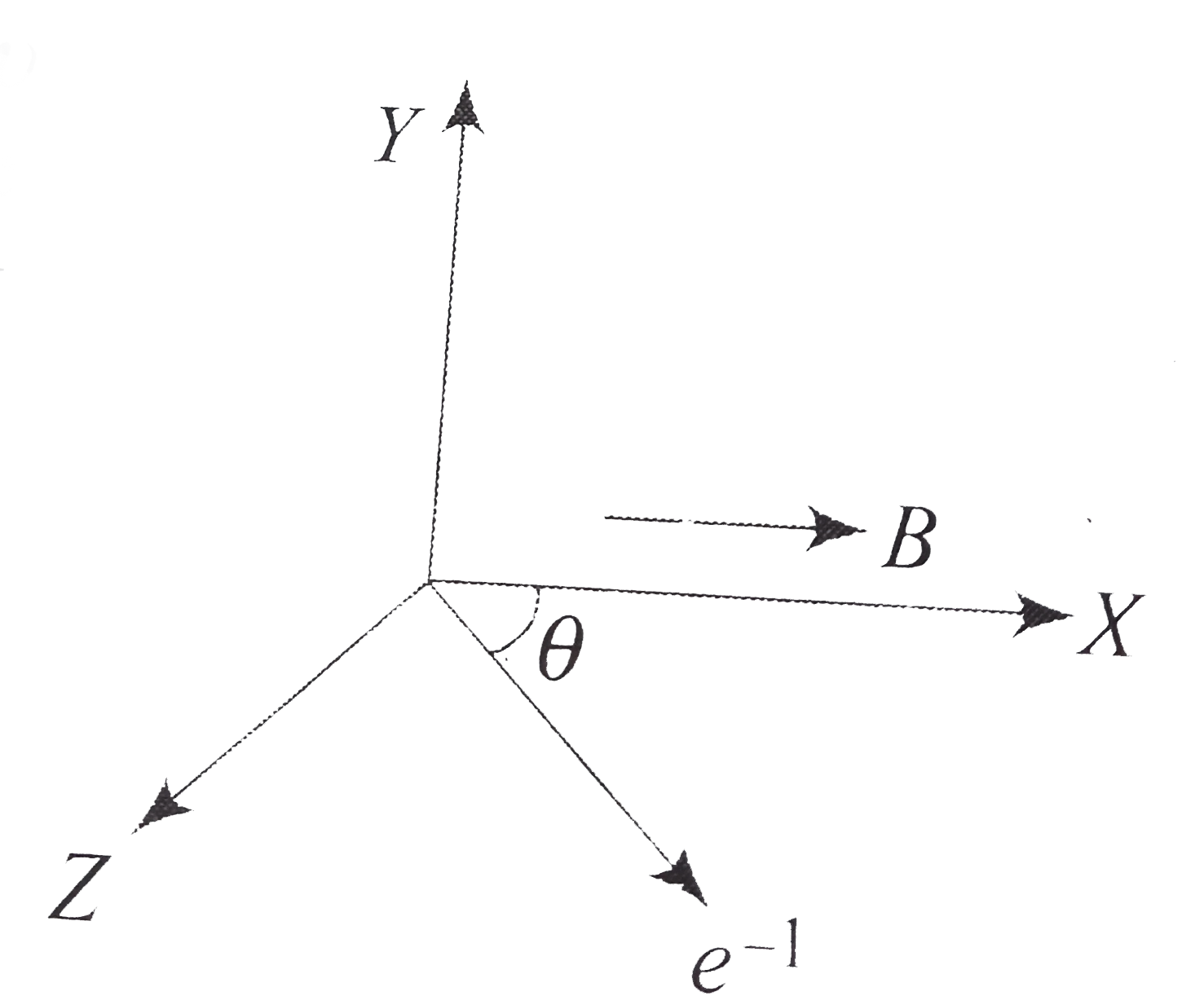
Light having photon energy hυ is incident on a metallic plate having work function ϕ to eject the electrons. The most energetic enectrons are then allowed to enter in a region of uniform magnetic field B as shown in Fig. The electrons are projected In X-Z plane making an angle θ with X-axis and magnetic field is →B=B0ˆi along X-axis maximum pitch of the helix described by an electron is found to be p. Take mass of electron as m and charge as q. Based on the above information, answer the following questions:
Q. The plot between X-coordinate of the location of electron as a function of time for different frequencies υ of the incident light is
View Solution
Light having photon energy hυ is incident on a metallic plate having work function ϕ to eject the electrons. The most energetic enectrons are then allowed to enter in a region of uniform magnetic field B as shown in Fig. The electrons are projected In X-Z plane making an angle θ with X-axis and magnetic field is →B=B0ˆi along X-axis maximum pitch of the helix described by an electron is found to be p. Take mass of electron as m and charge as q. Based on the above information, answer the following questions:
Q. Considering the instant of crossing origin at t=0 ,the Z-coordinate of the location of electron as a function of time is
View Solution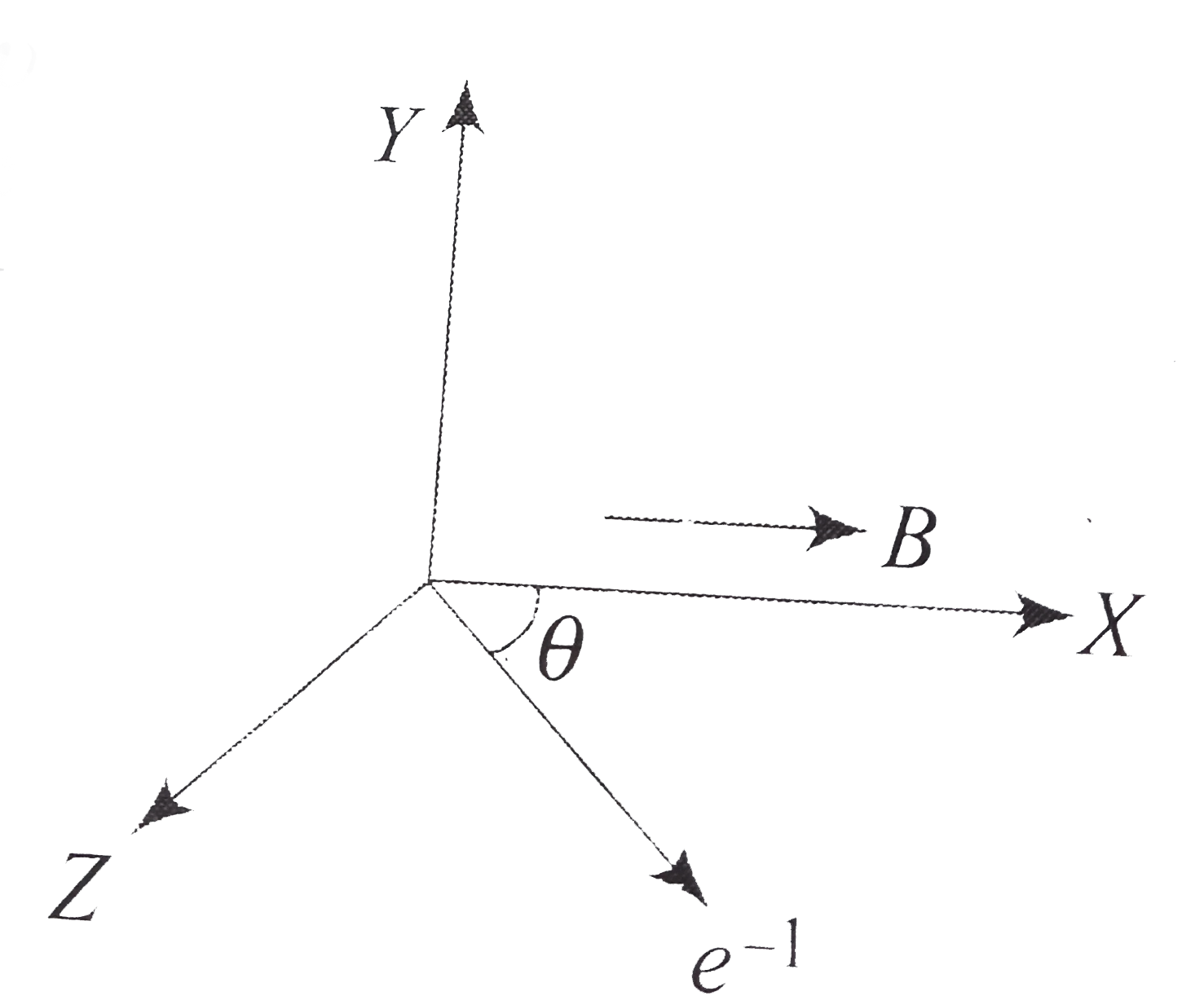
Light having photon energy hυ is incident on a metallic plate having work function ϕ to eject the electrons. The most energetic enectrons are then allowed to enter in a region of uniform magnetic field B as shown in Fig. The electrons are projected In X-Z plane making an angle θ with X-axis and magnetic field is →B=B0ˆi along X-axis maximum pitch of the helix described by an electron is found to be p. Take mass of electron as m and charge as q. Based on the above information, answer the following questions:
Q. The correct relation between p and B0 is
View SolutionIn a region of uniform electric field ofn intencity E, an electron of mass me is released from rest. The distance travelled by the eloctron in a time t is
View SolutionIn a region there exists a magnetic field B0 along positive x-axis. A metallic wire of length 2a, one side along x-axis and one side parallel of y-axis is rotates about y-axis with a angular velocity. Then at the instant shown

View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of 60∘ with the positive x-axis in x-y plane. When the x-coordinate of particle becomes √3mv2/qE a uniform and constant magnetic. field of strength B is also switched on along positive y-axis.
x-coordinate of the particle as a function of time after the magnetic field is switched on is
View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of 60∘ with the positive x-axis in x-y plane. When the x-coordinate of particle becomes √3mv2/qE a uniform and constant magnetic field of strength B is also switched on along positive y-axis.
Velocity of the particle just before the magnetic field is switched on is
View SolutionA uniform magnetic field exists in a circular region of radius r.The magnitude of magnetic field is B and points inward.An electron flies into the region radially as shown in figure.After a certain time, the electron deflected by the magnetic field leaves the region.The time interval during which the electron moves in the region is Nmtan−1eBrmVeB.Then find value of N.(m is mass of electron and e is charge of electron)
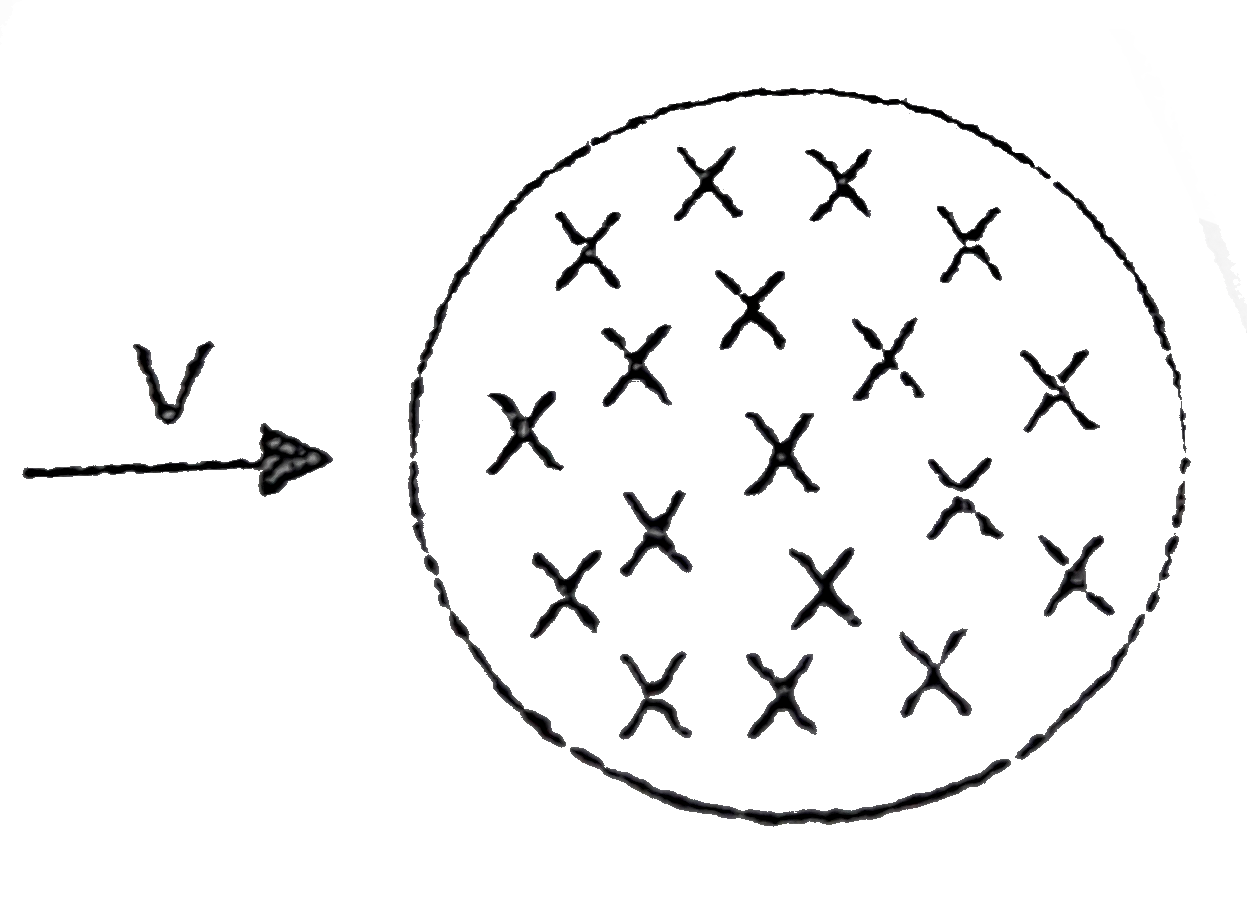
View Solution
