A charged particle enters a region of uniform magnetic field at an angle of 85∘ to the magnetic line of force. The path of the particle is a circle. Is this statement true or false?
To determine whether the statement "A charged particle enters a region of uniform magnetic field at an angle of 85 degrees to the magnetic line of force. The path of the particle is a circle" is true or false, we can analyze the motion of the charged particle in a magnetic field step by step.
1. Understanding the Motion of a Charged Particle in a Magnetic Field:
- A charged particle moving in a magnetic field experiences a magnetic force that is given by the equation:
→F=q(→v×→B)
- Here, →F is the magnetic force, q is the charge of the particle, →v is the velocity vector of the particle, and →B is the magnetic field vector.
2. Analyzing the Angle of Entry:
- The problem states that the particle enters the magnetic field at an angle of 85∘ to the magnetic field lines. This means that the angle between the velocity vector and the magnetic field vector is 85∘.
3. Breaking Down the Velocity Components:
- The velocity →v can be resolved into two components:
- Parallel to the Magnetic Field:
v∥=vcos(85∘)
- Perpendicular to the Magnetic Field:
v_{\perpendicular} = v \sin(85^\circ)
4. Effect of the Magnetic Force:
- The magnetic force acts only on the component of velocity that is perpendicular to the magnetic field. Thus, only the v_{\perpendicular} component will experience the magnetic force, which will cause the particle to move in a circular path.
- The component v∥ will not experience any force and will continue to move in the same direction.
5. Resulting Path of the Particle:
- Since the particle has a component of velocity parallel to the magnetic field, it will not only move in a circular path due to the perpendicular component but will also translate along the direction of the magnetic field.
- Therefore, the actual path of the particle will be a helix, not a circle.
6. Conclusion:
- The statement that the path of the particle is a circle is false. The correct path is a helical trajectory due to the combination of circular motion (from the perpendicular component) and linear motion (from the parallel component).
Final Answer:
The statement is false.
- A charged particle moving in a magnetic field experiences a magnetic force that is given by the equation:
→F=q(→v×→B)
- Here, →F is the magnetic force, q is the charge of the particle, →v is the velocity vector of the particle, and →B is the magnetic field vector.
- The problem states that the particle enters the magnetic field at an angle of 85∘ to the magnetic field lines. This means that the angle between the velocity vector and the magnetic field vector is 85∘.
- The velocity →v can be resolved into two components:
- Parallel to the Magnetic Field:
v∥=vcos(85∘)
- Perpendicular to the Magnetic Field:
v_{\perpendicular} = v \sin(85^\circ)
- The magnetic force acts only on the component of velocity that is perpendicular to the magnetic field. Thus, only the v_{\perpendicular} component will experience the magnetic force, which will cause the particle to move in a circular path.
- The component v∥ will not experience any force and will continue to move in the same direction.
- Since the particle has a component of velocity parallel to the magnetic field, it will not only move in a circular path due to the perpendicular component but will also translate along the direction of the magnetic field.
- Therefore, the actual path of the particle will be a helix, not a circle.
- The statement that the path of the particle is a circle is false. The correct path is a helical trajectory due to the combination of circular motion (from the perpendicular component) and linear motion (from the parallel component).
The statement is false.
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
When a charged particle enters a uniform magnetic field its kinetic energy
View SolutionIf a charged particle enters perpendicular in the uniform magnetic field then
View SolutionA charged particle enters a uniform magnetic field perpendicular to it. The magnetic field
View SolutionThe trajectory of a charged particle is the same as a field line. Is this statement true or false?
View SolutionA charged particle enters a unifrom magnetic field with velocity vector at an angle of 45∘ with the magnetic field . The pitch of the helical path followed by the particles is ρ . The radius of the helix will be
View SolutionA charged particle enters in a uniform magnetic field perpendicular to it. Now match the following two columns.

View SolutionA charged particle enters in a magnetic field B with its initial velocity making an angle of 45° with B. The path of the particle will be
View SolutionFour particles enter a region of uniform magnetic field. Their trajectories are shown in figure. What are the signs of the charge of all four particles ?
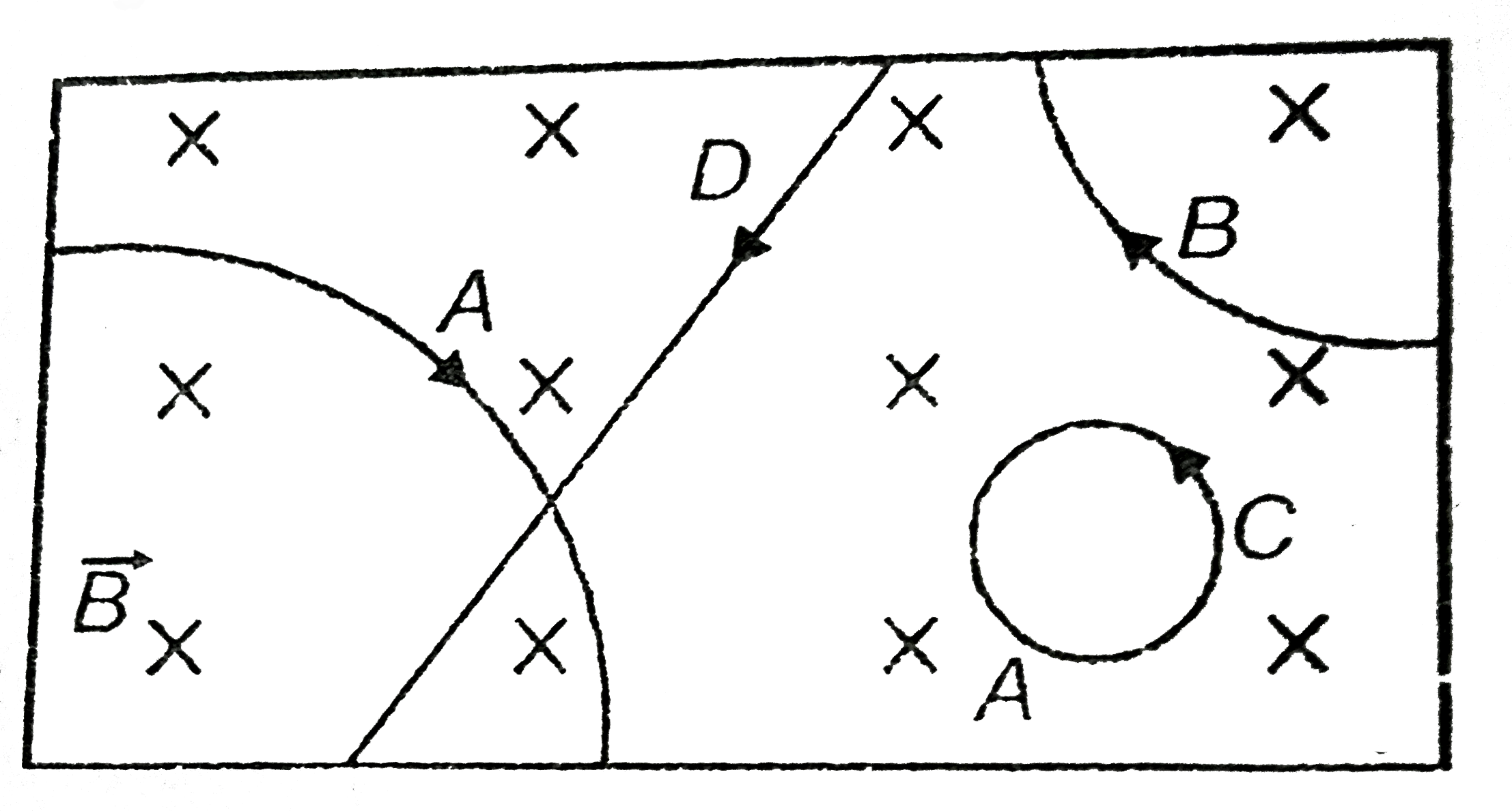
View SolutionIf a charged particle is a plane perpendicular to a uniform magnetic field with a time period T Then
View SolutionA charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be
View Solution
