A charged particle carrying charge q=1μc moves in uniform magnetic with velocity v1=106m/s at angle 45∘ with x-axis in the xy-plane and experiences a force F1=5√2N along the negative z-axis. When te same particle moves with velocity v2=106m/s along the z-axis it experiences a force F2 in y-direction. Find
a. the magnitude and direction of the magnetic field
b. the magnitude of the force F2.
To solve the problem, we will break it down into two parts: finding the magnitude and direction of the magnetic field (part a), and then calculating the magnitude of the force F2 (part b).
Part a: Finding the Magnitude and Direction of the Magnetic Field
1. Given Data:
- Charge of the particle, q=1μC=1×10−6C
- Velocity v1=106m/s at an angle of 45∘ with the x-axis in the xy-plane.
- Force F1=5√2N along the negative z-axis.
2. Velocity Components:
- The velocity can be broken down into components:
v1x=v1cos(45∘)=106×1√2=5×105m/s
v1y=v1sin(45∘)=106×1√2=5×105m/s
3. Direction of the Magnetic Field:
- The force F1 is in the negative z-direction. According to the right-hand rule for the cross product F=q(v×B), the magnetic field B must lie in the xy-plane.
4. Using the Force Equation:
- The force can be expressed as:
F1=q⋅v1⋅B⋅sin(θ)
- Here, θ is the angle between the velocity vector and the magnetic field. Since the velocity makes a 45∘ angle with the x-axis, the angle θ between v1 and B is also 45∘.
- Thus, we can write:
F1=q⋅v1⋅B⋅sin(45∘)
5√2=(1×10−6)⋅(106)⋅B⋅1√2
5. Solving for B:
- Rearranging gives:
5√2=10−6⋅106⋅B⋅1√2
5√2=B⋅1√2
B=5√2⋅√2=10T
6. Direction of B:
- Since the force is in the negative z-direction and the particle moves in the xy-plane, the magnetic field B is directed along the positive x-axis.
- Therefore, we can express the magnetic field as:
B=10^iT
Part b: Finding the Magnitude of the Force F2
1. Given Data for Part b:
- The particle moves with velocity v2=106m/s along the z-axis.
- The magnetic field B=10^iT.
2. Using the Force Equation:
- The force can be expressed as:
F2=q⋅v2⋅B⋅sin(θ)
- Here, the angle θ between v2 (which is along the z-axis) and B (which is along the x-axis) is 90∘.
3. Calculating F2:
- Thus, we have:
F2=(1×10−6)⋅(106)⋅(10)⋅sin(90∘)
F2=(1×10−6)⋅(106)⋅(10)⋅1
F2=10N
4. Direction of F2:
- Since the force F2 is in the y-direction, we can express it as:
F2=10^jN
Final Answers:
- Part a: The magnitude of the magnetic field is 10T in the direction of the positive x-axis.
- Part b: The magnitude of the force F2 is 10N in the direction of the positive y-axis.
- Charge of the particle, q=1μC=1×10−6C
- Velocity v1=106m/s at an angle of 45∘ with the x-axis in the xy-plane.
- Force F1=5√2N along the negative z-axis.
- The velocity can be broken down into components:
v1x=v1cos(45∘)=106×1√2=5×105m/s
v1y=v1sin(45∘)=106×1√2=5×105m/s
- The force F1 is in the negative z-direction. According to the right-hand rule for the cross product F=q(v×B), the magnetic field B must lie in the xy-plane.
- The force can be expressed as:
F1=q⋅v1⋅B⋅sin(θ)
- Here, θ is the angle between the velocity vector and the magnetic field. Since the velocity makes a 45∘ angle with the x-axis, the angle θ between v1 and B is also 45∘.
- Thus, we can write:
F1=q⋅v1⋅B⋅sin(45∘)
5√2=(1×10−6)⋅(106)⋅B⋅1√2
- Rearranging gives:
5√2=10−6⋅106⋅B⋅1√2
5√2=B⋅1√2
B=5√2⋅√2=10T
- Since the force is in the negative z-direction and the particle moves in the xy-plane, the magnetic field B is directed along the positive x-axis.
- Therefore, we can express the magnetic field as:
B=10^iT
- The particle moves with velocity v2=106m/s along the z-axis.
- The magnetic field B=10^iT.
- The force can be expressed as:
F2=q⋅v2⋅B⋅sin(θ)
- Here, the angle θ between v2 (which is along the z-axis) and B (which is along the x-axis) is 90∘.
- Thus, we have:
F2=(1×10−6)⋅(106)⋅(10)⋅sin(90∘)
F2=(1×10−6)⋅(106)⋅(10)⋅1
F2=10N
- Since the force F2 is in the y-direction, we can express it as:
F2=10^jN
- Part a: The magnitude of the magnetic field is 10T in the direction of the positive x-axis.
- Part b: The magnitude of the force F2 is 10N in the direction of the positive y-axis.
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
A charged particle carrying charge q=10μC moves with velocity v1=106ms−1 at angle 45∘ with x-axis in the xy plane and experience a force F1=5√2mN along the negative z-axis. When the same particle moves with velocity v2=106ms−1 along the z-axis, it experiences a force F2 in y-direction.
Find the magnitude of the force F2.
View SolutionA charged particle carrying charge q=10μC moves with velocity v1=106,s−1 at angle 45∘ with x-axis in the xy plane and experience a force F1=5√2mN along the negative z-axis. When the same particle moves with velocity v2=106ms−1 along the z-axis, it experiences a force F2 in y-direction.
Find the magnetic field →B.
View SolutionA beam of α particles projected along + x-axis, experiences a force due to a magnetic field along the +y-axis figure. What is the direction of magnetic field.
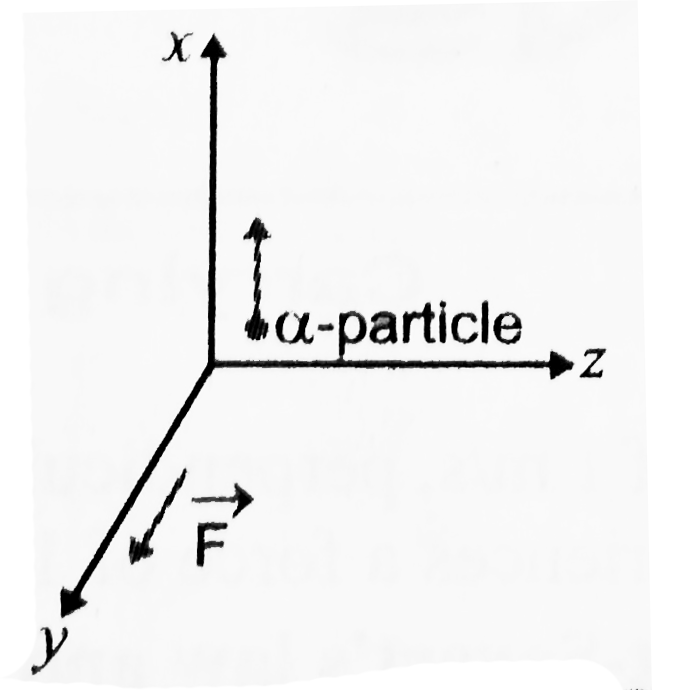
View SolutionA charge q is moving with a velocity v1=1ˆi m/s at a point in a magentic field and experiences a force F=q[−ˆj+1ˆk] N. If the charge is moving with a voloctiy v2=ˆj m/s at the same point then it experiences a force F2=q(1ˆi−1ˆk) N. The magnetic induction B at that point is
View SolutionA particle of charge −16×10−18 coulomb moving with velocity 10ms−1 along the x− axis , and an electric field of magnitude 104/(m) is along the negative z− axis. If the charged particle continues moving along the x- axis , the magnitude of B is
View SolutionWhen a proton has a velocity v=(2ˆi+3ˆj)×106ms, it experience a force F=−(1.28×10−13ˆk) When its velocity is along the z-axis, it experience a force along the x-axis. What is the magnetic field?
View SolutionWhen as proton has a velocity v=(2ˆi+3ˆj)×106ms, it experience a force F=−(1.28×10−13ˆk) When its velocity is along the z-axis, it experience a force along the x-axis. What is the magnetic field?
View SolutionA particle of charge −16×10−18 coo–mb moving with velocity 10ms−1 along the x−aξs, and an electric field of magnitude (104)/(m) is along the negative z−ais. If the charged particle continues moving along the x- axis , the magnitude of B is
View SolutionA charge q moves with a velocity 2m/s along x- axis in a unifrom magnetic field B=(ˆi+2ˆj+3ˆk) tesla.
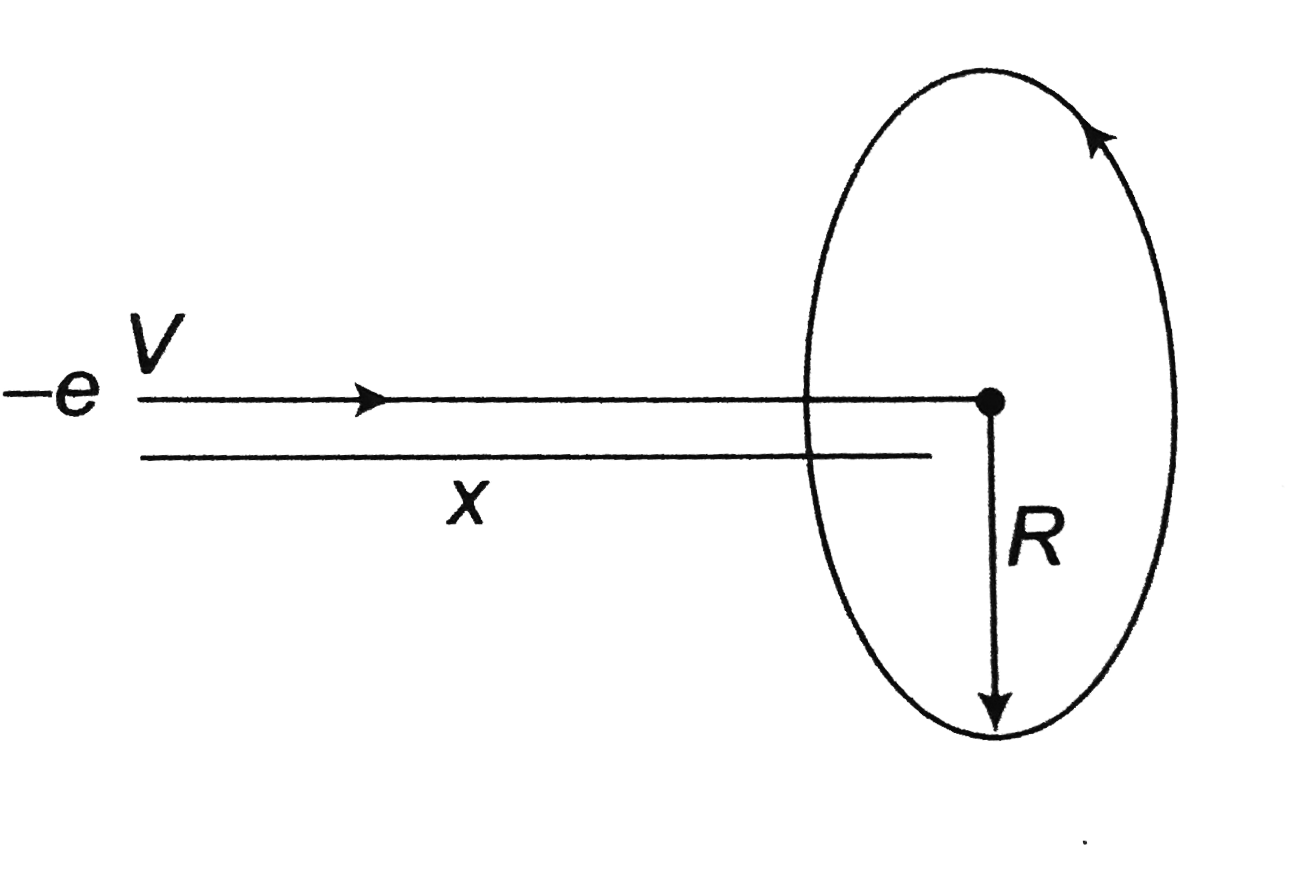
View SolutionAn electron moving with a velocity v along the positive x-axis approaches a circular current carrying loop as shown in the fig. the magnitude of magnetic force on electron at this instant is
View Solution
