When E⊥B and the particle is released at rest from origin.
Consider a particle of charge q and mass m emitted at origin with zero initial velocity into a regionof uniform electric and magnetic fields. The field E is acting along x-axis and field B along y=axis, i.e.
E=E0ˆj
and B=B0ˆj
Electric fiedl will provide the particle an acceleration (and therefore a velocity component O) in x-direction and the magnetic field will rotate the particle in xy-plane (perpendicular to B).
Hence, at any instant of time its velocity (and hence, position) will have only x and y components. Let at time t its veloicty be
v=vxˆi+vzˆk
Net force on it at this instant is
F=Fe+Fm=qE+q(v×B)
=q[E0ˆi+(vξ+vzˆk)×(B0ˆj)]
or F=q(E0−vzB0)ˆi+qvxB0ˆk
∴a=Fm=axˆi+azˆk
whereax=qm(E0−vzB0) .............i
and azqmvxB0 ..........ii
Differenting eqn i w.r.t time we have
d2vxdt2=qB0m(dvzdt)
But, dvzdt=az=qB0mvx
∴d2vxdt2=−(qB0m)2vx........iii
comparing this equation with the differential equation of SHM (d2y(dt)2=−ω2y), we get
ω=qB0m
and the general solution of eq. iii is
vx=(Asin(ωt+ϕ)........iv
At time t=0,vx=0, hence ϕ=0
Again dvxdt=Aωcosωt)(asϕ=0)
From eqn i axqE0matt=0,asvz=0att=0
∴Aω=qE0morA=qE0ωm
Substituting ω=qB0m, we get A=E0B0
Therefore eq. iv becomes
where vx=E0B0sinωt
ω=qB0m
Now substituting value of vx in eqn ii we get
dvzdt=qE0misnωt
∴∫v0_zdvz=qE0m∫t)sinωtdt
orvz=qE0ωm(1−cosωt)
Substituting ω=qB0m , we get
vz=E0B0(1−cosωt)
on integrating equation for v_x and u_z and knowng that at t=0,x=0 and z=0 we get
x=E0B0ω(1−cosωt)
z=E0B0ω(ωt−sinωt)
These eqution are the equation for a cycloid which is defined as the path generated by the point on the circumference of a wheel rolling on a ground.

In the present case, the radius of the rolling wheel is E0B0ω the maximum displacement along x- direction is 2E0B0ω. The x-displacement becomes zero at t=9, 2πω,4πω, etc.
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
If magnetic field in space is 1Tˆi, electric field is 10N/Cˆi, no gravitational field is present and a charged particle is released from rest from origin, it will
View SolutionLet A, B and C be points in a vertical line at height h, 4h5andh5 and from the ground. A particle released from rest from the point A reaches the ground in time T. The time taken by the particle to go from B to C is TBC . Then T(TBC)2=
View Solution
Knowledge Check
A positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge.
Aremains a constant because the electric field is uniform.Bincreases because the charge moves along the electric field.Cdecreases because the charge moves along the electric field.Ddecreases because the charge moves opposite to the electric field.A particle is released from rest from a tower of height 3h. The ratio of time intervals for fall of equal height h i.e. t1:t2:t3 is :
At1:t2:t3=3:2:1Bt1:t2:t3=1:(√2−1):(√3−2)Ct1:t2:t3=√3:√2:1Dt1:t2:t3=1:(√2−1):(√3−√2)
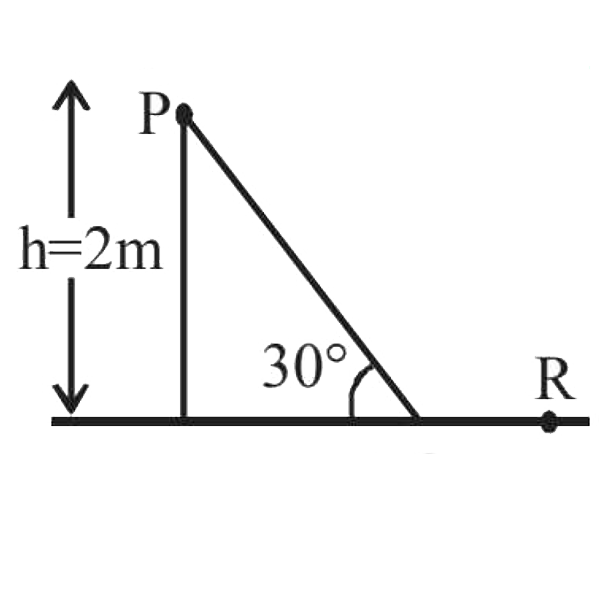
A point particle of mass m, moves long the uniformly rough track PQR as shown in figure. The coefficient of friction, between the particle and the rough track equals μ. The particle is released, from rest from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR.
The value of the coefficient of friction μ and the distance x (=QR), are, respectively close to:
View SolutionA proton is fixed at origin. Another proton is released from rest, from a point at a distance r from origin. Taking charge of portion as e and mass as m, find the speed of the proton (i) at a distance 2r from origin (ii) at large distance from origin.
View SolutionA positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge.
View SolutionA positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge.
View SolutionA particle is released from rest from a tower of height 3h. The ratio of time intervals for fall of equal height h i.e. t1:t2:t3 is :
View SolutionIn a region, steady and uniform electric and magnetic fields are present . These two fields are parallel to each other. A charged particle is released from rest in this region . The path of the particle will be a
View Solution
