A charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius a. (a) Find the surface charge density on the inner surface and on the outer surface. (b) If a charge q is put on the sphere, what would be the surface charge densities on the inner and the outer surface? (c) Find the electric field inside the sphere at a distance x from the centre in the situations (a) and (b).
The correct Answer is:A, B, C, D
To solve the problem step by step, we will address each part of the question systematically.
Part (a): Surface Charge Density on Inner and Outer Surfaces
1. Understanding the Setup: We have a hollow metallic sphere of radius a with a charge Q placed at its center. The sphere is initially uncharged.
2. Induced Charges: Since the charge Q is placed at the center, it will induce a charge of −Q on the inner surface of the sphere. This is because the electric field inside a conductor in electrostatic equilibrium must be zero.
3. Charge on the Outer Surface: The total charge of the sphere must remain zero (since it was initially uncharged). Therefore, the outer surface must have a charge of +Q to balance the −Q on the inner surface.
4. Calculating Surface Charge Densities:
- Inner Surface Charge Density (σinner):
σinner=−QAinner=−Q4πa2
- Outer Surface Charge Density (σouter):
σouter=QAouter=Q4πa2
Part (b): Surface Charge Densities with Charge q on the Sphere
1. Adding Charge q: When a charge q is placed on the outer surface of the sphere, the total charge on the outer surface becomes Q+q.
2. Inner Surface Charge Density: The inner surface charge density remains the same as before because the electric field inside the hollow sphere is still zero. Thus:
σinner=−Q4πa2
3. Outer Surface Charge Density:
σouter=Q+q4πa2
Part (c): Electric Field Inside the Sphere at Distance x
1. Electric Field in Situation (a):
- Inside the hollow metallic sphere, the electric field is zero because of the properties of conductors in electrostatic equilibrium.
Einside=0(for situation (a))
2. Electric Field in Situation (b):
- Similarly, since the charge Q is at the center and the electric field inside a conductor is always zero, the electric field remains zero.
Einside=0(for situation (b))
Summary of Answers:
- (a):
- Inner Surface Charge Density: σinner=−Q4πa2
- Outer Surface Charge Density: σouter=Q4πa2
- (b):
- Inner Surface Charge Density: σinner=−Q4πa2
- Outer Surface Charge Density: σouter=Q+q4πa2
- (c):
- Electric Field Inside Sphere: E=0 (for both situations (a) and (b))
- Inner Surface Charge Density (σinner):
σinner=−QAinner=−Q4πa2
- Outer Surface Charge Density (σouter):
σouter=QAouter=Q4πa2
σinner=−Q4πa2
σouter=Q+q4πa2
- Inside the hollow metallic sphere, the electric field is zero because of the properties of conductors in electrostatic equilibrium.
Einside=0(for situation (a))
- Similarly, since the charge Q is at the center and the electric field inside a conductor is always zero, the electric field remains zero.
Einside=0(for situation (b))
- (a):
- Inner Surface Charge Density: σinner=−Q4πa2
- Outer Surface Charge Density: σouter=Q4πa2
- Inner Surface Charge Density: σinner=−Q4πa2
- Outer Surface Charge Density: σouter=Q+q4πa2
- Electric Field Inside Sphere: E=0 (for both situations (a) and (b))
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE6videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.110videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Objective82videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
A charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius alpha. (a) Find the surface charge density on the inner surface and on the outer surface. (b) If a charge q is put on the sphere, what would be the surface charge densities on the inner and the outer surface?
View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View Solution
Knowledge Check
- Question 1 - Select One
In the question number 78, the surface charge density on the outer surface is
A−q4πR21Bq4πR22Cq24πR21D2q4πR22 - Question 2 - Select One
Two metal spheres, one fo radius R and the other of radius 2R, both have same surface charge density s. They are brought in contact and seprated. What will be new surface charge densitites on them ?
A52σ,54σB53σ,56σC35σ,65σD23σ,12σ
Charge density of the given surface is s. Then electric field stranght at the centre (of quarter sphere) is
 View Solution
View SolutionA metal spherical shell has an inner radius R1 and outer radius R2. A charge Q is placed at the center of the spherical cavity. What will be surface charge density on (i) the inner surface, and (ii) the outer surface ?
View SolutionA charge 'Q' is placed at the centre of a hemispherical surface of radius 'R'. The flux of electric field due to charge 'Q' through the surface of hemisphere is
View SolutionTwo metal spheres, one fo radius R and the other of radius 2R, both have same surface charge density s. They are brought in contact and seprated. What will be new surface charge densitites on them ?
View SolutionA metallic spherical shell has an inner radius R1 and outer radius R2. A charge is placed at the centre of the spherical cavity. The surface charge density on the inner surface is
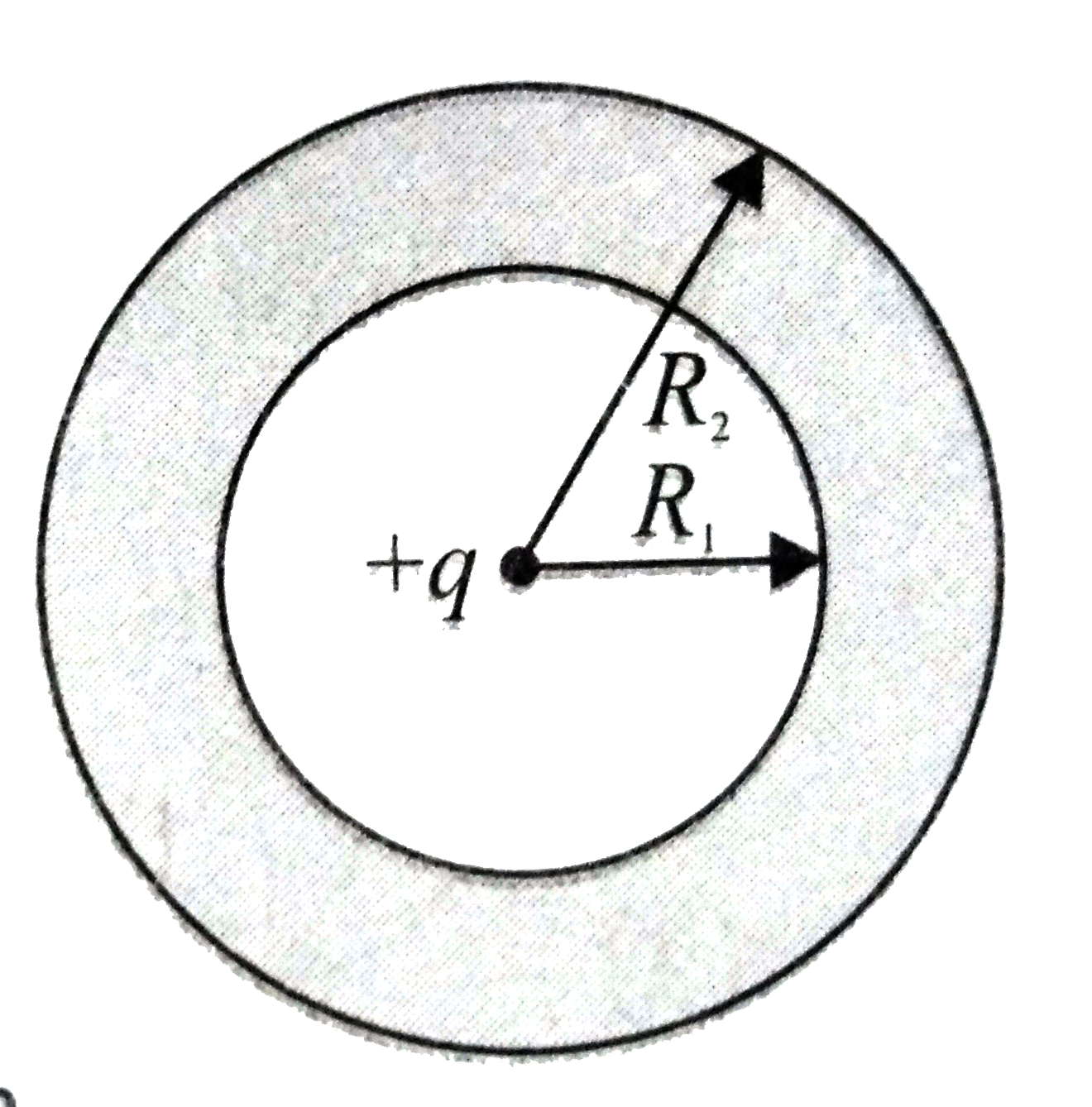 View Solution
View SolutionA point charge +Q is placed at the centre of an uncharged spherical conducting shell of inner radius a and outer radius b.
i. Find the electric field for r<a.
ii. What is the magnitude and sigh of the induced charge q' on the inner shell surface?
iii. What is the electric field at points r>b?
iv. What id the surface charge on the outer surface of the conductor?View Solution
